
Глава 12
12.1. Установим сначала свойства преобразования при операциях симметрии водородных 1s-орбиталей и углеводородных 2s- и 2р-орбиталей. Направим ось z по оси С3. Вычислим характеры представлений, базисами которых являются эти орбитали (см. задачу 8.5).

Заметим, что при повороте С3 2рх- и 2ру-орбитали переходят в линейные комбинации их. Соответствующая операции С3 матрица представления второго порядка выписана на стр. 136, а след ее равен - 1. Углеродная 2s-орбиталь будет давать МО с комбинацией водородных орбиталей симметрии А1', что приведет к образованию связывающей и разрыхляющей МО симметрии А1'. Аналогично 2рх- и 2рy-орбитали и комбинация водородных орбиталей с симметрией Е' будут давать связывающую и разрыхляющую МО симметрии Е'. Орбиталь 2рz - несвязывающая. Метильный радикал имеет семь электронов (не считая 1s-электронов атома углерода); шесть из них будут заполнять связывающие МО, а седьмой займет несвязывающую орбиталь.
Основному состоянию соответствует конфигурация (А1')2 (Е')4 (А2"), обладающая симметрией А2". Разрыхляющие орбитали имеют симметрию А1' и Е', и возбуждение электрона с А1'-связывающей на А1'-разрыхляющую орбиталь или с Е'-связывающей на Е'-разрыхляющую орбиталь также даст состояние с симметрией А2". Поэтому существует две одновозбужденных конфигурации, имеющие ту же симметрию, что и основное состояние.
Если молекула искажается и группой ее симметрии становится группа C3υ (в табл. 8.6 приведены характеры этой группы), то орбитали А1' и А2" имеют одинаковую симметрию А1 группы с более низкой симметрией; Е'-орбитали остаются двукратно вырожденными орбиталями симметрии Е группы С3υ. Поэтому искажение будет вносить примесь 2рz-орбитали в С - Н-связывающую молекулярную орбиталь симметрии A1 и увеличивать ее энергию; в несвязывающую же орбиталь будет вноситься примесь 2s-функции, что понизит ее энергию.
12.2. Три эквивалентные орбитали есть ортогональные линейные комбинации функций ψ1, ψ2 и ψ3. Свойства эквивалентных орбиталей преобразовываться друг через друга при операциях группы достаточны для того, чтобы определить коэффициенты этих линейных комбинаций точно таким же образом, как это было сделано при использовании симметрии для построения sр2-гибридных орбиталей (стр. 73). Вид sр2-гибридов можно фактически использовать как простой способ объяснения эквивалентных орбиталей.
Три sp2-гибридные функции имеют вид [см. уравнения (5.8-5.10)]:
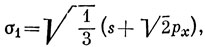
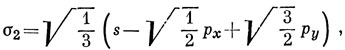
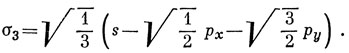
Функции ψ1, ψ2, ψ3. характеризуются теми же свойствами симметрии, что и s-, рх- и рy-орбитали соответственно. Отсюда следует, что тремя эквивалентными орбиталями являются
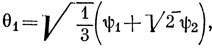
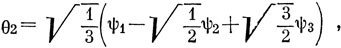
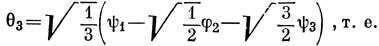
θ1 = 0,44 2s + 0,09 2pz + 0,51 2px + 0,42 h1 - 0,07 h2 - 0,07 h3,
θ2 = 0,44 2s + 0,09 2pz - 0,25 2px + 0,44 2py + 0,42 h2 - 0,07 h1 - 0,07 h3,
θ3 = 0,44 2s + 0,09 2pz - 0,25 2px - 0,44 2py + 0,42 h3 - 0,07 h1 - 0,07 h2.
12.3. Энергия структуры (а) (рис. (12.7) в приближении полного спаривания дается выражением [см. соотношение (12.31)]
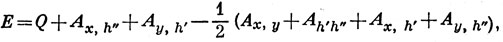
где А - обменные интегралы метода ВС, определенные в уравнении (11.11), х и у - кислородные 2рх- и 2ру-орбитали и h', h" - две водородные 1s-орбитали.
12.4. Сначала построим sp-гибридные функции [см. соотношение (5.4)] из АО бериллия:
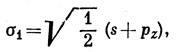
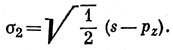
Тогда волновая функция молекулы ВеН2, построенная по методу ВС (см. задачу 11.3) имеет вид
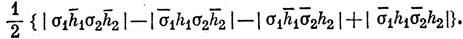
Валентному состоянию атома Be соответствует волновая функция
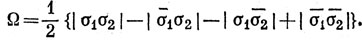
Выражая ее через АО и помня, что определители типа |ss| равны нулю, так как в них совпадают два столбца, имеем
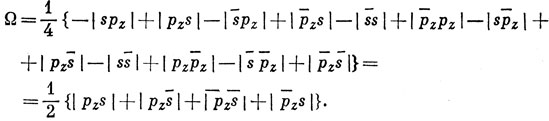
Все эти функции возникают из конфигурации 2s 2p атома Be, для которой возможны термы 1Р и 3Р. Первые два определителя описывают состояния со спинами +1 и -1 соответственно, и поэтому должны быть компонентами триплетного состояния. Третий определитель есть сумма синглетной и триплетной функций с Ms = 0:
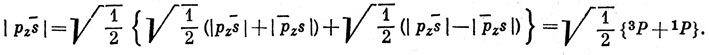
Аналогично последний определитель есть
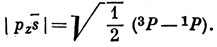
Для того чтобы получить функцию валентного состояния, суммируем квадраты коэффициентов при отдельных функциях атомного состояния. Тогда получим
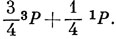
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'