Глава 11

11.1.

Аналогичное вычисление показывает, что функция Ψ_- также нормирована.

11.2. Рис. 19.9.

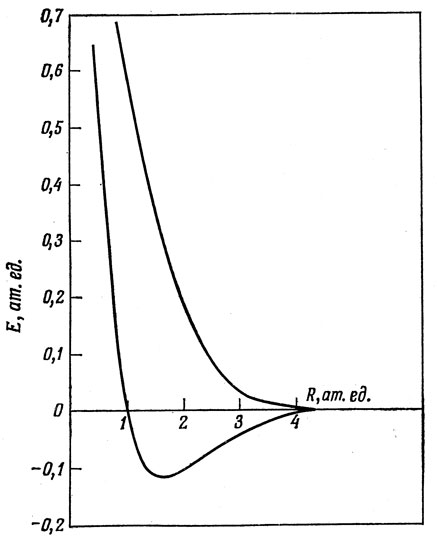
Рис. 19.9

11.3. Атом углерода имеет в основном состоянии конфигурацию (1s)² (2s)² (2р)². Можно ожидать, что два 2р-электрона дадут одну σ- и одну π-связи, но это привело бы к состоянию ¹Π; однако известно, что основным состоянием молекулы С₂ является состояние ¹∑_g⁺ (см. табл. 10.2). В методе МО основное состояние молекулы С₂ имеет заполненную оболочку π_u2р, а в методе ВС этому соответствовало бы образование π-связей обоими 2р-электронами. Используя те же обозначения, которые были приняты для молекулы N₂, получим волновую функцию

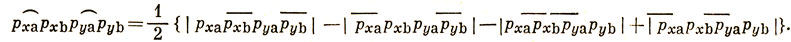
11.4. При допущении (а), нормировочная постоянная волновой функции Ψ есть

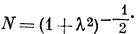
Дипольный момент получается обобщением выражения (10.51).

Пусть μ - оператор дипольного момента:

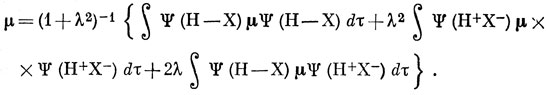
Из допущений (б) и (в) и условия ортогональности следует, что первое и последнее слагаемые равны нулю, поэтому

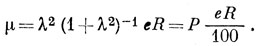
в силу допущения (в)

На основе приведенных в условии задачи данных строим следующую таблицу:

а) Волновые функции всегда можно выбрать нормированными но если они построены обычным способом из неортогональных АО [см. выражения (11.30), (11.31)], то они не будут ортогональны.

б) Это верно не всегда (см. рис. 11.4).

в) Если электронное облако атома X сферически симметрично, то дипольный момент молекулы Н + Х^- равен точно eR (на самом деле, это допущение справедливо, если электронное облако Х^- имеет центр симметрии, что легко можно видеть, если начало отсчета электронных и ядерных координат поместить в ядро X).

г) Это неверно, если волновые функции не ортогональны, и не обязательно верно, даже если они ортогональны. Интеграл с необходимостью обращается в нуль только в том случае, если электронные плотности Н и X^- не перекрываются ни в одной точке.

11.5. Уравнения для орбитальных коэффициентов имеют вид

Подставляя значения интегралов, получаем вековое уравнение

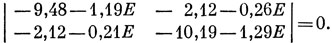
Решения его таковы: Е = - 7,882, Е = - 7,863. Подставляя низшее значение энергии в систему уравнений, находим

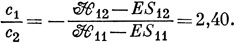
Тогда волновая функция основного состояния равна

Для того чтобы функция была нормированной, необходимо, чтобы

следовательно, N = 0,326 и Ψ = 0,782 Ψ₁ + 0,326 Ψ₂. Сравните ее с функцией на стр. 272.