Глава 10

10.1. Из выражения (10.16)

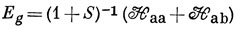
имеем

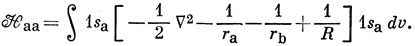
Но

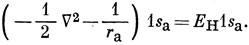
Следовательно,

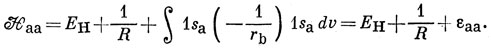
Аналогично

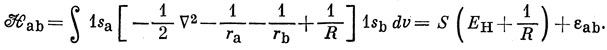
Значит,

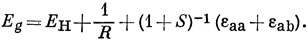
Подобным образом можно получить выражение (10.19) для энергии состояния ψ_u.

10.2. Согласно выражению (10.11), интеграл перекрывания между двумя 1s-орбиталями, центры которых расположены на расстоянии 2 ат. ед., равен 0,59.

Пусть 1s-орбитали имеют вид [см. выражение (10.10)]

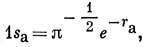
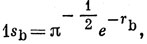
тогда

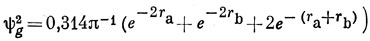
и

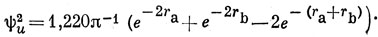
Эти функции показаны на рис. 19.7.

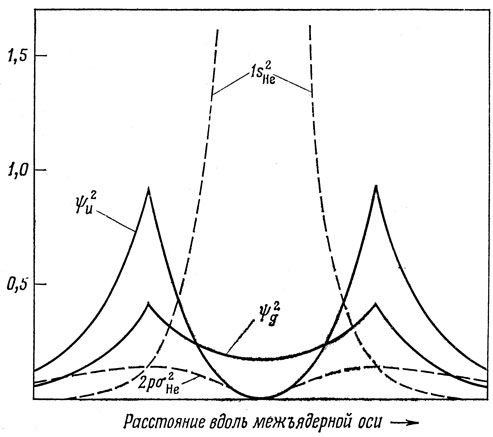
Рис. 19.7

Орбиталь ψ_g коррелирует с 1s-орбиталью Не⁺, a ψ_u с 2рσ-орбиталью Не⁺; эти орбитали имеют вид (см. табл. 3.2)

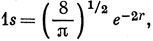
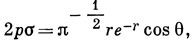
и квадраты этих орбита лей также показаны на рис. 19.7. Обратите внимание на то обстоятельство, что орбиталь ψ_u довольно хорошо передается орбиталью объединенного атома.

10.3. Ион С₂⁺ имеет электронную конфигурацию (см. табл. 10.2) КК (σ_g2s)² (σ_u2s)² (π_u2р)³. В оболочке π_u2р находятся три электрона, на один меньше максимально возможного числа. Поэтому возникают те же самые состояния, что и для конфигурации (π_u2p)¹, а именно только двукратно вырожденное состояние 2Π_u.

10.4. Представим две р-орбитали в комплексной форме π_g⁺2р, π_g^-2р [см. уравнение (11.21)]. Электрон на этих орбиталях обладает проекцией момента импульса

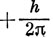
или

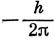
соответственно. Различные способы распределения двух электронов по этим орбиталям показаны на стр. 201. Состояние ¹Δ имеет две компоненты со следующими волновыми функциями:

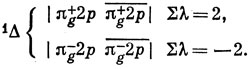
Здесь использовались для слэтеровских определителей обозначения, приведенные на стр. 115. В состоянии ³∑^- на каждой из двух орбиталей находится по одному электрону, и три спиновые функции имеют вид

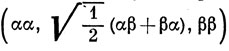
(см. стр. 167). Следовательно,

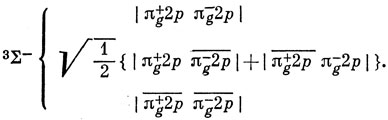
Аналогично для состояния ¹∑⁺ спиновая часть волновой функции есть

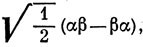
отсюда

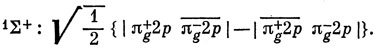
10.5. Рис. 19.8.

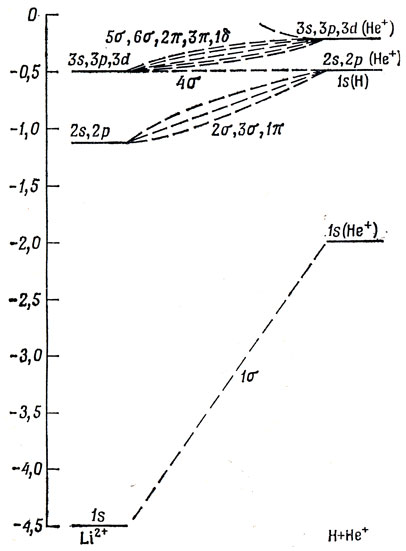
Рис. 19.8

10.6. Обозначая 1s-орбитали через 1s_a и 1s_b, нужно решить вековое уравнение [см. уравнение (6.68)]

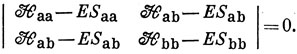
Если орбитали нормированы, S_aa = S_bb = 1. Кроме того, H_aa = H_bb. Раскрывая определитель, получим

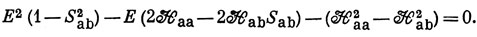
Это уравнение имеет два корня:

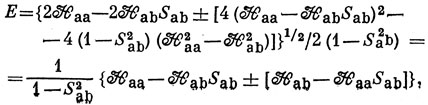
т. е.

E = (1 + S)^-1 (H_aa + H_ab) или Е = (1 - S)^-1 (H_aa - H_ab), что совпадает с выражениями (10.16).

10.7. Пусть нужно вычислить

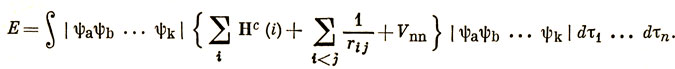
Запишем сначала определители в виде

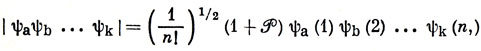
где Ρ - оператор, осуществляющий перестановку всех электронов 1 ... n по возможным спин-орбиталям и умножение на ± 1 (в зависимости от четности перестановки), чтобы обеспечить свойство антисимметрии функции.

Предположим, что используется только одно из n! слагаемых определителя, стоящего под интегралом справа; оно дает такой же вклад в энергию, как и все остальные слагаемые, поскольку все электроны эквивалентны. Умножая это слагаемое на n! (который сокращается с нормировочной постоянной), получим

После интегрирования по всем координатам, на которые не действует оператор, имеем

т. е. получается выражение (10.59).

Теперь предположим, что произведен обмен электронов на орбиталях ψ_a и ψ_b. Это дает член

Поскольку ψ_а и ψ_b - ортогональные функции, в этом интеграле не обращается в нуль только слагаемое, содержащее оператор (1/r₁₂), которое равно - K_ab. Для всех пар спин-орбиталей rs будет по одному такому члену. Если поменять местами более чем два электрона, то по крайней мере три электрона будут находиться на различных спин-орбиталях, стоящих слева и справа от оператора, и такие интегралы не вносят вклада в Е. Поэтому полная энергия равна

10.8.

Выполняя то же преобразование, что и в задаче 10.7, получим

Теперь

так как ненулевой вклад в интеграл будут вносить только операторы, содержащие координаты электрона с номером 1. Среди обменных членов от нуля отличаются лишь те, которые содержат операторы, зависящие от координат электрона 1 и любого другого электрона, например,

Суммирование таких членов по всем орбиталям (таким, как ψ_b) дает нужное выражение.