
Глава 9
9.1.
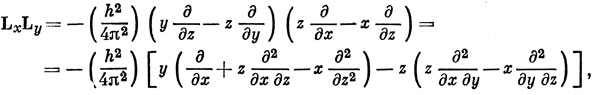
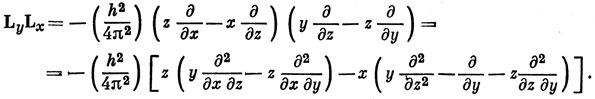
Отсюда
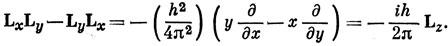
9.2.
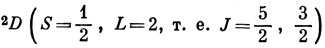
дает 2D5/2, 2D3/2,
1G (S = 0, L = 4, т. e. J = 4) дает 1G4,
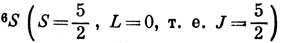
дает 6S5/2.
9.3. Для двух электронов возможны синглетное (S1 = 0) и триплетное (S1 = 1) состояния. Комбинируя эти состояния со спином третьего электрона (S2 = 1/2), имеем
S1 = 1, S2 = 1/2, S = 3/2, 1/2,
S1 = 0, S2 = 1/2, S = 1/2.
Поэтому получаем квартет и два дублета.
9.4.
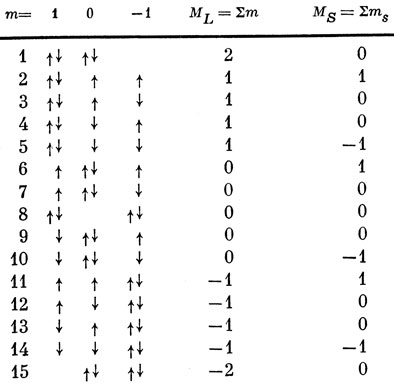
Эти состояния 1-15 имеют в точности те же значения МL и MS, что и приведенные в табл. 9.3. Следовательно, конфигурация р4 дает те же самые термы, что и конфигурация р2.
9.5.
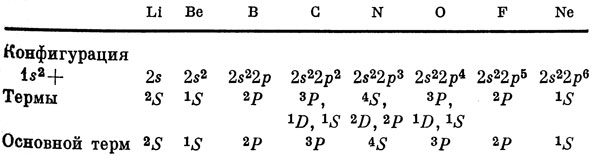
Методом, описанным для конфигурации р2, можно показать, что конфигурация р3 дает термы 4S, 2D и 2Р.
9.6. Энергия уровня с квантовыми числами J, L, S относительно средней энергии терма равна [из выражения (9.20)]
EJ = 1/2 [J (J + 1) - L (L + 1) - S (S + 1)] h2/4π2.
Энергия уровня J - 1, L, S равна
EJ-1 = 1/2 [(J - 1) J - L (L + 1) - S (S + 1)] h2/4π2.
Следовательно, EJ - EJ-1 = J h2/4π2, что доказывает правило интервалов Ланде (стр. 162).
9.7. Оболочка, заполненная менее чем наполовину, дает нормальный мультиплет (наименьшему J соответствует самая низкая энергия), но если оболочка заполнена более чем наполовину, получается обращенный мультиплет (самая низкая энергия отвечает наибольшему J). Терм 2Р дает уровни 2Р1/2 и 2P3/2. Низший уровень для конфигурации р1 есть 2Р1/2, а для конфигурации p5 - 2P3/2.
9.8. Конфигурация pd дает термы 3F, 3D, 3P, 1F, 1D, 1P. Вследствие спин-орбитального взаимодействия они расщепляются в мультиплеты 3F4, 3F3, 3F2; 3D3, 3D2, 3D1; 3P2, 3P1, 3P0; 1F3, 1D2; 1Р1. Для конфигурации 3p3d энергия межэлектронного взаимодействия много больше, чем энергия спин-орбитального взаимодействия; следовательно, уровни, имеющие одинаковые L и S, будут характеризоваться почти одинаковой энергией (энергия терма). Однако для конфигурации 3p6d спин-орбитальное взаимодействие будет больше, чем межэлектронное, и в этом случае энергия уровней зависит преимущественно от значений j обоих электронов. Электрону на р-орбитали (l = 1, s = 1/2) соответствует j = 3/2 или 1/2, а электрону на d-орбитали j = 5/2 или 3/2, Теперь получим четыре группы уровней (j1 = 3/2, j2 = 5/2; J = 4, 3, 2, 1), (j1 = 3/2, j2 = 3/2; J = 3, 2, 1, 0), (j1 = 1/2, j2 = 5/2; J = 3, 2), (j1 = 1/2, j2 = 3/2; J = 2, 1). Можно видеть, что наблюдается соответствие между значениями J, полученными из схем L - S- и j - j-связей.
9.9. Обозначим три р-орбитали символами φ1, φ0, φ-1, где индекс снизу показывает значение m. Из табл. 9.3 видно, что состояние, в котором два электрона находятся на орбитали φ1, должно быть компонентой 1D-терма. Ему соответствует антисимметризованная волновая функция, обозначаемая F2,2 (так как L = 2, ML = 2):
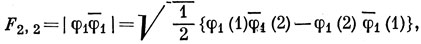
где используется обозначение, введенное на стр. 114, согласно которому спин-орбиталь со спиновой частью β отмечается чертой сверху. Действуя на F2, 2 оператором L- = Lx - iLy, получим функцию F2, 1, которая имеет L = 2, ML = 1.
Пусть L- = L- (1) + L- (2), где (1) и (2) означают два электрона. Из уравнения (9.21) видно, что
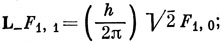
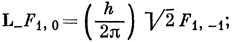
L- F1, -1 = 0.
Отсюда
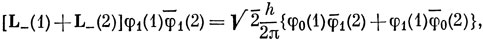
поэтому
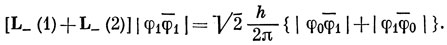
Из уравнения (9.21) снова имеем L- F2, 2 = 2 (h/2π) F2, 1, и, следовательно,
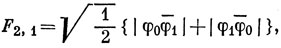
что представляет собою волновую функцию 1D-состояния с МL = 1. Действуем теперь на F2, 1 оператором L-. Имеем
[L- (1) + L- (2)] φ0 (1) φ-1 (2) = √2 h/2π {φ-1 (1) φ-1 (2) + φ0 (1) φ-0 (2)},
[L- (1) + L- (2)] φ1 (1) φ-0 (2) = √2 h/2π {φ0 (1) φ-0 (2) + φ1 (1) φ--1 (2)}.
Отсюда
[L-(1) + L- (2)] √1/2 {|φ0φ-1| + |φ1φ-0|} = h/2π {|φ-1φ-1| + |φ1φ--1| + 2 |φ0φ-0|}.
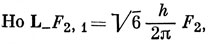
следовательно,
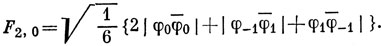
Применяя оператор L- еще два раза (или замечая, что F2, -1 и F2, -2 должны иметь такой же вид, как F2, 1 и F2, 2 с той разницей, что функции φ1 заменены на φ-1), имеем
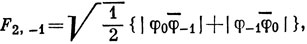
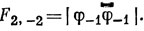
9.10. Конфигурация р2 дает термы 3Р, 1D и 1S, а конфигурация pd-термы 3F, 1F, 1D, 3D, 3Р, 1Р. Правила отбора при рассел-саундерсовой связи таковы: ΔS = 0, ΔL = 0, ±1. Следовательно, возможны следующие переходы.
3Р → 3Р, 3D; 1D → 1F, 1D, 1P; 1S → 1Р.
9.11. Терму 2Р соответствуют уровни 2Р1/2, 2P3/2 (см. задачу 9.7). Слабое магнитное поле НМ будет расщеплять терм 2P1/2 на два уровня с расстоянием между ними, равным gβHM, где [см. выражение (9.27)]
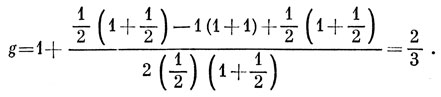
Терм 2P3/2 будет расщепляться на четыре равноотстоящих уровня с расстоянием между ними, равным gβHM, где
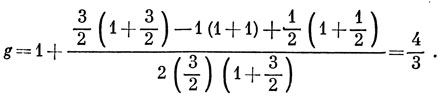
9.12. Согласно выражению (9.42), предположим
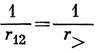
и вычислим
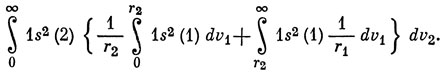
Если теперь взять 1s-орбиталь в форме 1s = 2 ζ3/2 e-ζrΥ00 (θ, φ) [см. уравнение (3.5) и табл. 3.2], где Υ00 - нормированная сферическая гармоника, то интегрирование по угловым переменным приведет выражение (а) к виду
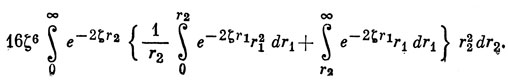
Вводя новые переменные s = 2 ζ r1, t = 2 ζ t2, имеем
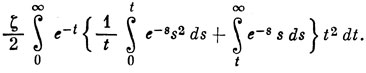
Интегрирование по частям дает
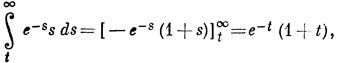
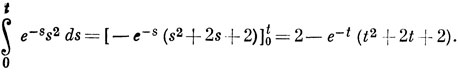
Интегрирование по t приводит к выражению
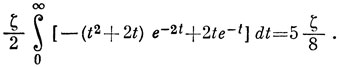
9.13. Волновая функция 3S-состояния с проекцией спина MS = 1 имеет вид
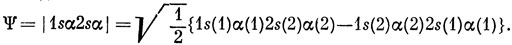
Тогда
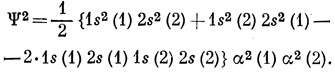
Для получения двухчастичной плотности вероятности проведем суммирование по спиновым координатам и, так как α - нормированная функция,
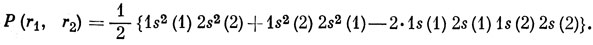
Тогда, в силу ортогональности функций 1s и 2s,
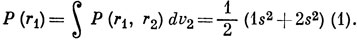
Аналогичное выражение справедливо для Р(r2). Отсюда следует, что
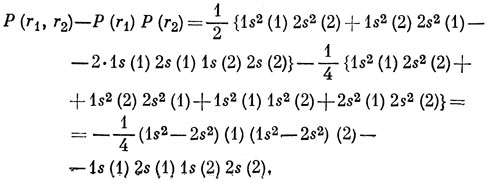
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'