Глава 8

8.1. СН₂Сl₂(С_2υ); транс-СНСl = СНСl(С_2h); C₂H₄(D_2h); IF₇(D_5h); С₆Н₅Сl(С_2υ); HCN(C_∞υ); C0₂(D_∞h).

8.2.

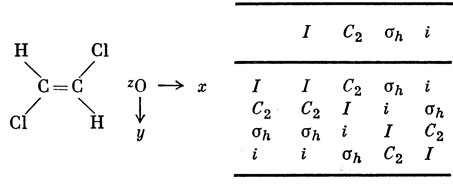
8.3.

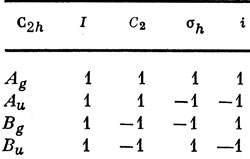
8.4. a) A₁ + A₂ + B₁ + B₂; б) 2A₂ + B₁ + 2B₂.

8.5. Для того чтобы построить представление группы, базис которого образуют АО, выясним, сколько орбиталей остаются неизменными при операциях группы (умножение на - 1 означает изменение знака).

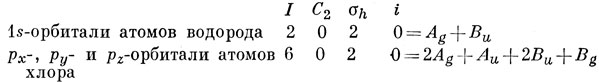
8.6.

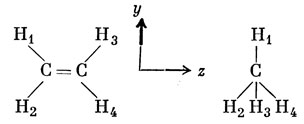
Пусть φ₁ ... φ₄ обозначают четыре водородные 1s-орбитали. Действуя так же, как и в предыдущей задаче, находим сначала, на какие НП разлагается представление, базисом которого являются эти орбитали.

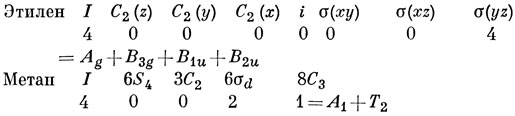
В случае этилена не возникает осложнений, вызванных наличием вырождения. Возьмем одну из функций и подвергнем ее операциям группы:

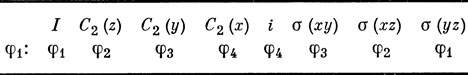
Для того чтобы построить базисы НП, умножаем функции этого набора на характеры соответствующих НП и результаты складываем:

Каждую из этих комбинаций нужно умножить на нормировочную постоянную 1/4 (в предположении, что орбитали не перекрываются друг с другом).

Подвергая функцию φ₁ операциям группы симметрии тетраэдра, получим:

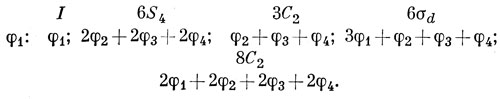
Складывая все функции этого набора, находим базис НП А₁: 6 (φ₁ + φ₂ + φ₃ + φ₄). Эту функцию надо умножить на нормировочную постоянную

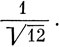
Функция, преобразующаяся по Т₂, имеет вид

Для построения двух других комбинаций, преобразующихся по НП Т₂, подвергнем операциям группы симметрии две другие орбитали:

После нормировки функции (а), (б) и (в) имеют вид

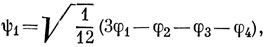
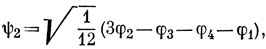
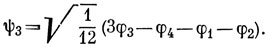
Однако эти функции не ортогональны. Выполняя с функциями ψ² и ψ₁ процедуру ортогонализации Шмидта, находим функцию

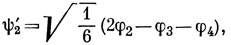
которая ортогональна к ψ₁. Наконец, ортогонализируя ψ₃ к ψ₁ и ψ₂', имеем

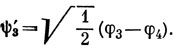
Можно, однако, получить более симметричный по виду набор функций. Например,

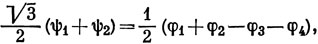
и поскольку все четыре функции эквивалентны между собой, можно переставлять местами значки 1, 2, 3 и 4 и получить еще две функции симметрии T₂:

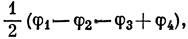
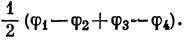
Очевидно, что эти функции взаимно ортогональны.

8.7. Таблица характеров группы дает

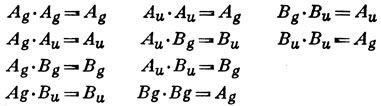
Таким образом, оператор, обладающий симметрией A_u, будет смешивать следующие состояния: A_g - А_u и B_g - В_u.