
Глава 6
6.1. Если Ψj - собственная функция оператора Β, то
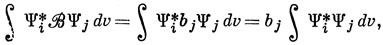
что равно нулю в силу условия ортогональности.
6.2. Если ΒΨj = bjΨj, то Β2Ψj = ΒbjΨj = bjΒΨj = bj2Ψj. Этот результат можно обобщить и показать, что bjn есть собственное значение оператора Βn.
6.3. Оператор проекции импульса есть

Он имеет собственную функцию ekx:
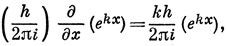
где k - действительная или комплексная постоянная. Однако если нас интересует собственная функция, которая конечна во всем интервале изменения х от -∞ до +∞, то к должно быть чисто мнимой величиной, например k = ik'. В этом случае собственная функция еik'x имеет действительное собственное значение k'h/2π.
6.4. Для одного электрона, имеющего потенциальную энергию V,
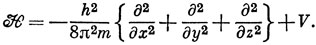
Единственным членом в H, не коммутирующим с x, является -
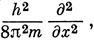
отсюда (Hx - xH) Ψ = -
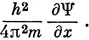
Поэтому
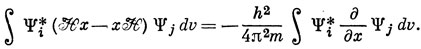
Но

и

Поэтому левая часть равенства (а) принимает вид
(Ei - Ej) ∫ Ψi* x Ψj dυ.
что приводит к искомому выражению
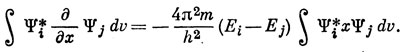
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'