Глава 17

17.1.

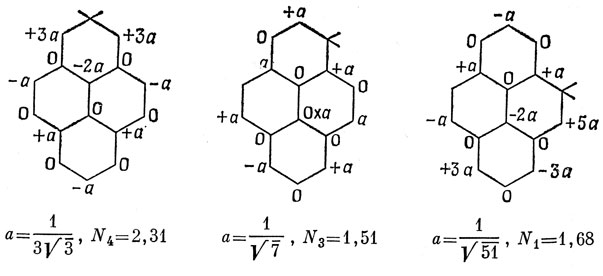
Чем меньше индекс Дьюара, тем меньше энергия локализации и легче атака. Таким образом, предсказываемые скорости атаки для пирена располагаются в следующем порядке:

17.2. Заменим отрицательно заряженный атом кислорода в нафтолятном анионе на метиленовую группу и, используя коэффициенты несвязывающих орбиталей, получим следующие заряды на атомах:

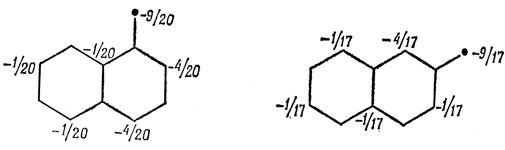
Таким образом, можно предсказать, что α-нафтол будет сочетаться с солями диазония с одинаковой легкостью в положениях 2 и 4, а β-нафтол - только в положении 1 (эти предсказания хорошо согласуются с экспериментом). Приближение изолированной молекулы дает в этом случае хорошие результаты, вероятно, потому, что нафтолятные анионы представляют собой заряженные системы, и поэтому π-электронные заряды на атомах углерода сильно различаются между собой.

17.3. Если имеются два основания B₁ и В₂ с константами K₁ и К₂ диссоциации сопряженных им кислот и нужно сравнить эти основания в данном растворителе при данной температуре, можно написать

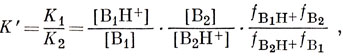
где f - коэффициент активности.

Можно, таким образом, связать константу равновесия К с изменением стандартной свободной энергии при переходе протона от B₁ к В₂:

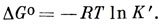
Гамметт показал, что с достаточно хорошей степенью приближения отношения коэффициентов активности для двух сходных оснований в одной и той же среде равны, т. е.

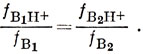
Делая такое допущение, можно приравнять ΔG° изменению потенциальной энергии при переходе протона от В₁ к В₂.

Предположим, что это изменение потенциальной энергии вызвано главным образом различием между π-электронными энергиями B₁H⁺ и В₂H⁺, т. е.

Первый вопрос, который следует поставить, таков: какой из атомов азота в аминохинолине предпочтительнее будет атакован протоном? Если это относится к гетероатому азота, то в первом приближении будем считать, что для него изменяется лишь кулоновский интеграл α; если же это относится к экзоциклической группе NH₂, то мы удаляем два электрона из π-электронной системы, поэтому протонирование атома азота в кольце приводит к меньшей потере π-электронной энергии, чем протонирование экзоциклического атома азота.

Как уже говорилось, если кулоновский интеграл μ-го атома изменяется на малую величину δα_μ, то изменение π-электронной энергии равно

δ E = q_μ δ α_μ = l,2 β q_μ.

В альтернантных углеводородах π-электронные заряды на всех атомах равны единице. Можно вычислить электронный заряд на углеродном атоме 1 в изомерных аминохинолинах, рассматривая аминогруппы, как группы CH₂^-, и помня, что можно очень просто вычислить коэффициенты в несвязывающей МО.

Значения с₀ получаются из следующих диаграмм:

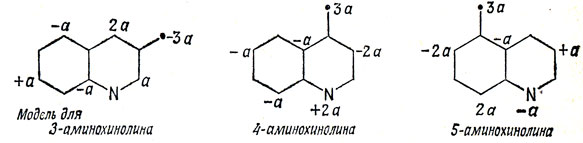
Таким образом, можно записать:

для 3-аминохинолина

pK_{3-амино-} ≈ pK_{хинолина},

для 4-аминохинолина (R = 1,98 ккал/град·моль):

для 5-аминохинолина:

Экспериментальные значения pK для 3-амино-, 4-амино- и 5-аминохинолинов равны 5; 9,2 и 5,5 соответственно.

17.4. В предыдущей задаче присоединение протона к хинолиновым основаниям не приводило к изменению общего числа π-электронов, и было вычислено изменение π-электронной энергии через изменение α. В приводимых ниже примерах при переходе от толуола к бензильному аниону или от циклопентадиена к циклопентадиенильному аниону наблюдается увеличение числа π-электронов. Предположим, что полная π-электронная энергия углеводорода АН равна 2nα + aβ, а аниона составляет (2n + 2) α + bβ (анион имеет на два π-электрона больше и еще один атом в сопряженной системе). Тогда можно выразить изменение π-электронной энергии Δε следующим образом:

где E_σ - энергия σ-связи С - Н, разрываемой в процессе ионизации, которую можно считать приблизительно одинаковой для различных σ-связей С - H. Если же рассматривать другой углеводород А'H, то различие в энергии депротонирования этих двух углеводородов дается выражением

Рассуждая так же, как и в предыдущей задаче, получим следующее выражение:

Теперь задача сводится к вычислению а, b и а', b'. Для циклопентадиена это очень просто, так как в методе Хюккеля π-электронная энергия циклопентадиена такая же, как и у бутадиена (см. стр. 353), т. е. 4,48β. π-электронная энергия циклопентадиенильного аниона получается из выражения (15.24). На орбитали ψ₁ находятся два электрона (E₁ = α + 2,00β), а на двух вырожденных орбиталях ψ₂ и ψ₃ - четыре электрона (Е₂ = Е₃ = α + 0,62β). Таким образом,

π-Электронная энергия толуола в рассматриваемых приближениях такая же, как у бензола, и из выражения (15.24) следует, что ε = 6α + 8β. Не существует простого способа определения орбитальных энергий бензильного аниона. Можно слегка упростить расчет, используя симметрию. Бензил относится к группе симметрии С₂, и можно, следовательно, нарисовать следующие диаграммы:

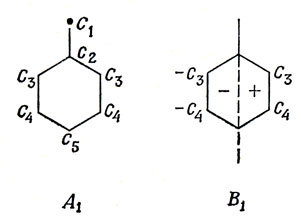
Записав, как обычно, вековые уравнения и решая их относительно х (представляют интерес только те значения х, которые отрицательны или равны нулю, так как рассматриваются только заполненные орбитали), получим следующие значения:

Поскольку бензил является нечетным альтернантным углеводородом, высшая заполненная орбиталь будет несвязывающей. Полная π-электронная энергия бензильного аниона равна 8α + 8,72β. Комбинируя эти результаты с полученными для бензола, имеем

Поэтому окончательное выражение запишется в виде

pК' - pK = 1,28·20000 / 2,303·1,987·298 ≈ 18,5.

Экспериментальное значение равно 21.