
Глава 15
15.1.
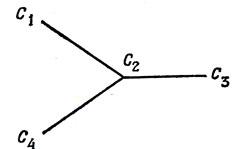
Уравнения для орбитальных коэффициентов имеют вид
xc1 + c2 = 0,
c1 + xc2 + c3 + c4 = 0,
c2 + xc3 = 0,
c2 + xc4 = 0.
Вековое уравнение
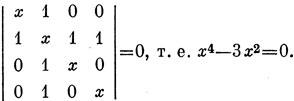
Корнями его являются x = √3 , - √3 , 0, 0, где
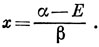
Орбитальные энергии для четырех хюккелевских орбиталей:
E1 = α + √3 β,
Е2 = α, Е3 = α, Е4 = α - √3 β.
Заметим, что состояния ψ2 и ψ3 вырождены.
Для определения коэффициентов в функции ψ1 подставим х = - √3 в уравнения для орбитальных коэффициентов:
- √3 с1 + с2 = 0, - √3 с3 + с2 = 0,
c1 - √3 с2 + с3 + с4 = 0, - √3 с4 + с2 = 0.
Отсюда
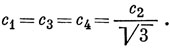
Из условия нормировки
c12 + c22 + c32 + c42 = 1
получаем
с22 + 3с12 = 1.
Окончательно
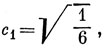
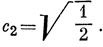
Для определения коэффициентов в функции ψ2 подставим х = 0 в уравнения и получим, что с2 = 0, c1 + c4 + c3 = 0. Любые две ортогональные между собой орбитали, удовлетворяющие этим двум условиям, дают энергии Е = α.
Такими функциями будут, например,
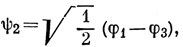
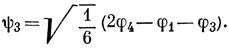
Имеются четыре электрона, которые следует разместить на трех хюккелевских орбиталях: два - на орбиталь ψ1 и, согласно правилу Гунда, по одному с параллельными спинами на вырожденные орбитали ψ2 и ψ3, так чтобы основное состояние молекулы было триплетным.
Порядок связи р12 из выражения (15.9) равен
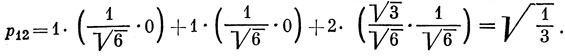
Это значение представляет интерес, так как индекс свободной валентности определен как
Fμ = nmах - nμ
[см. выражение (15.13)], где nμ - сумма π-электронных порядков связи по всем связям, исходящим из μ-го атома и nmах - максимально возможное значение этой суммы, которое имеет место как раз для рассмотренной здесь молекулы:
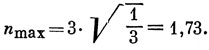
15.2. H1 - Н2 - Н3.
Вековое уравнение
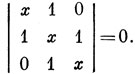
Решение его дает
x3 - 2x = 0,
х (х2 - 2) = 0,
х = - √2; 0; + √2.
Три хюккелевские орбитали следующие:
ψ1 Е1 = α + √2 β,
ψ2 Е2 = α,
ψ3 Е3 = α| - √2 β.
Полные хюккелевские энергии равны:
H3+ ε = 2 α + 2 √2 β,
H3. ε = 3 α + 2 √2 β,
Н3- ε = 4 α + 2 √2 β.
Для треугольной конфигурации Н3
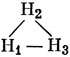
вековое уравнение
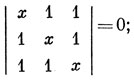
x3 - 3x + 2 = 0,
(x - 1)2 (x + 2) = 0.
Оно имеет три корня x = 1, x = 1 и x = - 2.
Как и в задаче 15.1, две орбитали вырождены. Хюккелевские энергии следующие: E1 = α + 2β, E2 = E3 = α - β, а полные хюккелевские энергии равны:
H3+ ε = 2 α + 4 β,
H3. ε = 3 α + 3 β,
Н3- ε = 4 α + 2 β.
Таким образом, согласно рассмотренному приближению, H3+ имеет более низкую энергию в треугольной конфигурации; для H3. обе конфигурации обладают почти одинаковой энергией; для треугольной конфигурации Н3 энергия лишь немного ниже, чем для линейной; для Н3- линейная конфигурация имеет заметно более низкую энергию, чем треугольная. Полученный здесь результат для Н3. не согласуется с результатами более точных расчетов, согласно которым линейная конфигурация более стабильна.
15.3. Молекула фульвена принадлежит к группе симметрии С2υ: орбитали будут симметричны или антисимметричны относительно поворота вокруг оси С2, и если эти орбитали являются π-орбиталями, то они антисимметричны относительно отражения в плоскости молекулы.
Возможные типы симметрии:
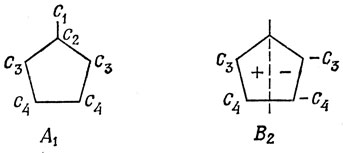
Используя метод, описанный на стр. 357-362, можно на основе этих диаграмм сразу написать уравнения для коэффициентов:
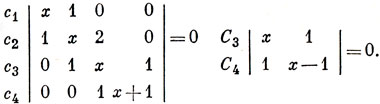
Вековые уравнения: х4 + х3 - 4x2 - 3x + 1 = 0, x2 - х - 1 = 0.
Корни этих уравнений таковы:
х = - 2,115; - 1; - 0,618; + 0,254; + 1,618; + 1,861.
Ниже приведена полная таблица орбитальных коэффициентов для связывающих орбиталей:

Это дает
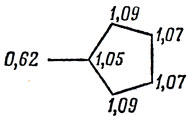
Вычитая значение qν из заряда + 1 остова каждого атома, получаем следующие значения эффективных зарядов:
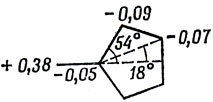
Для вычисления дипольного момента поместим начало координат в атом углерода с номером 2 и будем считать длины всех связей равными 1,40 А (средняя длина простой и двойной связи):
μ = ∑ν qν rν = 1,40 · 10-8 [0,38 + 2 (0,09) cos 54° + 2 (0,07) 2 (cos 54°) cos 18°] · 4,8 · 10-10 CGSE = 4,3 · 10-18 CGSE = 4,3 D.
Момент направлен вдоль оси С2.
Экспериментальное значение дипольного момента составляет лишь 1,2 D, что подчеркивает ограниченность метода Хюккеля в применении к неальтернантным углеводородам (см. стр. 383).
15.4. Если через Н' обозначить возмущение одноэлектронного гамильтониана, обусловленное введением заместителя, то возмущенные орбитали определятся выражением
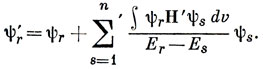
Штрих у знака суммы означает, что отсутствует член с r = s. Поскольку
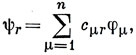
где φμ - атомные орбитали,
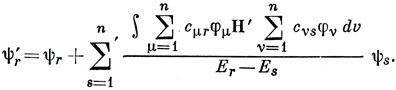
Если возмущение Н' изменяет только кулоновский интеграл μ-го атома, то, учитывая, что
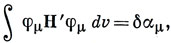
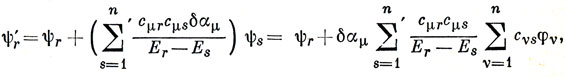
можно записать ψr' в виде
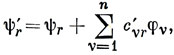
где
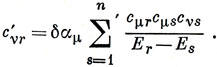
Изменение π-электронного заряда на ν-м атоме равно
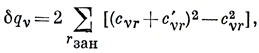
где суммирование проводится по занятым орбиталям.
δ qν = 4 ∑r зан cνr cνr' малые члены, содержащие (cνr')2. Подставляя cνr', имеем
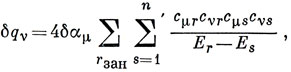
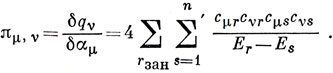
В сумме по s можно отделить суммирование по занятым и незанятым орбиталям:
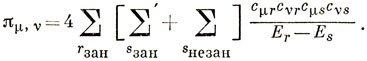
Двойная сумма по занятым орбиталям даст нуль, так как для каждого члена
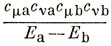
найдется член
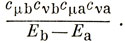
Отсюда следует, что
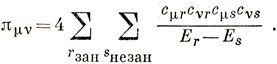
15.5. На следующей диаграмме изображен правильный многоугольник, вписанный в круг радиуса 2|β|:
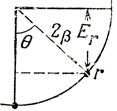
Энергия, соответствующая вершине r, указанной на диаграмме, равна Er = 2 β cos θ.
Для многоугольника с t сторонами θ = 2πr/t, где r = 0 ... t/2 (t - четное) или r = 0 ... t-1/2 (t - нечетное), Er = 2 β cos 2πr/t.
15.6. Если не учитывать взаимодействия между различными двойными связями, то орбитали получатся те же, что и для трех молекул этилена: три связывающие и три разрыхляющие. Молекула имеет горизонтальную плоскость симметрии; три связывающие орбитали симметричны относительно отражения в этой плоскости, а три разрыхляющие орбитали - антисимметричны. Отсюда следует, что если включать члены с β', учитывающие взаимодействие между орбиталями различных двойных связей, то связывающие орбитали могут взаимодействовать только со связывающими, а разрыхляющие - с разрыхляющими; взаимодействия же связывающих орбита лей с разрыхляющими не будет, так как они имеют различную симметрию. Хотя взаимодействие между связывающими орбиталями и будет изменять их энергию, полная энергия трех связывающих орбиталей останется неизменной, и поэтому такое взаимодействие не приведет к дополнительному понижению энергии системы.
15.7. Взаимные поляризуемости атомов в молекуле бутадиена можно было бы вычислить непосредственно из выражения (15.36), но на практике легче упростить это выражение, пользуясь свойствами альтернантных углеводородов с четным числом атомов углеводорода, к которым относится бутадиен:
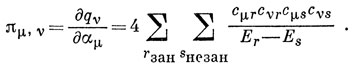
Как уже говорилось, когда число атомов углерода n - четное, молекулярные орбитали можно разбить на пары с равными по величине и противоположными по знаку энергиями для орбиталей каждой пары. Пронумеруем хюккелевские орбитальные энергии в порядке возрастания от E1 до Еn:
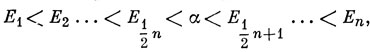
тогда
En-r+1 = - Еr.
π-Электроны в количестве n занимают нижние n/2 МО. Поэтому выражение (15.36) упрощается и записывается в виде
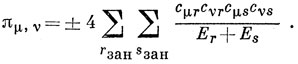
Знак плюс нужно взять, если μ-й и ν-й атомы относятся к одному набору (помеченному или непомеченному), знак минус - когда они относятся к разным наборам.
Следовательно, для углеродных атомов 1 и 2 в молекуле бутадиена имеем
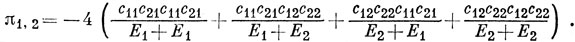
Используя значения энергий и коэффициентов, приведенные на стр. 351, получим

Выполняя расчет для других замещений, получим следующую таблицу:
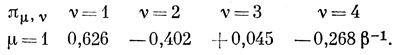
π-Электронные заряды qμ равны
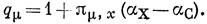
При расчете молекулы акролеина заменяем углеродный атом 1, 1 кислородом, следовательно, αO = αС + hO β.
Пусть hO = 1, тогда αO = αС = β и заряды qμ равны

15.8. МО этилена определяются симметрией молекулы:
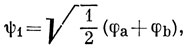
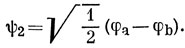
В основном состоянии два электрона с противоположными спинами находятся на связывающей орбитали:
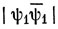
Этой функции соответствует энергия [см. выражение (10.79)]
Е = 2 H11c + J11 + Vnn.
Выражая МО через АО, получим
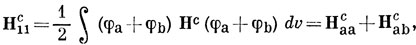
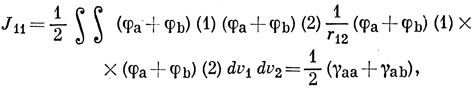
где γ определено по уравнению (15.44).
Обозначим Habc через β и из выражения (15.52) имеем
Haac = I - γab.
Следовательно,
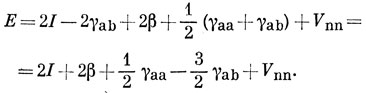
15.9. Согласно выражению (15.59), энергия r-й орбитали равна
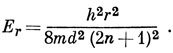
Полиен с 2n атомами углерода имеет 2n электронов, и они заполняют n низших МО. Высшей занятой орбитали соответствует энергия
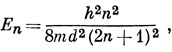
а низшей вакантной -
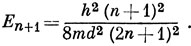
Разность этих энергий
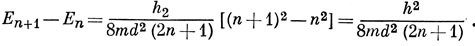
Эту величину можно приравнять энергии, необходимой для перехода молекулы в первое возбужденное состояние; тогда длина волны в максимуме соответствующей полосы поглощения равна
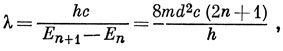
откуда видно, что λ ∼ n.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'