Мул: лошадь ↔ осел

Казалось бы все ясно: формула Кекуле неверна, надо ее забыть, заменить другой, более точно передающей истинное положение вещей, например, шестиугольником со вписанной в него окружностью (эта, окружность символизирует шестерку π-электронов, усредненных между всеми атомами углерода).

Но химики не спешат расставаться с формулой Кекуле: она удобна и привычна и для многих целей вполне удовлетворительна. Главное только - помнить, что скрывается за этой формулой.

В 30-е годы американский ученый Лайнус Полинг нашел новое применение привычной, но неточной формуле. Формула Кекуле была использована в квантовохимических расчетах молекулы бензола.

Известно, что электрон обладает одновременно свойствами частицы и волны. Поведение электрона в квантовой механике описывается так называемой волновой функцией φ (пси). Для того чтобы определить вид этой функции, необходимо решить уравнение Шредингера, которое показывает зависимость изменения φ от силового поля, в котором движется электрон. Это уравнение имеет достаточно сложный вид:

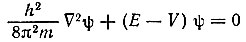
где Е - полная энергия электрона, V - его потенциальная энергия, m - масса электрона, h - постоянная Планка.

В этом уравнении ∇² - это оператор, который означает дифференцирование функции φ, т. е.

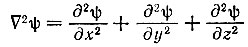
Сложно? Еще сложнее решение этого уравнения. Но пусть не пугается читатель, не знакомый с высшей математикой - мы не будем решать уравнения Шредингера. В большинстве случаев (мы имеем в виду многоэлектронные молекулы) эта задача непосильна даже для электронно-вычислительных машин. Но ученые находят приближенные методы, которые позволяют все-таки на основе расчета узнать многое о поведении электронов в молекуле. Один из таких методов и предложил Полинг.

Полинг представляет бензол в виде двух формул Кекуле (А и В):

Волновая функция φ для реально существующей молекулы бензола приближенно равна сумме волновых функций φ_A и φ_В не существующих в действительности структур А и В:

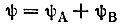
Волновую функцию φ называют резонансной.

При всех таких формальных математических манипуляциях главное - не забывать, что отдельные резонансные структуры А и В не выражают реальных состояний молекулы бензола. Основоположники описываемой нами теории резонанса проводили такое сравнение.

Мул -это гибрид лошади с ослом. И поэтому, если мы хотим человеку, никогда не видевшему мула, описать это животное, мы можем рассказать о лошади, об осле, а потом заявить: мул - это нечто среднее. Такое сравнение страдает одним недостатком - и осел, и лошадь, и мул существуют в действительности, а циклогексатриен, изображаемый формулой Кекуле, не встречается в природе.

В теории резонанса бензол изображается двумя структурами Кекуле с "обоюдной" стрелкой между ними:

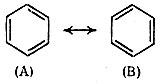
Здесь следует вспомнить, что еще Кекуле понимал недостатки своей формулы и ввел представление о постоянном перемещении двойных связей, В результате такого перемещения структура А, по Кекуле, быстро и обратимо переходит в структуру В. Кекуле, как мы знаем, обозначал это двумя стрелками (см. с. 26).

Есть ли разница между стрелками Кекуле и стрелкой в теории резонанса? Есть, и разница принципиальная.

У Кекуле стрелки обозначают процесс, идущий во времени. Предположим, что мы имеем фотоаппарат, позволяющий фотографировать молекулу бензола с любой, сколь угодно короткой выдержкой* Сфотографируем скопление молекул бензола с выдержкой меньшей, чем то время, которое требуется для перехода структуры А в структуру В и наоборот. Что мы увидим на фотоснимке? Что половина всех молекул бензола присутствует в виде структуры А, другая половина - в виде структуры В. Но достаточно повернуть структуру А на 60° в плоскости чертежа, и она совпадет со структурой В. Значит, на предполагаемом снимке мы увидим все молекулы в виде структуры по Кекуле: в шестиугольниках должны будут чередоваться связи разной длины-o двойные и простые.

Но мы знаем, что современные физические методы установили отсутствие перемещений двойных связей по молекуле. Значит, изображать молекулу бензола по Кекуле - в виде двух структур с двумя стрелками между ними - в корне неверно.

Теперь обратимся к обоюдоострой стрелке.

Вспомним древнюю мифологию. Кентавр - гибрид человека и лошади, сфинкс - гибрид человека и льва. В этих случаях мы, желая описать кентавра и сфинкса, можем сделать это таким образом:

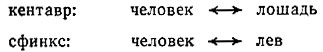
Итак, мы теперь имеем примеры всех трех типов описания гибридов: 1) и гибрид, и его родители существуют (мул); 2) родители реально существуют, гибрид - плод воображения (кентавр, сфинкс); 3) гибрид реально существует, а родители - плод воображения, абстракции (бензол и формулы Кекуле).