
Внутренние взаимодействия в кристаллах с редкоземельными ионами (У.Х. Копвиллем)
Спин-система ионов рзэ в кристаллах многократно изучалась путем измерения магнитной восприимчивости и теплоемкости [1, 2], а также методами парамагнитного резонанса [3]. Даже при гелиевых температурах магнитный момент ионов рзэ содержит вклад от орбитального движения электронов, что обусловливает сильную анизотропию параметров спин-системы. Поэтому кристаллы с редкоземельными ионами являются ценным рабочим веществом при создании установок для поляризации ядер, получения сверхнизких температур, генерации и усиления гиперзвука, радиоволн и света.
В настоящей работе исследуется природа внутренних взаимодействий спин-системы этилсульфата церия.
В отличие от этилсульфата неодима, где H1 при гелиевых температурах описывается оператором магнитных диполь-дипольных взаимодействий Hg, спин-система Ce(C2H5SO4) × 9Н2O содержит еще вклад спин-спиновых взаимодействий иной природы. В дальнейшем мы примем, что Н1 = Hg + Hс + Ноб, где Hс и Hoб - операторы электрических квадруполь-квадрупольных и обменных взаимодействий. Далее мы вычислим приведенный второй момент 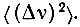 в частотных единицах от линии ЭПР основного дублета, расщепленного статическим магнитным полем Н0. Сравнение теоретических и экспериментальных значений
в частотных единицах от линии ЭПР основного дублета, расщепленного статическим магнитным полем Н0. Сравнение теоретических и экспериментальных значений 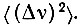 позволит установить вид H1 и оценить порядок величин Hg, Нс и Hоб.
позволит установить вид H1 и оценить порядок величин Hg, Нс и Hоб.
Состояние 2F5/2 иона Се3+ в кристаллическом поле расщепляется на три дублета - 1 ± 5/2 , 1 ± 1/2, 1 ± 3/2, соответствующие энергии 0; δ1 = 4,7 ± 0,1 см-1; δ2 = 100-150 см-1 [4]. Для описания формы линии ЭПГ при эффективном спине S' = 1/2 кроме оператора Hg можно ввести оператор [5]:
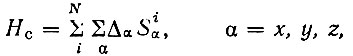 (1)
(1)где α - главные оси тензора Δ; N - число магнитных частиц.
Если сильное статическое магнитное поле Hоα параллельно оси α, а переменное магнитное поле Ht ⊥ α, то приведенный второй момент кривой парамагнитного резонанса имеет такой вид:
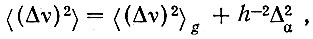 (2)
(2)
где вклад 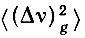 от Нg вычисляется по формулам (23 и 24) работы [6]. Сравнение равенства (2) с экспериментом [3] определяет значение Δz ∼ 0,003 см-1 для Ce(C2H5SO4)3 × 9Н2O, ЧТО совпадает со значением Q1 = Δz, измеренным статическим методом [2, 4].
от Нg вычисляется по формулам (23 и 24) работы [6]. Сравнение равенства (2) с экспериментом [3] определяет значение Δz ∼ 0,003 см-1 для Ce(C2H5SO4)3 × 9Н2O, ЧТО совпадает со значением Q1 = Δz, измеренным статическим методом [2, 4].
Основной интерес представляет физическая природа величины Δz. Если считать, что Δz характеризует неразрешенную тонкую структуру ЭПР, обусловленную электрическим квадруполь-квадрупольными взаимодействиями между ионами Се3+ [4], то
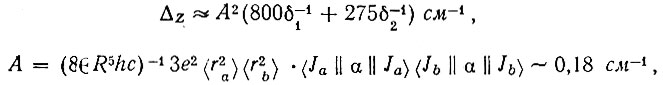 (3)
(3)
где R - расстояние между ближайшими соседними ионами а и b вдоль тригональной оси кристалла; 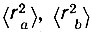 - соответствующие средние квадраты радиусов траекторий 4f-электрoнoв;
- соответствующие средние квадраты радиусов траекторий 4f-электрoнoв; 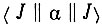 - переходные коэффициенты [7]; g - диэлектрическая постоянная, учитывающая экранировку электрического потенциала другими молекулами (в данном случае - молекулами воды).
- переходные коэффициенты [7]; g - диэлектрическая постоянная, учитывающая экранировку электрического потенциала другими молекулами (в данном случае - молекулами воды).
Было показано [4], что полученное на основании формулы (3) значение 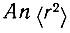 противоречит некоторым экспериментальным данным по измерению теплоемкости при низких температурах и теории кристаллического поля. Поэтому представляет интерес исследование влияния обменных взаимодействий Нoб между магнитными ионами на
противоречит некоторым экспериментальным данным по измерению теплоемкости при низких температурах и теории кристаллического поля. Поэтому представляет интерес исследование влияния обменных взаимодействий Нoб между магнитными ионами на 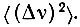 .
.
С учетом Hоб формула (2) примет такой вид [5]:
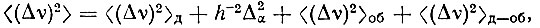 (4)
(4)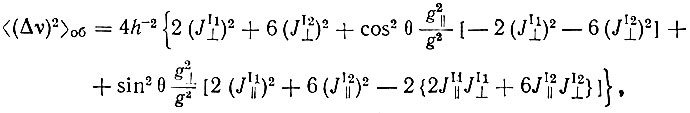 (5)
(5)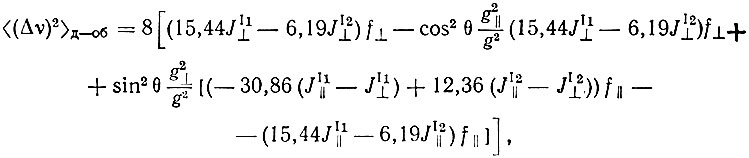 (6)
(6)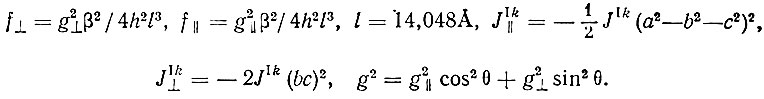
Формулы (5 и 6) относятся к основному дублету иона Се3+
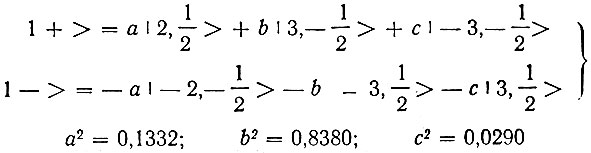
и учитывают взаимодействие центрального иона l с ионом k, расположенными в первой (k = 1) и во второй (k = 2) координационных сферах. Волновые функции ( L, m> характеризуются орбитальным L и спиновым m квантовыми числами [7]; θ - угол между направлением поля Hα и тригональной осью кристалла; β - магнетон Бора; g⊥ и g|| - факторы спектроскопического расщепления; JIk - обычный обменный интеграл [8]; l - длина элементарной ячейки магнитной решетки.
Из формулы (5) и (6) следует, что вклад обменных взаимодействий зависит от угла θ; при θ = 0 вклад <(Δν)2>об = 0.
Формулы (2) и (5), (6) в разной степени зависят от направления поля Н относительно осей кристалла, что может быть использовано для выделения вкладов в 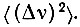 от Hс и Ноб. Отметим, что в случае переходов между различными дублетами вид формул (2) и (5, 6) изменится, причем вклад от Hс возрастет во много раз.
от Hс и Ноб. Отметим, что в случае переходов между различными дублетами вид формул (2) и (5, 6) изменится, причем вклад от Hс возрастет во много раз.
Литература
- А. Н. Cooke, S. Whitley, W. P. Wolf. Proc. Phys. Soc., B68, 415 (1955).
- С. E. Johnson, H. Meyer. Proc. Roy. Soc., A253, 199 (1959).
- A. Bogle, A. H. Cooke, S. Whitley. Proc. Phys. Soc. A64, 931 (1951).
- B. Bleaney. Proc. Phys. Soc., 77, 113, (1961).
- У. X. Копвиллем. Диссертация. Казань, 1958.
- У. X. Копвиллем. Физика металлов и металловедение, 8, 8 (1959).
- R. J. Elliott, К. W. Stevens. Proc. Roy. Soc., A215, 437 (1952); A218, 553 (1953).
- J. H. Van Vleck. Phys. Rev., 74, 1168 (1948).
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'