5. Теория электростатического кристаллического поля

Метод валентных связей и теория электростатического кристаллического поля существенно различаются. Первая исходит из предположения, что координационная связь ковалентна. Электростатическая теория полностью отвергает ковалентный характер связи и предполагает, что связь между ионом металла и лигандом целиком ионная. Вычисления энергии координационной связи можно сделать, используя классические уравнения потенциальной энергии, учитывающие силы притяжения и отталкивания между заряженными частицами (15).

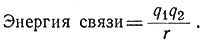
(15)

В уравнении (15) q₁ и q₂ - заряды взаимодействующих ионов, r - расстояние между центрами ионов. Аналогичное уравнение применяют и для описания взаимодействия незаряженной полярной молекулы с ионом. Это приближение дает результаты, достаточно хорошо совпадающие с экспериментально найденными значениями энергии связи для комплексов непереходных металлов. Для комплексов переходных металлов вычисленные значения оказываются часто слишком малыми. Это несоответствие в значительной степени исправляется, если рассматривать орбиты d-электронов и сделать допущение о влиянии лигандов на относительные энергии d-орбит.

Такое усовершенствование электростатической теории было впервые разработано и использовано физиками Бете и Ван Флеком в 1930 г. для объяснения цвета и магнитных свойств кристаллических солей. Их теория известна как теория кристаллического поля (ТКП). Несмотря на то что эта теория была предложена в то же время или даже немного раньше, чем метод валентных связей, потребовалось около двадцати лет, чтобы ТКП стала известна химикам и ими использована. Возможно, причиной было то, что ТКП была написана для физиков, а МВС давал химикам удовлетворительное наглядное представление о связи между атомами.

В 1951 г. несколько химиков-теоретиков независимо друг от друга применили ТКП для объяснения спектров комплексов переходных металлов. Так как этот метод оказался удачным, то немедленно последовала целая серия исследований. Скоро выяснилось, что ТКП пригодна для полуколичественного объяснения многих известных свойств координационных соединений.

Чтобы понять ТКП, необходимо мысленно ясно представлять пространственную ориентацию d-орбит (рис. 6). Взаимодействие d-орбит переходных металлов с лигандами, окружающими металл, порождает эффект кристаллического поля. Для иллюстрации ТКП можно рассмотреть октаэдрический комплекс [TiF₆]^2-. В свободном ионе Ti⁴⁺, изолированном в пространстве, электронная конфигурация следующая: 1s²2s²2p⁶3s²3p⁶; d-электронов у него нет. Пять пустых 3d-орбит в этом ионе характеризуются одинаковой энергией. Это позволяет предположить, что электрон может находиться на одной из этих d-орбит с равной вероятностью. Орбиты, соответствующие одному и тому же значению энергии, называются вырожденными орбитами.

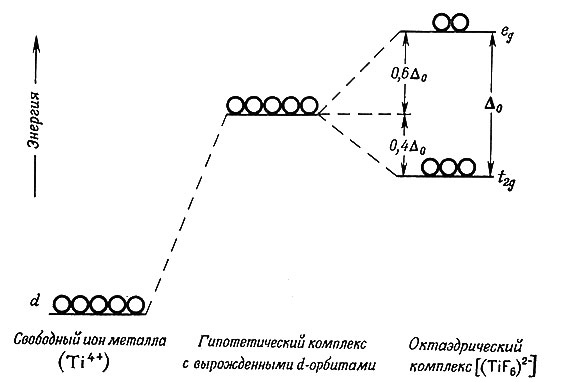
Рис. 8. Схематическая диаграмма уровней энергии d-орбит свободного иона металла, гипотетического комплекса, в котором нет расщепления кристаллическим полем, и октаэдрического комплекса

В [TiF₆]^2- ион Ti⁴⁺ окружен шестью ионами F^-. Наличие этих ионов F^-, отталкивающее действие их отрицательных зарядов затрудняют заполнение электронами d-орбит в ионе Ti⁴⁺. Другими словами, ионы F^- (или другие лиганды) при приближении к d-орбитам увеличивают соответствующую им энергию (рис. 8). Если бы шесть ионов F^-, окружающих ион Ti⁴⁺ в [TiF₆]^2-, располагались бы на одинаковом расстоянии от пяти d-орбит Ti⁴⁺, то всем этим d-орбитам соответствовало бы одно и то же значение энергии (они были бы вырожденными), но значительно большее, чем то, которое свойственно свободному иону Ti⁴⁺. Однако октаэдрический комплекс со всеми вырожденными d-орбитами является гипотетическим.

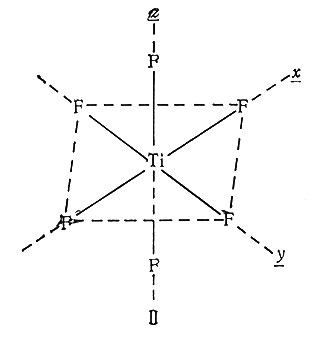
Комплекс [TiF₆]^2- имеет октаэдрическую структуру; для удобства будем рассматривать этот комплекс, считая, что шесть ионов F^- будут располагаться на осях x, y, z декартовой системы координат (II). При таком расположении ионы ближе всего будут находиться от d_x²-y²- и d_z²-орбит, которые называют e_g-орбитами (рис. 6). Действительно, e_g-орбиты направлены прямо на лиганды F^-, в то время как d_xy-, d_xz- и d_yz-орбиты, обозначаемые t_2g-орбитами, направлены между лигандами^*. Поэтому электронам труднее занять место на e_g-орбите, чем на t_2g-орбите, откуда следует, что e_g-орбиты характеризуются более высоким значением энергии, чем t_2g. Такое разделение пяти вырожденных орбит свободного иона металла на группы d-орбит, характеризующихся разной энергией, является главной особенностью ТКП. Это явление назвали расщеплением кристаллическим полем. Как следует из сказанного, расщепление уровней энергии происходит оттого, что d-орбиты имеют неодинаковую ориентацию в пространстве, и соседние атомы, ионы или молекулы могут изменять энергию направленных к ним орбит.

^* (Обозначения e_g и t_2g используют в математической теории групп, t указывает на трехкратное вырождение, e - на двукратное.)

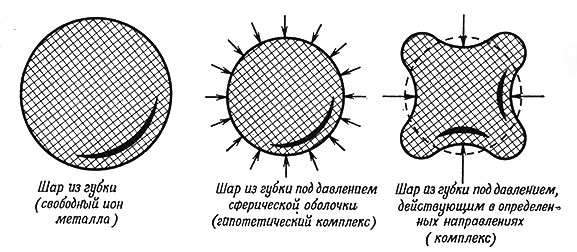
Рис. 9. Эффект кристаллического поля наглядно представлен как давление сферической оболочки на шар из губки и как давление на тот же шар, сконцентрированное в определенных местах. Сравните с рис. 8

Многие студенты считают, что ТКП и ее концепция расщепления кристаллическим полем трудна для наглядного представления. Выше была сделана попытка описать самые существенные положения на основании пространственных моделей d-орбит. Это правильный подход к ТКП. Однако полезно также показать простую физическую картину расщепления кристаллическим полем. Обратимся к рис. 9 и предположим, что ион металла с его электронным облаком может быть представлен в виде упругого шара из губки. Теперь посмотрим, что с ним станет, если снаружи на него будет действовать жесткая сферическая оболочка (соответствующая лигандам). Объем шара уменьшится, и система будет иметь более высокую энергию, что подтверждается тем фактом, что упругий шар самопроизвольно расширится и примет первоначальный объем после удаления стягивающей его оболочки. Это изменение энергии соответствует увеличению энергии, которое возникает в результате отталкивания между электронами в ионе металла и электронами лигандов в гипотетическом комплексе (рис. 8).

Если теперь жесткая оболочка сконцентрирует общую действующую силу в шести отдельных точках (например, в углах октаэдра), то шар вдавится внутрь в этих точках и будет выпячиваться между ними. В результате такого сжатия системы губка в шести точках повышенного давления будет иметь более высокую энергию, а между этими точками - более низкую. Это соответствует расщеплению кристаллическим полем, причем выпяченные места соответствуют t_2g-орбитам, а вдавленные точки - e_g-орбитам.

Ранее было отмечено, что энергия, соответствующая d-орбитам иона металла, возрастает, если лиганды приближаются к иону. Это само по себе уже позволяет предположить, что комплекс должен быть менее устойчивым, чем свободный ион металла и свободные лиганды. Однако сам факт образования комплекса указывает на то, что комплекс является конфигурацией, имеющей меньшую энергию, чем порознь ион металла и лиганды. Увеличение энергии d-орбит иона металла вполне компенсируется за счет энергии образования связи между ионом металла и лигандом.

В октаэдрическом поле лигандов t_2g- и e_g-орбитам иона соответствуют различные энергии. Разность величин энергии обозначается через Δ₀. Можно доказать при помощи геометрии октаэдрических систем, что энергия, соответствующая t_2g-орбитам, на 0,4Δ₀ меньше энергии пятикратно вырожденных d-орбит гипотетического комплекса, т. е. того комплекса, который получился бы, если бы не происходило расщепления кристаллическим полем (рис. 8). По этой же причине и e_g-орбитам соответствует энергия на 0,6Δ₀ выше, чем пятикратно вырожденной гипотетической орбите.

В октаэдрическом комплексе, в котором имеется один d-электрон (например, [Ti(H₂O)₆]³⁺), этот d-электрон находится на d-орбите с наинизшей энергией. При помощи простой электростатической теории нельзя установить, что d-орбитам в комплексе соответствуют различные значения энергии. Поэтому эта теория предполагает, что d-электрон должен иметь энергию гипотетической вырожденной d-орбиты. В действительности же d-электрон попадает на t_2g-орбиту с энергией на 0,4Δ₀ меньше энергии гипотетической вырожденной орбиты, и потому комплекс будет на 0,4Δ₀ более стабилен, чем следует на основании простой электростатической модели. Можно просто сказать, что d-электрон, а следовательно, и весь комплекс имеет меньшую энергию вследствие нахождения электрона на (t_2g) d-орбите, которая возможно более удалена от лиганда. Для комплекса величина 0,4Δ₀ называется энергией стабилизации кристаллическим полем (ЭСКП). В табл. 7 приведены энергии стабилизации кристаллическим полем для ионов металов в октаэдрических комплексах. Отметим, что величины стабилизации кристаллическим полем легко вычислить путем прибавления величины 0,4Δ₀ каждому электрону, занимающему t_2g-орбиту, и величины -0,6Δ₀ каждому электрону, занимающему e_g-орбиту. Таким образом, ЭСКП для системы с пятью d-электронами равна либо 3(0,4Δ₀) + 2(-0,6Δ₀) = 0,0Δ₀, либо 5 (0,4Δ₀) + 0 (-0,6Δ₀) = 2,0Δ₀, т. е. зависит от распределения пяти электронов по t_2g- и e_g-орбитам.

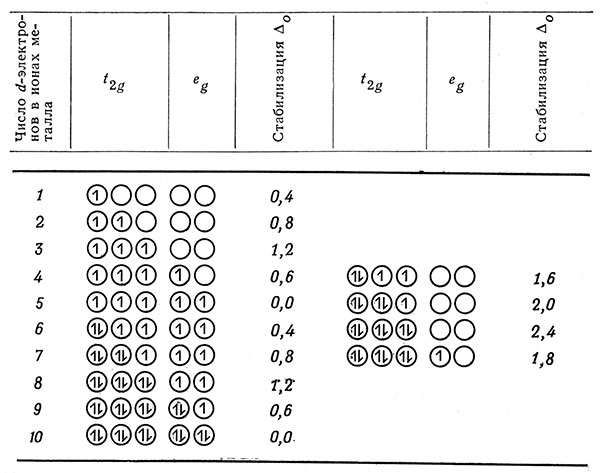
Таблица 7. Энергии стабилизации кристаллическим полем для ионов металлов в октаэдрических комплексах

Простая электростатическая теория рассматривает ион металла как атомное ядро, окруженное сферическим электронным облаком. Теория кристаллического поля предполагает лучшую модель, так как она допускает, что d-электроны образуют несферическое электронное облако вследствие их стремления избежать те места, в которых находятся лиганды. (Они образуют несферические электронные облака путем избирательного заполнения орбит с низкими значениями энергии, направленных между лигандами). Поэтому теория кристаллического поля объясняет по вполне понятным соображениям, почему при посредстве простых электростатических вычислений получают более низкие значения устойчивости комплексов и соединений переходных металлов; простая теория пренебрегает несферичностью распределения электронов и возникающей вследствие этого энергией стабилизации кристаллическим полем.

Одним из ранних возражений против применения простой электростатической теории связи для комплексов металлов была невозможность объяснения с позиций этой теории образования плоских квадратных комплексов. Доказано, что если четыре отрицательных заряда удерживаются вокруг положительного центрального иона только одними электростатическими силами, то отрицательные заряды должны находиться в вершинах тетраэдра. Только при таком расположении отрицательные группы находятся на максимальном расстоянии друг то друга и испытывают наименьшее электростатическое отталкивание. Это отвечает действительности при условии, если центральный ион имеет сферическую симметрию. Однако такая симметрия не типична для ионов переходных металлов, так как электроны находятся на орбитах с низкой энергией, которые направлены между лигандами и не имеют сферической симметрии. В дальнейшем в разд. 1 гл. III будет показано, что ТКП позволяет объяснить существование плоских квадратных комплексов, а также предсказать неустойчивость некоторых октаэдрических комплексов.

Итак, был рассмотрен случай расщепления кристаллическим полем для октаэдрических комплексов, теперь следует остановиться на комплексах другого геометрического строения. Удобно начинать рассмотрение расщепления кристаллическим полем с октаэдрической структуры и проследить затем, как оно изменяется с изменением геометрической конфигурации (рис. 10). При переходе от правильного октаэдра к плоским квадратным структурам изменение сводится к удалению из октаэдра каких-либо двух лигандов, находящихся в транс-положении. Обычно, говоря о квадрате, имеется в виду плоскость xy и подразумевается удаление из октаэдра транс-лигандов, расположенных по оси z.

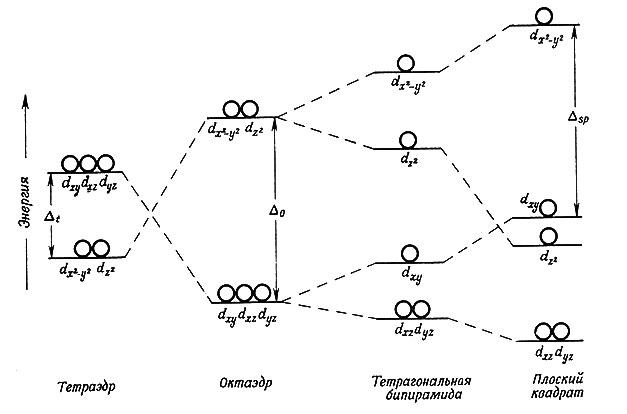
Рис. 10. Схема расщепления кристаллическим полем d-орбит центрального иона в комплексах различных симметрии. Индексы при Δ относятся к симметрии

Если лиганды на оси z будут смещены так, что расстояние металл - лиганд станет немного больше, чем расстояния для четырех лигандов в плоскости xy, то в результате получится тетрагональная структура (рис. 10). Это позволит лигандам в плоскости xy приблизиться к центральному иону. Соответственно d-орбиты в плоскости xy будут испытывать большее отталкивание от лигандов, чем это имело место в октаэдрической структуре, что выразится в увеличении энергии d_x²-y²- и d_xy-орбит (рис. 10). В то же время d-орбиты, ориентированные по оси z или в плоскостях xz и yz, будут испытывать меньшее отталкивание от лигандов, которые теперь удалены по оси z на некоторое расстояние. Это приведет к значительному уменьшению энергии d_z²-орбиты и небольшому уменьшению энергии d_xz- и d_yz-орбит по сравнению с октаэдрической конфигурацией.

Аналогичная картина расщепления будет наблюдаться и для квадратной пирамидальной структуры, в которой один лиганд находится на оси z, а четыре остальных лиганда и центральный ион располагаются в плоскости xy. Полное удаление двух лигандов по оси z, приводящее к образованию плоских квадратных конфигураций, сопровождается дальнейшим увеличением энергии d_x²-y²- и d_xy-орбит и уменьшением энергии d_z²-, d_xz- и d_yz-орбит.

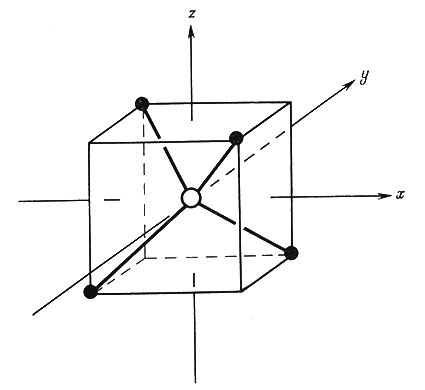
Рис. 11. Тетраэдрический комплекс. Центральный атом расположен в центре куба

Расщепление кристаллическим полем d-орбит для тетраэдрической структуры наглядно изобразить труднее. Во-первых, следует мысленно представить себе тетраэдр, вписанный в куб (рис. 11), так что четыре вершины тетраэдра расположены в четырех вершинах куба. Если теперь провести оси x, y и z таким образом, что они пройдут через центр куба и через центры шести его граней, то можно представить себе положение четырех лигандов относительно d-орбит центрального атома. d-Орбиты, простирающиеся вдоль декартовых осей (d_x²-y² и d_z²), больше удалены от четырех лигандов, чем орбиты, расположенные между осями (d_xy, d_xz, d_yz). Поэтому e_g-орбитам (d_x²-y² и d_z²) соответствует в тетраэдрических комплексах меньшая величина энергии; t_2g-орбиты (d_xy, d_xz, d_yz) характеризуются более высоким значением энергии. Было обнаружено, что разность в величинах энергии e_g- и t^2g-орбит, т. е. расщепление кристаллическим полем Δ_t, составляет только половину Δ₀. Следовательно, эффект кристаллического поля способствует образованию октаэдрических комплексов в большей степени, чем тетраэдрических.

Магнитные свойства комплексов переходных металлов хорошо объясняются теорией кристаллического поля. Переходные металлы имеют частично заполненные d-под-уровни электронов, на которых по правилу Хунда будут находиться неспаренные электроны. Например, ион металла, содержащий три d-электрона (называемый d³-системой), может иметь три неспаренных электрона 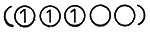а ион металла, содержащий восемь d-электронов, может иметь два неспаренных и три пары электронов 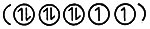Вещества, содержащие неспаренные электроны, притягиваются магнитом, и их называют парамагнитными. (Это притягивание значительно слабее того, которым характеризуются ферромагнитные материалы, такие, как железо.) Величина притяжения веществ к магниту определяется числом имеющихся неспаренных электронов.

Парамагнетизм можно измерить относительно простым способом посредством весов Гуи. Образец помещают в трубку, подвешенную на весах, и измеряют вес образца при наличии и в отсутствие магнитного поля. Если вещество парамагнитно, то вес его возрастет, когда наложится притягивающее действие магнитного поля. Увеличение веса является мерой числа неспаренных электронов в соединении.

Было обнаружено, что некоторые комплексы переходных металлов не подчиняются правилу Хунда. Например, некоторые комплексы Со(III), имеющие электронную конфигурацию d⁶, такие, как [Со(NH₃)₆]³⁺, не притягиваются магнитом (они диамагнитны). Комплексы, в которых несколько неспаренных электронов газообразного иона металла спариваются, называют низкоспиновыми комплексами. Комплекс Co(III) [CoF₆]^3- парамагнитен и имеет четыре неспаренных электрона. Это пример высокоспинового комплекса. В таком комплексе распределение электронов в закомплексованном ионе металла подобно тому, которое наблюдается для газообразного иона. Распределение электронов для этих двух комплексов можно представить следующим образом: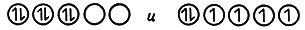

Свойство комплекса, для которого использованы термины "высокоспиновый" и "низкоспиновый", имеет много названий. Они суммированы в примере (16).

Теперь необходимо понять, почему электроны в таких системах распределяются по d-орбитам различным образом. Прежде всего нужно признать, что распределение электронов определяется двумя факторами. Во-первых, в соответствии с правилом Хунда электроны стремятся остаться неспаренными. Чтобы заставить электроны спариться, требуется энергия, достаточная для преодоления сил отталкивания двух электронов, занимающих одну и ту же орбиту. Во-вторых, в кристаллическом поле d-электроны стремятся занять орбиты с низкими значениями энергии и, таким образом, избежать, насколько возможно, отталкивающего действия лигандов. Если устойчивость, достигнутая таким образом (Δ), достаточно велика, чтобы преодолеть потерю устойчивости при спаривании электронов, последние соединятся и в результате получится комплекс низкоспинового типа. Когда расщепление кристаллическим полем (Δ) недостаточно, электроны остаются неспаренными и возникает высокоспиновый комплекс. На рис. 12 показано, что величина Δ₀ для [CoF₆]^3- меньше, чем для [Со(NH₃)₆]³⁺. Комплексы, у которых величина Δ велика, будут в основном низкоспиновыми комплексами. Несколько других примеров расщепления кристаллическим полем и распределения электронов в комплексах приведены на рис. 13.

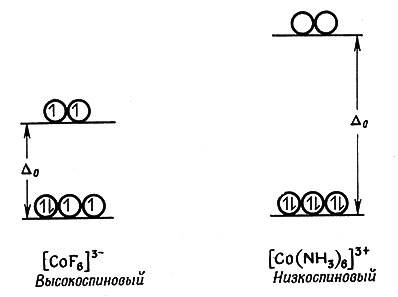
Рис. 12. Относительные величины расщепления кристаллическим полем (Δ₀) d-орбит высокоспиновых и низкоспиновых октаэдрических комплексов Co(III)

Как следует из сказанного выше, величина расщепления кристаллическим полем определяет, спариваются ли d-электроны в ионе металла или подчиняются правилу Хунда. Эта величина влияет и на многие другие свойства переходных металлов. Степень расщепления кристаллическим полем зависит от нескольких факторов. Особенно существенной является природа групп (лигандов), обусловливающих кристаллическое поле. В соответствии с электростатическими представлениями наибольшее расщепление будут вызывать лиганды с большим отрицательным зарядом и лиганды, способные близко подойти к иону металла (небольшие ионы). Небольшие высокозаряженные ионы при приближении к d-орбите делают ее энергетически неблагоприятной для электрона. Это подтверждается экспериментальным фактом, что маленькие ионы F^- вызывают более значительное расщепление кристаллическим полем, чем большие по объему ионы Cl^-, Br^- и I^-.

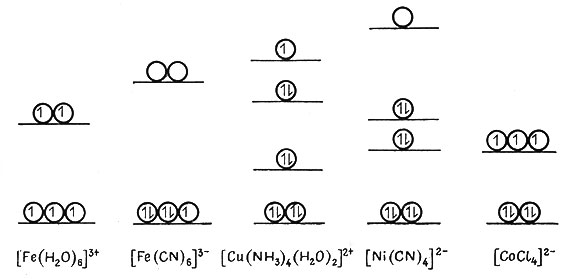
Рис. 13. Расщепление кристаллическим полем и распределение электронов по уровням для некоторых комплексов. Первые два комплекса имеют октаэдрическую структуру, другие (слева направо) - тетрагональную структуру плоского квадрата и тетраэдрическую (рис. 10)

Поскольку расщепление кристаллическим полем является результатом сильного взаимодействия лигандов с орбитами, направленными прямо к ним, и слабого взаимодействия с теми из них, которые направлены между ними, то достижению большего расщепления способствует положение, когда лиганд "фокусирует" свои отрицательные заряды на орбиту. Лиганд с одной свободной электронной парой (например, NH₃) с такой способностью представить себе значительно легче, чем лиганды с двумя или большим числом свободных электронных пар (III и IV)

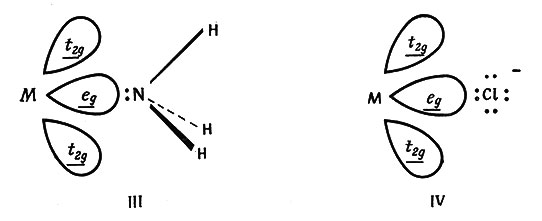
Эту аргументацию можно использовать для объяснения того факта, что нейтральные молекулы NH₃ вызывают большее расщепление кристаллическим полем, чем молекулы воды или отрицательно заряженные ионы галогенов.

В общем, однако, довольно трудно при помощи простой электростатической модели объяснить наблюдаемую способность различных лигандов вызывать расщепление кристаллическим полем. Было найдено, что эта способность уменьшается в приведенном ниже ряду (17). Чтобы объяснить этот ряд, необходимо отказаться от только ионной электростатической модели для связей в комплексах и принять, что ковалентные взаимодействия также существуют.

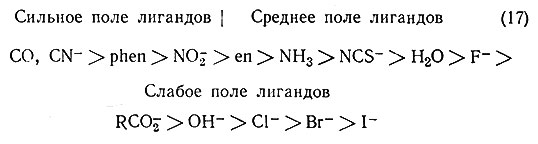
Видоизмененная теория кристаллического поля, предполагающая наличие ковалентной связи в комплексах, называется теорией поля лигандов. Эта теория, по крайней мере качественно, может объяснить величину расщепления кристаллическим полем, обусловливаемого различными лигандами. Такие частицы, как СО, CN^-, phen и NO^-₂, которые создают самое сильное кристаллическое поле, способны образовывать π-связи с центральным атомом металла (разд. 6 гл. II). π-Связь может сильно увеличивать расщепление кристаллическим полем.

На степень расщепления влияет также окислительное состояние иона металла и тип имеющихся у него d-электронов. Более высокая степень окисления иона металла вызывает большее расщепление. Комплекс [Co(NH₃)₆]³⁺ диамагнитен и является низкоспиновым, в то время как [Co(NH₃)₆]²⁺ - парамагнитный высокоспиновый комплекс. Расщепление кристаллическим полем в комплексе Со(III) почти в два раза больше, чем в комплексе Со(II); это объясняется спариванием электронов. Большую величину Δ₀ для Со(III) можно приписать тому факту, что лиганды ближе подходят к меньшему по объему и более высоко заряженному иону металла и, следовательно, более сильно взаимодействуют с его d-электронами. Расщепление кристаллическим полем в комплексах [Rh(NH₃)₆]³⁺ и [Ir(NH₃)₆]³⁺ больше, чем в [Со(NH₃)₆]³⁺. Вообще расщепление больше для комплексов, содержащих 5d-электроны, и меньше для тех, которые содержат 3d-электроны. Этот факт можно приписать тому, что 5d-орбиты простираются в пространстве дальше и, таким образом, сильнее взаимодействуют с лигандами.

Рис. 14. Спектр поглощения комплекса [Ti(H₂O)₆]³⁺. Растворы [Ti(H₂O)₆]³⁺ окрашены в красно-фиолетовый цвет, так как они поглощают желтые лучи, а пропускают синие и красные

Самым большим достижением теории кристаллического поля является успех в объяснении цвета соединений переходных металлов. Следствием сравнительно небольшой разности энергий А между неэквивалентными (t_2g и e_g) d-орбитами в комплексах переходных металлов является то, что переход электрона с более низкого на более высокий уровень энергии может осуществляться за счет поглощения видимого света, что является причиной определен ной окраски комплекса. Например, водный раствор Ti(III) фиолетовый. Цвет объясняется спектром поглощения комплекса [Ti(H₂O)₆]³⁺ (рис. 14). Поглощение комплексом света в видимой области спектра объясняется переходом электрона с орбиты t_2g на её (рис. 15). Спектры поглощения комплексов, содержащих более одного d-электрона, сложнее, так как возможно большее число переходов электронов.

Рис. 15. d-d-Электронный переход, обусловливающий фиолетовую окраску [Ti(H₂O)₆]³⁺.

Уравнение Планка (18) связывает энергию перехода электрона с длиной волны λ абсорбированного света

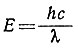
(18)

где h - постоянная Планка (6,62*10^-27 эрг*сек), с - скорость света (3,00*10¹⁰ см/сек). Энергия измеряется в эргах на молекулу, а λ - в сантиметрах. Из уравнения (18) можно определить разность энергии электрона Δ для d-орбит, между которыми осуществляется его переход. Подставляя величины h и с и используя соответствующие факторы пересчета (число Авогадро 6,02*10²³ молекул/моль и постоянную Джоуля 4,18*10⁷ эрг/кал), можно получить формулу (19)

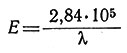
(19)

Здесь Е измеряется в килограммкалориях на 1 моль, а λ - в ангстремах. Было найдено, что максимум в спектре поглощения [Ti(H₂O)₆]³⁺ находится при λ = 5000 ̳; это дает величину разности в энергии между t_2g- и e_g-орбитами около 57 ккал/моль. Расщепление кристаллическим полем, равное 57 ккал/моль, является величиной одного порядка с энергией связи. Несмотря на то что эта величина (57 ккал/моль) несравнимо меньше теплоты гидратации иона Ti³⁺ [уравнение (20)], равной 1027 ккал/моль, она очень важна и необходима для понимания химии переходных металлов

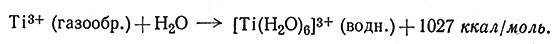
(20)

Следует отметить, что простая ионная модель, на которой основана теория кристаллического поля, не дает четкого представления о связи в соединениях переходных металлов. Имеется много экспериментальных доказательств, подтверждающих, что важную роль играют обе связи: ионная и ковалентная. Тем не менее ионная теория кристаллического поля дает простую модель, которая объясняет многие свойства переходных металлов и которая приводила и будет приводить к постановке многих экспериментов. Роль теории кристаллического поля для объяснения структуры, устойчивости и реакционной способности комплексов обсуждается в следующих главах.