
Перенос электронов в системе с гомогенным распределением переносчиков
Рассмотрим систему, в элементарном объеме которой гомогенно распределены все участники электронотранспортного процесса, причем переносчики электрона обладают относительной подвижностью и способны обмениваться электронами друг с другом. Кинетическая модель электронотранспортного процесса должна включать стадию переноса электронов от донора на белковый переносчик, стадию транспорта электронов между белковыми переносчиками и завершающую стадию переноса электронов на конечный акцептор. "Элементарная" стадия переноса электрона представляет собой бимолекулярную окислительно-восстановительную реакцию
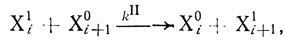 (3.16)
(3.16)где kII - константа скорости второго порядка.
Скорости взаимодействия между переносчиками определяются произведением концентраций восстановленной формы и окисленной формы Хi+1. Например, простейшая кинетическая схема электронного транспорта с участием трех переносчиков электрона имеет такой вид:
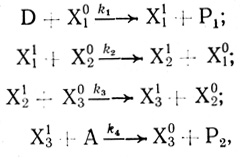 (3.17)
(3.17)где D и А - соответственно донор и акцептор электрона; X10, Х11, Х20, Х21, Х30, Х31 - окисленные и восстановленные формы переносчиков. Для этой модели в стационарном состоянии задача сводится к решению системы нелинейных алгебраических уравнений, которая в некоторых случаях с определенной погрешностью может быть аппроксимирована линейной системой. Анализ такого рода систем уравнений дан в работе [466].
Так, при высоких, "насыщающих" концентрациях донора и акцептора максимальная скорость переноса электрона имеет вид
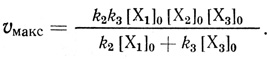 (3.18)
(3.18)Скорость реакции не зависит от концентрации донора и акцептора и определяется константами скорости переноса электрона между переносчиками. При этом важны два частных случая:
1) 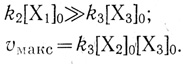 (3.19)
(3.19)
Скорость процесса в этом случае определяется взаимодействием переносчиков Х2 и Х3.
2) 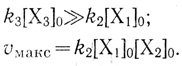 (3.20)
(3.20)
Скорость процесса в целом определяется кинетикой обмена электронами между переносчиками X1 и Х2.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'