
Перенос электрона по цепям структурно-связанных переносчиков
Применимость моделей с гомогенным распределением переносчиков весьма ограничена. Биохимический и структурный анализы электронотранспортной митохондриальной дыхательной цепи показывают, что переносчики электрона в цепи действуют не изолированно, а объединены в специфические комплексы достаточно строгого состава и структуры [20]. Внутренняя митохондриальная мембрана содержит ансамбли переносчиков (оксисомы), действующие в значительной степени независимо друг от друга.
Аналогично фотосинтетическая единица в механизме фотосинтеза содержит определенное число достаточно структурированных переносчиков электрона. Тем не менее известные в литературе модели переноса электронов в биологических системах представляют электронный транспорт как последовательность реакций второго порядка [476-479]. Ограничения в подвижности переносчиков пытались учесть введением специальных стерических коэффициентов. Основное предположение, которое заложено в построении такого рода моделей, заключается в том, что окисленная и восстановленная формы двух соседних переносчиков электрона распределены случайным, статистическим образом относительно друг друга. В этом случае скорость переноса электрона между двумя переносчиками имеет характер реакции второго порядка или в другой форме [480, 481]
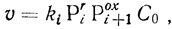 (3.21)
(3.21)где Рir - доля восстановленной формы i-го переносчика; Poxi+1 - доля окисленной формы (i+1)-го переносчика; С0 - общая концентрация цепей.
Использование уравнения (3.21) для описания кинетики электронного транспорта в реальных системах приводит к необходимости вводить в кинетическом смысле достаточно необоснованное предположение, согласно которому константа скорости переноса электрона является функцией общей скорости реакции.
Пониманию кинетических закономерностей электронного транспорта способствовало осознание того факта, что для цепи переноса электрона в комплексе переносчиков кинетическое описание принципиально отличается [466, 475]. Скорость реакции переноса электрона в этом случае не зависит от объемной концентрации восстановленного или окисленного переносчика, а определяется скоростью внутрикомплексного переноса электрона
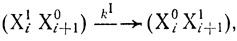 (3.22)
(3.22)где kI - константа скорости первого порядка. Единицей обозначена локализация электрона на переносчике. В процессе, реакции переноса электрона он может быть локализован на активном центре любого переносчика цепи. При этом каждая данная электронотранспортная цепь может иметь различную заселенность электронами. Таким образом, в реакции принимают участие различные частицы, соответствующие различным состояниям электронотранспортной цепи. Например, в простейшей схеме с участием двух переносчиков электрона такого рода состояний четыре: Х10Х20, Х11Х20, Х10Х21, Х11Х21. Последняя частица представляет собой цепь, полностью "заселенную" электронами. Естественно, что кинетические свойства цепей в различном состоянии в общем случае могут различаться и способны характеризоваться различающимися "элементарными" константами скорости процессов переноса электрона.
Рассмотрение в общем виде кинетики электронного транспорта в комплексе переносчиков электрона в цепи произвольной длины - достаточно громоздкая задача. Число возможных состояний цепи N быстро увеличивается с ростом участников электронотранспортного процесса. В общем виде число N для цепи из n переносчиков можно вычислить по уравнению
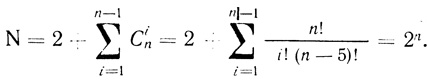 (3.23)
(3.23)Так, для цепи из трех переносчиков электрона N = 8, для системы пяти переносчиков - N = 32.
Изменение во времени каждого состояния электронотранспортной цепи можно описать соответствующим дифференциальным уравнением. С учетом уравнения материального баланса число независимых переменных, описывающих поведение системы, будет равно N-1. В условиях, когда концентрация первичного донора и конечного акцептора существенно превышает общую концентрацию цепей, все дифференциальные уравнения будут линейны. Таким образом, для цепей, составленных из n переносчиков электрона, задача сводится к решению системы (N-1) линейных дифференциальных уравнений первого порядка. Соответственно общее решение этой системы уравнений будет представлено суммой (N-1) экспоненциальных членов.
На первый взгляд задача кажется чрезвычайно сложной, однако в большинстве случаев условия проведения эксперимента позволяют существенно упростить ее решение. Рассмотрим более подробно простейшую систему, состоящую из двух переносчиков электрона. Схему переноса электрона в системе с участием двух структурно связанных переносчиков можно представить в виде:
D + Х01Х20 k1→ Х11Х20 + Р1; (3.24)
D + Х01Х21 k2→ Х11Х21 + Р1; (3.25)
Х11Х20 k3→ Х10Х21; (3.26)
A + Х10Х21 k4→ Х10Х20 + Р2; (3.27)
A + Х11Х21 k5→ Х11Х20 + Р2, (3.28)
где D и А - донор и акцептор электрона электронотранспортной цепи соответственно; P1 и Р2 - продукты превращения донора и акцептора; Х10Х20, Х11Х20, Х10Х21, X11X21 - различные возможные состояния электронотранспортной цепи. Для простоты предполагается, что все стадии практически необратимы. Кинетику процесса в условиях [D] >> [X0], [А]0 >> [Х]0 описывает система четырех связанных уравнений:
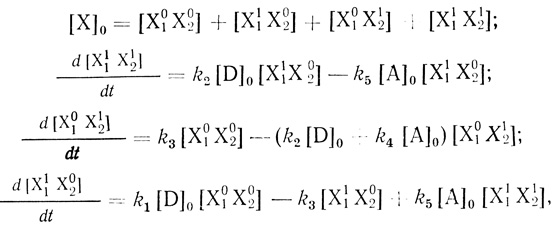 (3.29)
(3.29)где [X]0 - общая концентрация цепей.
Уравнения (3.29) представляют собой систему линейных дифференциальных уравнений с постоянными коэффициентами. Аналитическое решение такого рода систем применительно к задачам химической и ферментативной кинетики подробно рассмотрено в [252, 254]. Характеристическое уравнение системы представлено уравнением третьего порядка:
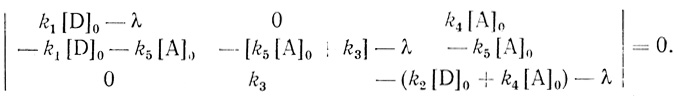 (3.30)
(3.30)Соответственно кинетика процесса описывается суммой трех экспоненциальных членов, показатели экспонент которых есть обратные корни характеристического уравнения
τ1, 2, 3 = -1/λ1, 2, 3. (3.31)
При этом характеристические времена являются сложными функциями констант скоростей "элементарных" стадий переноса электрона (см. [254, 466]).
В ряде случаев кинетика процесса существенно упрощается. Например, в условиях, когда концентрация акцептора равна нулю, определитель (3.30) диагонализуется, и корни характеристического уравнения соответственно равны:
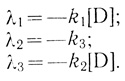 (3.32)
(3.32)Очевидно, когда скорость акцептирования электрона электронотранспортной цепью не зависит от степени ее заселенности (k1 = k2), кинетика процесса описывается двумя "временами релаксации".
Аналогично можно показать, что в условиях, когда в системе концентрация донора равна нулю (цепь предварительно заселена электронами), наблюдаемые характеристические времена реакций даются следующими уравнениями:
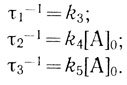 (3.33)
(3.33)Нестационарный подход широко используется при анализе кинетики и механизма электронного транспорта в фотосинтетической цепи. Реакцию обычно инициируют быстрым импульсом света, который "эжектирует" электроны из реакционных центров в электронотранспортные цепи. Таким образом, была изучена кинетика окисления цитохромов в электронотранспортной цепи Chromatium [467], электронный транспорт между пластохиноном и хлорофиллом Р700 [468] и некоторые другие реакции. Наблюдаемые кинетические кривые в большинстве случаев достаточно строго описываются экспоненциальными уравнениями. Это подтверждает, что реакция представляет собой внутрикомплексный перенос электрона, а не бимолекулярную реакцию взаимодействия переносчиков (см. выше модель с гомогенным распределением переносчиков). Обычно авторы постулируют, что регистрируемые характеристические времена отражают элементарный процесс окисления или восстановления того или иного переносчика. Как следует из приведенного примера переноса электронов в комплексе двух переносчиков электрона, это предположение имеет кинетическое обоснование.
После протекания процесса в нестационарных условиях система переходит в стационарный режим, в котором устанавливаются постоянные концентрации цепей в различном состоянии. Система дифференциальных уравнений, описывающая кинетику процесса, трансформируется в систему линейных алгебраических уравнений, решение которой дает концентрации электронотранспортных цепей в различном состоянии заселенности электронами [466]. Стационарная скорость переноса электрона на конечный акцептор является аддитивной функцией стационарной концентрации цепей в различном состоянии с локализацией электрона на последнем переносчике. Для реакций с участием различного числа переносчиков электрона в работах [465, 466, 474] были получены зависимости стационарной скорости процесса от концентрации исходного донора и конечного акцептора, а также от степени восстановленности переносчиков цепи. Детальное описание систем уравнений и техника получения решений даны в работе [466].
Так, для системы двух переносчиков электронов стационарная скорость реакции равна
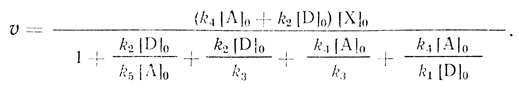 (3.34)
(3.34)В работе [474] проведено сравнение модели электронного транспорта с гомогенным распределением переносчиков и модели комплексов переносчиков. В результате анализа удалось выделить как инвариантное свойство цепи переноса электрона, не зависящие от использованной модели, так и некоторые особенности кинетики процессов, позволяющие дискриминировать механизмы реакций.
Зависимость стационарной скорости процесса от концентрации как исходного донора, так и конечного акцептора, в рамках обеих моделей представляет собой функцию, асимптотически приближающуюся к предельной скорости электронного транспорта. При бимолекулярных стадиях донирования в цепь и акцептирования электронов из цепи предельная максимальная скорость определяется стадией электронного обмена между переносчиками цепи.
Существует одна особенность систем переносчиков электрона, объединенных в комплексы, которая в принципе позволяет дискриминировать механизмы на основе анализа экспериментальных данных кинетики. Изложенные выше модели процессов электронного транспорта могут быть разграничены в том случае, если кинетические свойства переносчиков, объединенных в комплекс, окажутся чувствительными к окислительно-восстановительному состоянию соседних переносчиков в цепи. Например, константа скорости акцептирования электрона переносчиком Хi зависит от того, в каком состоянии - окисленном или восстановленном - находится переносчик Xi+1.
В общем случае константа скорости акцептирования электрона, например, переносчиком X1 в комплексе может зависеть от того, свободна или полностью "заселена" электронами данная электронотранспортная цепь. Фактор электронного влияния, который можно определить как отношение констант скоростей элементарной стадии акцептирования (или донирования) электрона для двух состояний цепи, может отличаться от единицы.
Если фактор электронного влияния существенно превышает единицу, из рассмотрения кинетики процесса следует, что можно наблюдать высокие порядки регистрируемой скорости электронного транспорта от концентрации субстратов или суммарной степени восстановленности переносчиков электрона. В условиях, когда скорость процесса не лимитирована стадиями переноса электронов на конечный акцептор и стадиями переноса электронов внутри цепи, зависимость стационарной скорости процесса от степени восстановленности i-го переносчика дается уравнением
υ = αРxi⋅n/n-i+1, (3.35)
где n - число переносчиков в цепи; Pxi - степень восстановленности переносчика.
Таким образом, при данном числе переносчиков электронотранспортной цепи можно получить теоретическую последовательность показателей степеней зависимости скорости процесса от доли восстановленности каждого переносчика цепи. В табл. 28 приведены теоретические показатели степеней уравнения для электронотранспортных цепей с различным числом переносчиков.

Таблица 28
Максимально возможный порядок по степени восстановления последнего переносчика соответствует числу переносчиков, объединенных в цепь, при этом для последнего переносчика должна наблюдаться линейная зависимость скорости процесса от степени его восстановленности. Такого рода эффекты действительно могут быть обнаружены экспериментально.
Как следует из уравнения (3.35), зависимость стационарной скорости процесса от степени восстановленности того или иного переносчика представляет собой степенную функцию, показатель которой определяется общим числом переносчиков цепи n и местом данного переносчика в последовательности элементарных актов переноса электрона i. Сложная зависимость скорости процесса от степени восстановленности переносчиков обнаружена в работе [482]. На рис. 39 приведены экспериментальные данные этой работы, трансформированные в форму уравнения (3.35).
![Рис. 39. Зависимость стационарной скорости реакции переноса электронов от НАДН к кислороду с участием электронотранспортной цепи субмитохондриальных частиц от степени восстановленности переносчиков (экспериментальные данные Сакса В. с соавторами [482]). Цитохромы: 1 - а3; 2 - а; 3 - с; 4 - с1; 5 - b](pic/000219.jpg)
Рис. 39. Зависимость стационарной скорости реакции переноса электронов от НАДН к кислороду с участием электронотранспортной цепи субмитохондриальных частиц от степени восстановленности переносчиков (экспериментальные данные Сакса В. с соавторами [482]). Цитохромы: 1 - а3; 2 - а; 3 - с; 4 - с1; 5 - b
Показатели степеней m, полученные для различных переносчиков цепи (из рис. 39), даны в табл. 29. Показатели степенных зависимостей располагаются строго в соответствии с последовательностью стадий переноса электрона в электронотранспортной цепи. В таблице также приведены теоретические последовательности показателей степеней для цепей с числом переносчиков 9, 10 и 11. Экспериментально наблюдаемая последовательность хорошо согласуется с теоретически предсказанной. Эти данные позволяют приближенно оценить общее число участников электронотранспортной цепи, которое лежит в диапазоне 8-12. Таким образом, кинетическая модель достаточно хорошо описывает стационарную кинетику электронного транспорта в митохондриях и обладает определенной предсказательной силой.

Таблица 29
На основании проведенного нами кинетического анализа показано, что в реакции переноса электрона от НАДН на кислород с участием электронотранспортной цепи митохондрий фактор электронного влияния существенно превышает единицу. На основании кинетических данных найдено, что цепь переноса электрона в митохондриях функционирует как комплекс 9-12 переносчиков электронов. При этом цепь, "заселенная" электронами, является наиболее активным катализатором электронного транспорта. Проведенный кинетический анализ дает молекулярно-кинетическое толкование наблюдаемых ранее эффектов активации электронотранспортной цепи функционированием. Образование пула электронов в электронотранспортной цепи приводит к появлению новых кинетических свойств системы.
Каков физический механизм этого эффекта? Каким образом образование пула электронов в электронотранспортной цепи приводит к увеличению кинетических доноро-акцепторных свойств системы? Можно представить себе несколько механизмов этого явления. В общем случае "активация" связана, по-видимому, с комплексом структурных изменений электронотранспортной цепи при восстановлении переносчика. Появление в системе некомпенсированного электрона вызывает сильную поляризацию среды. На этом основаны современные представления о механизме реакции переноса электрона в растворах [484-486].
В полимерной белковой среде это может вызвать специфические термодинамически невыгодные конформационные изменения, обладающие сравнительно большими временами релаксации в исходное состояние [487-489]. В этой ситуации могут возникнуть условия, обеспечивающие перенос нескольких (или потока) электронов, прежде чем цепь релаксирует в исходное состояние за счет теплового движения. По своей физической картине, но не по глубине эффектов, данный механизм близок к механизму, предложенному Литтлом [490, 491] при обсуждении сверхпроводимости в органических полимерных полупроводниках. По-видимому, кооперативная "активация" электронотранспортной цепи "заселением" ее электронами отражает фундаментальные особенности процессов переноса электронов в полимерных средах.
Эффекты влияния "заселенности" цепи на кинетические характеристики электронного транспорта наблюдаются также при исследовании электронотранспортной цепи фотосинтеза. Нами экспериментально исследована стационарная кинетика переноса электронов от воды на искусственные акцепторы электронотранспортной цепи фотосинтеза. В качестве экзогенно добавленных акцепторов использованы феррицианид калия и бензохинон. Были изучены зависимости начальной стационарной скорости фотовосстановления акцепторов от их концентрации, интенсивности поглощаемого света, концентрации ионов водорода, температуры. Стационарный процесс электронного транспорта характеризуется следующими основными закономерностями:
1. Зависимости скорости реакции от концентрации акцепторов и интенсивности света представляют собой функции с "насыщением" (рис. 40). Использование высоких концентраций акцептора и высоких интенсивностей света выводит систему на предельный режим, в котором скорости процесса не зависят от переменного параметра.
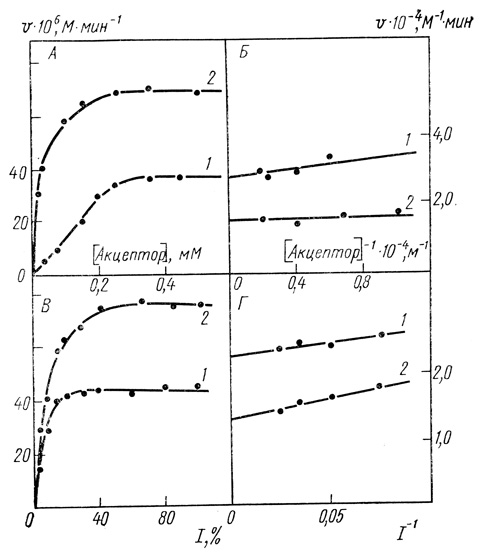
Рис. 40. Зависимость начальной стационарной скорости фотовосстановления экзогенных акцепторов от концентрации акцепторов (А, Б) и интенсивности света (В, Г); 20 мМ МЭС; 0,4 М сахарозы; 10 мМ хлористого натрия; pH 9,2; 25°С
2. Зависимости скорости от концентраций ионов водорода представляют собой pH-функции достаточно сложного вида (рис. 41), при этом pH-зависимость максимальной скорости процесса зависит от интенсивности поглощаемого света. При переходе от низких интенсивностей к высоким наблюдается существенное изменение ионогенных групп, контролирующих скорость переноса электронов.
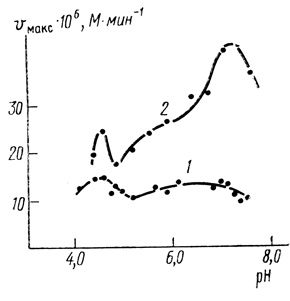
Рис. 41. Влияние pH на максимальную скорость фотовосстановления феррицианида калия: 1 - 'насыщающая' интенсивность света; 2 - интенсивность света в 40 раз меньшая; 0,6 мМ K3Fe(CN)6; 10 мМ МЭС; 10 мМ трицин; 0,4 М сахароза, 10 мМ NaCl, 25°С
Полученные результаты находят объяснение в рамках развитой выше модели электронного транспорта с участием цепей переноса электрона. Рассмотрим реакцию переноса электрона в системе с двумя переносчиками, учитывая участие в механизме реакции цепей с различной степенью протонированности переносчиков. Для фотосинтетических цепей донирование электронов в цепь осуществляется светом, соответственно процесс донирования можно представить в виде
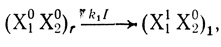 (3.36)
(3.36)где (X10X20)r - частица в реакционноспособной форме; (Х11Х20)n - частица после переноса электрона, которая может отличаться по протонированности от частицы (Х11Х20)r, принимающей участие в последующем превращении.
Процесс "уравновешивания" частиц по протонированным состояниям можно представить следующим образом:
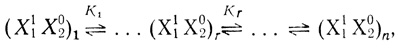 (3.37)
(3.37)где каждая стадия характеризуется своей константой равновесия. Частица (X11X20)r принимает участие в дальнейшем процессе:
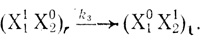 (3.38)
(3.38)Концентрацию реакционноспособной частицы (X11X20)r можно вычислить по уравнению
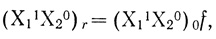 (3.39)
(3.39)где (Х11Х20) - общая концентрация цепей данной степени заселенности; f - доля реакционноспособных частиц.
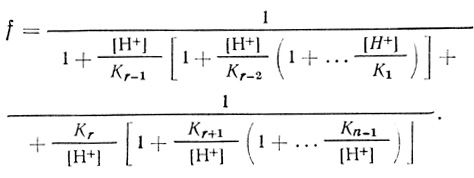 (3.40)
(3.40)Соответственно для каждой из частиц, принимающих участие в механизме (3.17), можно записать:
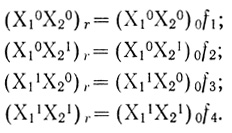 (3.41)
(3.41)Уравнение стационарной скорости реакции будет иметь вид
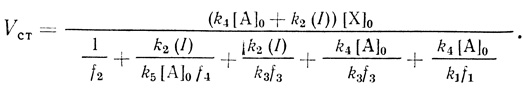 (3.42)
(3.42)Результаты анализа полученного уравнения в предельных условиях:
1. При очень низких интенсивностях света (I → ∞) стационарная скорость процесса определяется скоростью донирования электронов
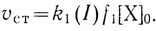 (3.43)
(3.43)2. При высоких интенсивностях света (I → ∞) скорость процесса не зависит от интенсивности света и выходит на предельный уровень
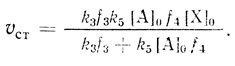 (3.44)
(3.44)3. Если реакция протекает при низких концентрациях акцептора ([А]0 → 0)
υст = k5[A]0f4[X]0 (3.45)
скорость процесса определяет стадии акцептирования электронов из цепи.
4. Высокие концентрации акцептора переводят систему в режим, когда стационарная скорость реакции не зависит от концентрации акцептора и определяется скоростью донирования в электронотранспортную цепь:
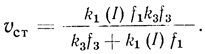 (3.46)
(3.46)5. Важное свойство электронотранспортной цепи заключается в том, что при "насыщении" системы по интенсивности света и концентрации акцептора скорость электронотранспортного процесса определяется белок-белковым переносом по цепи:
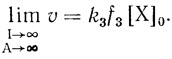 (3.47)
(3.47)Использование различных условий реакции позволяет переводить электронотранспортную цепь в различные состояния по заселенности электронами. Например, при высоких интенсивностях света и низких концентрациях акцептора электронотранспортная цепь полностью "заселена" электронами. Низкие интенсивности света и высокие концентрации акцептора в стационарном состоянии приводят к цепям, практически лишенным электронов. Наконец, использование "насыщающих" интенсивностей и концентраций акцепторов дают цепи, "населенные" электронами до лимитирующей стадии реакции и лишенные электронов после лимитирующего процесса. Очевидно, что функции, описывающие зависимости скорости электронного транспорта от pH для различных условий проведения процесса, должны различаться.
Так, в уравнение скорости при низких интенсивностях света и высоких концентрациях акцептора входит pH-функция f1, при высоких интенсивностях света и "насыщающих" концентрациях акцептора уравнение скорости определяет рН-функции f3. В том случае, если "заселение" цепи электронами приводит к изменению протолитических свойств цепи, изменению констант ионизации функционально важных ионогенных групп (f1 ≠ f3), должно наблюдаться различие в зависимости скорости от pH для двух режимов проведения процесса. Это различие надо интерпретировать как следствие электронного влияния на протолитическое равновесие в системе.
Данные выводы, количественно полученные для простейшей электронотранспортной цепи, могут быть на качественном уровне распространены на системы с большим числом переносчиков. Высокие концентрации акцептора и низкие интенсивности света приводят к тому, что "разряд" цепи происходит быстрее, чем ее "заселение" электронами, цепь можно представить в виде (Х10Х20 ... Хn0). "Насыщение" системы по свету и использование низких концентраций акцептора приводит к полностью заселенной цепи (Х11Х21 ... Хn1). Если в механизме электронного транспорта имеется одна наиболее медленная стадия, например перенос электрона с переносчика Xi, использование условий "насыщения" системы по донору и акцептору приводит к состоянию, в котором цепь "заселена" электронами до лимитирующего переносчика и лишена электронов после лимитирующей стадии (Х11Х21 ... Хi1Хi+10 ... Хn0).
Из данных, представленных на рис. 40, следует, что при "насыщении" по акцептору и интенсивности света электронотранспортная цепь выходит на предельный режим, в котором скорость процесса определяется переносом электронов в цепи. Представляет интерес численная оценка константы скорости лимитирующей стадии процесса. Если принять, что на одну фотосинтетическую единицу изолированных хлоропластов приходится 400 молекул хлорофилла [493], использование уравнения
υмакс = klim[X]0 (3.48)
приводит для реакции с феррицианидом при pH 8,2 к значению klim = 32 ± 5 с-1. Из данных по нестационарной кинетике электронного транспорта следует, что наиболее медленным процессом в механизме переноса электронов с участием фотосистемы I и фотосистемы II является стадия окисления пластохинона, характеризуемая временем полупревращения 20 мс [494]. Сопоставление этой величины с найденным нами значением константы скорости переноса электрона в стационарных условиях показывает, что эти величины весьма близки. Это позволяет думать, что в стационарном состоянии электронотранспортный процесс также лимитируется окислением пластохинона.
Из данных рис. 41 следует, что "заселение" электронотранспортной цепи существенно изменяет способность ионогенных групп белков - участников процесса - к реакциям присоединения протона. При низких интенсивностях света перенос электрона на лимитирующей стадии проходит по цепи X10X20 ... Х0 ... Хn0, использование "насыщающих" интенсивностей дает цепь Х11Х21 ... Хi1Х0i+1 ... X0n. Таким образом, переносчик, лимитирующий процесс, "чувствует" уровень "заселенности" цепи электронами.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'