
Решение задач, содержащих арифметические расчеты
Расчеты по химическим формулам. Наиболее разработаны способы решения задач, включающих расчеты: 1) по химическим формулам, 2) по уравнениям, 3) на применение газовых законов, 4) связанные с изучением способов выражения концентрации растворов.
Задачи на расчеты по формулам могут быть трех типов.
Первый тип.
1. Нахождение весовых отношений между элементами по формуле сложного вещества.
2. Выражение весового состава вещества в процентах по формуле этого вещества.
3. Тот же тип задач, усложненный тем, что для определения дается смесь, например: "Сколько процентов железа содержится в руде, содержащей 56% окиси железа?"
Второй тип.
Нахождение количества элемента в заданном количестве сложного вещества.
1. Задача того же типа с. применением понятий "грамм-атом" и "грамм-молекула".
2. Задача того же типа, усложненная тем, что для определения дается смесь, например: "Сколько килограммов железа содержится в 1 т руды, содержащей 64% окиси железа?"
Третий тип.
Нахождение количества сложного вещества по заданному количеству элемента. Усложненные задачи.
1. Задачи с использованием понятий "грамм-атома" и "грамм-молекулы".
2. Определение смеси определенного процентного содержания по заданному количеству элемента, например: "В каком количестве руды содержится 224 кг железа, если известно, что в руде находится 64% окиси железа?"
В практике обучения химии принято решать задачи без усложнений в VII классе, а остальные в старших классах.
Некоторые учителя химии затрачивают слишком много времени на обучение учащихся VII класса расчетам по формулам и уравнениям, не добиваясь полного успеха, хотя расчеты по своей простоте значительно ниже возможностей учащихся VII класса, не говоря уже о десятиклассниках. Малая педагогическая эффективность обучения решению задач снижается еще и потому, что применяются не всегда лучшие математические приемы решения задач, о чем будет сказано ниже.
Можно указать еще на одну из причин, задерживающих развитие умений решать задачи.
Учащиеся VII класса далеко не все могут решить такую простую задачу: "Сколько процентов меди содержится в окиси меди СuО?" - если учитель, не объяснял, как нужно решать ее. А в V классе эти же учащиеся на уроках арифметики решали аналогичные задачи, вычисляя в процентах содержание какого-либо компонента смеси, состав которой выражен в весовых частях.
Наблюдая в опыте работы школ другие случаи затруднений учащихся в перенесении навыков, полученных в обучении по одному учебному предмету, в практику учебной работы по другому учебному предмету, можно объяснить описанный выше случай тем, что в сознании учащихся не утвердилась мысль о том, что данная задача, по-существу, арифметическая. Видимо, знания арифметики не достигли надлежащей обобщенности. Если же восстановить логическую связь между отдельными задачами - химическими и арифметическими, то затруднения у учащихся исчезнут.
Справедливость этого объяснения подтверждается опытом.
Учащимся седьмых классов, прежде чем знакомить их с расчетами по формулам, было предложено решить следующую арифметическую задачу: "В колхозе для удобрений полей приготовили смесь - 64 т торфа и 16 г минеральных удобрений. Сколько процентов минеральных удобрений находилось в смеси?" Учащимся не указывали способ решения этой задачи, а предлагали вспомнить и решить тем способом, каким им больше нравится. Все решили эту задачу, применяя разные способы: нахождение части от числа, пропорциональное деление, приведение к единице и составление пропорций. Большинство пользовалось способом нахождения части от числа.
После этого была предложена задача: "Сколько процентов меди в окиси меди, если известно, что формула этого вещества СuО, атомная масса меди 64, кислорода 16?"
Как и следовало ожидать, задача была решена быстро, о чем можно было судить по поднятым рукам учащихся почти всего класса. Затруднения представляли объяснения решения задачи: нужно было добиться по возможности краткого объяснения с включением в него понятий "молекулярная масса". В результате беседы пришли к такому решению: сначала нужно вычислить молекулярную массу вещества, затем определить, какую часть молекулярной массы составляет атомная масса меди. Молекулярная масса находится сложением атомных масс меди и кислорода: 64 + 16 = 80 (к. е.). После этого делится атомная масса меди на молекулярную массу окиси меди
| 64 : 80 = | 64 | . |
| 80 |
Чтобы выразить эту дробь в процентах, т. е. в сотых долях, нужно 100% умножить на эту дробь.
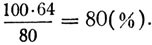
Чтобы закрепить этот способ решения задачи, предложено решить несколько усложненную задачу: "Сколько процентов железа содержится в окиси железа Fe2О3?" Атомная масса железа равна 56. Решение этой задачи заняло несколько больше времени. Некоторые учащиеся допускали ошибки в вычислении молекулярной массы, упустив из внимания индексы. Другие делили на численную величину молекулярной массы вес одного атома железа, а не сумму двух атомов. Но эти ошибки были единичными. Под конец урока было предложено самим учащимся придумать и решить аналогичную задачу. Это задание сначала вызвало недоумение многих учащихся - такого рода задание было ново для них. Но затем они заинтересовались. Этот прием был применен и при решении других типов задач, требующих расчетов по формуле. Учащиеся выполняли все работы самостоятельно, они вспоминали то, что знали из курса арифметики, и применяли эти знания на уроке химии.
Успешное овладение этим методом расчетов по формулам сложных веществ вызвало предположение, что представление о сложности обучения учащихся VII класса вести расчеты по формулам не соответствует действительности. Возможно, что даже, в VII классе нет необходимости так много решать вычислительных задач, как это наблюдается в практике многих учителей химии. Для проверки справедливости этого предположения был предложен педагогический эксперимент в VII классе.
В домашние задания учащихся не включали задачи на расчеты по формулам до 1 мая, а в мае включили решение таких задач в письменную контрольную работу. Результаты работы показали, что учащиеся без значительных затруднений могут производить описанные выше расчеты, если они не усложнены большими числами, сложными вычислениями. Этими опытами было доказано, что для ознакомления учащихся VII класса с расчетами по формулам, если задачи несложные, необходимо и достаточно два урока и затем два-три домашних задания, содержащих расчетные задачи, в течение всего учебного года.
Расчеты по химическим уравнениям. В зависимости от типа химических реакций в задачах, связанных с вычислениями по химическим уравнениям, могут иметь значение количества нескольких веществ, вступающих в реакцию или получающихся в результате реакции. Но для расчета по химическим уравнениям достаточно знать одну какую-нибудь величину: количество одного из вступивших в реакцию веществ или количество веществ, полученных в результате реакции. Такая возможность представляется потому, что количества реагирующих веществ и получающихся в результате реакции связаны стехиометрическими отношениями. Поэтому достаточно рассмотреть способы вычисления по уравнению одного какого-либо типа химических уравнений, чтобы потом перенести эти способы на вычисления по уравнениям других типов реакций.
"Сколько сернистого железа должно получиться, если соединить с железом 64 г серы?" Подготовительные записи: составляют уравнение реакции
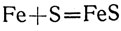
подсчитывают и подписывают значения формул и знаков в углеродных единицах (56 + 32 = 88), подписывают данные из задачи, обозначая искомое количество через х. Далее следуют рассуждения: количество сернистого железа относится к количеству серы как 88 к 32. Следовательно, из заданного количества серы должно получиться сернистого железа в 88/32 раз больше. Решение:
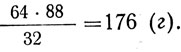
Если бы в задаче требовалось узнать количество железа, соединившегося с заданным количеством серы, то нужно было бы умножить 64 г на весовое отношение количества железа
к количеству серы в сернистом железе, т. е. на
| 56 | , | |
| 32 |
тогда количество железа было бы
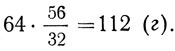
Так как в реакции соединения двух веществ связаны три величины стехиометрическими отношениями, то по одной заданной величине можно определять другие величины. По количеству серы определяют количество железа и сернистого железа, по количеству сернистого железа определяют количество серы и железа в отдельности.
Эти рассуждения можно представить в общем виде. Если дано количество А вещества, имеющего атомную массу а, и требуется узнать х - количество вещества, которое должно соединиться с ним, и атомная или молекулярная масса его б, тогда
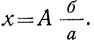
Если требуется узнать, какое количество вещества х1 имеющего молекулярную массу с, должно получиться в результате реакции, то
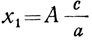
Аналогичные рассуждения применимы и при расчетах по уравнениям реакций замещения, разложения и обмена, например: "Сколько граммов меди выделится из раствора хлорной меди при переходе в раствор 112 г железа?" Уравнение реакции:
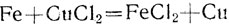
В этой задаче нужно определить весовые отношения железа и меди по уравнению реакции. Это отношение в данном случае равно отношению атомных масс меди и железа (64 к 56). Количество меди х, которое должно выделиться из раствора, равно заданному количеству железа 112 г, умноженному на это отношение:
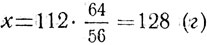
Как видим, для расчетов по уравнению реакции нет необходимости в составлении пропорции.
Расчетные задачи по теме "Концентрация растворов". Расчеты, которые производятся при решении этих задач, основаны на знаниях учащихся по математике по программе V-VI классов. Казалось бы, что для обучения решать эти задачи не потребуется много времени. На практике же учащиеся решают задачи по преимуществу дома, и результаты получаются не очень хорошие. Одна из причин малой производительности учебного труда состоит в том, что учащиеся не всегда знакомы с общими способами решения однотипных задач и не пользуются обобщенными (алгебраическими формулами) для расчетов при их решении. Например, учащиеся VII класса знакомятся с разными вариантами задач, в которых требуется нахождение количества растворенного вещества, либо растворителя, либо концентрации, не устанавливая математической связи между этими величинами. А эта зависимость дается в определении понятия концентрации, если оно (понятие) правильно сформулировано. Концентрацией растворов называется отношение количества растворенного вещества к количеству раствора или к количеству растворителя. В химии принято относить количество растворенного вещества к количеству раствора. Это отношение можно выразить следующей математической формулой (1):
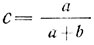
а - количество растворенного вещества, b - количество растворителя, с - концентрация раствора. Так как в этой формуле связаны три величины, то и задачи могут быть трех типов: нахождение концентрации, количества растворенного вещества и количества растворителя.
Первый тип.
Нахождение концентрации. Сколько, процентов соли содержится в растворе, если известно, что 20 г соли растворено в 60 г воды?
Подставив в уравнение 1 значение а (20) и b (60), получим
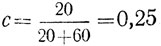
Чтобы выразить концентрацию в процентах, следует 100% умножить на эту дробь (2):
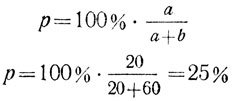
Второй тип.
Определение величины а - количества растворенного вещества. Сколько граммов соли нужно растворить в 60 г воды, чтобы получить 25-процентный раствор?
Для решения этого типа задач нужно преобразовать уравнение 2 так, чтобы а было в левой части уравнения (3):
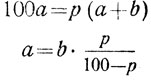
Подставив в уравнение 3 значение b и р, получим количество растворенного вещества:
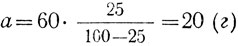
Третий тип.
Определение количества растворителя. Для этого преобразуем уравнение 3, перенеся b в левую часть уравнения (4):
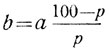
В каком количестве воды нужно растворить 20 г соли, чтобы получить 25-процентный раствор?
Подставив значение а и p в уравнение 4, получим количество растворителя:
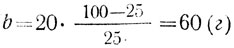
Из приведенных примеров видно, насколько упрощаются вычисления при решении всех трех типов задач, если пользоваться приведенными выше уравнениями. Выведение самих формул из основной (1) не представляет каких-либо трудностей для учащихся VII класса. Первая же формула является математическим выражением определения концентрации растворов.
На практике часто приходится разбавлять растворы до заданных концентраций. При этом к более концентрированному раствору добавляется менее концентрированный раствор или вода. Например, требуется узнать, в каких весовых отношениях нужно взять 40-процентный и 10-процентный растворы, чтобы получить 30-процентный раствор.
Для решения этой задачи обозначим количество первого раствора через х, второго через у, третьего через z. Тогда количество растворенных веществ в первом растворе должно быть
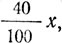
а количество растворенного вещества во втором растворе
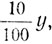
а в третьем
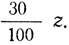
Так как количество растворенного вещества в первых двух растворах равно количеству растворенного вещества в новом растворе, полученном от смешения первых двух, то можно записать уравнение:
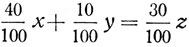
или после умножения членов уравнения на 100 (5):
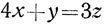
Но количество полученного раствора равно сумме количеств смешанных растворов, т. е.
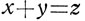
Подставим в уравнение 5 вместо z сумму х+у и получим:
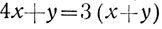
или
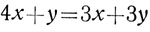
После перенесения 3х в левую часть, а у - в правую получим уравнение:
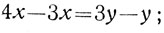
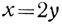
или
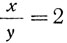
Следовательно, 40-процентного раствора нужно взять в два раза больше, чем 10-процентного. Последнюю математическую формулу можно прочесть так: отношение количества первого раствора (х) к количеству второго раствора (у) равно отношению разности между концентрациями третьего и второго растворов (0,3-0,1) к разности концентраций между первым и третьим раствором (0,4-0,3). Эту формулу графически можно выразить так:
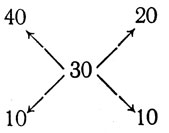
Отношение 20:10 или 2:1 показывает отношение между количеством первого 40-процентного и второго 10-процентного растворов. Эта простая схема позволяет быстро решать задачи и указанного ниже содержания.
Сколько граммов 40-процентного раствора нужно добавить к 50 г 10-процентного раствора, чтобы получить 20-процентный раствор?
Решение. Находим весовые отношения между первым и вторым раствором:
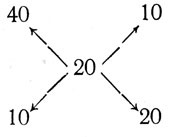
Это отношение равно
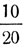
или
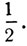
Это значит, что первого (40%) раствора нужно взять в два раза меньше, чем второго, т. е.
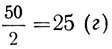
Сколько граммов воды нужно добавить к 60 г 40-процент-ного раствора, чтобы получить 10-процентный раствор?
Решение. Находим отношение между количествами первого раствора и воды:
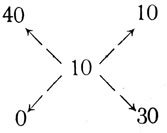
Схема показывает, что воды нужно взять в три раза больше, чем 40-процентного раствора, т. е. 60 г · 3 = 180 г.
В рекомендуемых нами способах вычислений при решении химических задач видное место отводится разнообразным арифметическим приемам и математическим формулам. Некоторые из учителей химии высказывают сомнение, могут ли учащиеся VII класса и старших классов усваивать вывод приведенных выше математических формул и сознательно пользоваться ими. Положительный ответ на этот вопрос можно получить, ознакомившись с программой по математике. Второе возражение направлено против широкого использования математических формул вообще при обучении химии. Обосновывается это тем, что в случае применения формул учащиеся якобы механически решают задачи. В этом возражении проявляется непонимание роли математики с ее формулами в системе общего образования. Одна из основных задач обучения математике состоит в вооружении учащихся знаниями и умениями быстро вычислять, пользуясь этими знаниями математических формул.
Для преподавания химии особенно важно устранить в решении химических задач трудности математического характера и выдвинуть на первый план химическую сторону в упражнениях и задачах.
Как уже отмечалось выше, практика показывает, что при наличии даже хорошего задачника учителям приходится составлять дополнительно задачи по разным разделам курса химии. Не менее важно вводить в практику обучения составление химических задач самими учащимися. В преподавании химии этот способ встречается редко. Но там, где им пользуются, он приносит хорошие результаты, если не злоупотреблять им и не перегружать учащихся избыточными задачами, в которых превалирует арифметика.
О методике обучения учащихся решать качественные экспериментальные задачи сказано в параграфе об использовании ученического эксперимента в процессе обучения применению знаний.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'