§ 6. Точечные и пространственные группы симметрии

Совокупность операций симметрии, которые можно выполнить на одной и той же фигуре, называют группой симметрии. Группы симметрии, составленные из одних закрытых операций, называются точенными. Точечные группы описывают все возможные случаи симметрии конечных фигур, в частности молекул. Группы симметрии, составленные как из закрытых, так и открытых операций, действующих во всех трех измерениях пространства, называют пространственными. Именно эти группы описывают все возможные случаи симметрии кристаллических структур.

Хотя специально мы не останавливаемся на правилах сопряжения разных элементов симметрии, обратим все же внимание на три наиболее важных случая, касающихся точечных групп симметрии.

1. Поворотная ось симметрии любого порядка (на рис. 10, а взята в качестве примера ось симметрии четвертого порядка) и перпендикулярная ей ось симметрии второго порядка порождают и другие оси симметрии второго порядка, также перпендикулярные главной оси; их число равно порядку главной оси.
2. Поворотная ось симметрии любого порядка (на рис. 10, б снова ось четвертого порядка) и параллельная ей плоскость зеркального отражения порождают и другие плоскости зеркального отражения, также параллельные главной оси; их число снова равно порядку главной оси.
   
   Рис. 10. Некоторые точечные группы на основе поворотной оси четвертого порядка
   
   
   Ось 4 (в центре рисунка) направлена перпендикулярно плоскости рисунка; двойные линии - плоскости зеркального отражения, одинарные - поворотные оси второго порядка. Кружки - фрагменты фигуры, расположенные над плоскостью проекции, крестики - фрагменты фигуры под плоскостью проекции (на таком же расстоянии)
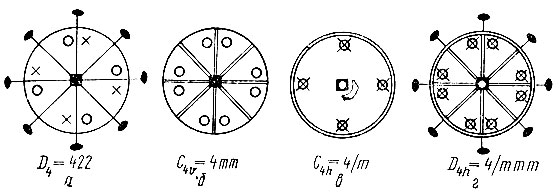
3. Поворотная ось симметрии четного порядка и перпендикулярная ей плоскость зеркального отражения порождают центр инверсии в точке их пересечения (рис. 10, в).

На рис. 10, г изображен случай, когда действуют одновременно все эти три правила.

В физической химии, в частности в молекулярной спектроскопии, для обозначения точечных групп применяется символика, введенная Шенфлисом. Точечные группы, содержащие операции только одной поворотной оси, обозначаются буквой С с индексом, показывающим порядок оси (например, С₃-группа, включающая только повороты на 120, 240, 360°). Точечные группы с единственной зеркально-поворотной осью n-го порядка обозначаются через S_n- Группы с дополнительными осями симметрии второго порядка, перпендикулярными главной оси, обозначаются буквой D с индексом, показывающим порядок главной оси. Наличие плоскости зеркального отражения, перпендикулярной главной оси, передается индексом h; а плоскостей, параллельных главной оси, - индексом v и т. д. Например, D₄ - группа с поворотной осью четвертого порядка и перпендикулярными ей осями второго порядка; C_4v - группа с поворотной осью четвертого порядка и параллельными ей плоскостями зеркального отражения; С_4v - группа стой же главной осью и перпендикулярной ей плоскостью зеркального отражения; D_4v - группа с поворотной осью четвертого порядка, перпендикулярными ей осями второго порядка и перпендикулярной ей плоскостью зеркального отражения (и, как следствие, с плоскостями отражения, параллельными главной оси, и центром инверсии в общей точке пересечения остальных элементов симметрии).

В структурной кристаллографии принята совсем иная система обозначения точечных групп, основанная на приведенных выше обозначениях элементов симметрии. Точечные группы, содержащие операции только одной поворотной оси, обозначаются, как и сами элементы симметрии, цифрами 1, 2, 3, 4,...; группы с единственной инверсионной осью - цифрами с черточками 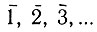.... Здесь 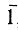-группа только с центром инверсии; 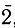- группа с единственной плоскостью симметрии; для нее предпочтительно обозначение m. Группы с осями симметрии второго порядка, перпендикулярными главной оси, обозначаются цифрами, стоящими подряд (например, 422 соответствует D₄). Добавление к главной оси плоскостей, ей параллельных, обозначается дополнением символа буквами m, стоящими подряд за цифрой (например, 4mm соответствует С_4v), а добавление плоскости, перпендикулярной главной оси, обозначается буквой m, стоящей за косой чертой (например, 4/m соответствует С_4h). Присутствие плоскостей симметрии как перпендикулярной оси, так и параллельных ей обозначается дополнением символа оси буквой m, стоящей за косой чертой, и буквами га, следующими вслед за ней (например, 4/mmm соответствует D_4h). Во всех случаях первая из букв, обозначающих плоскости, относится к плоскости, перпендикулярной главной оси.

Эта вторая система обозначений легко распространяется и на пространственные группы симметрии. Требуется лишь заменить (там, где это нужно) обозначение поворотных осей 2, 3, 4,... на обозначения винтовых осей 2₁, 3₁ (или 3₂), 4₁ (или 4₂, или 4₃) и т. д., а плоскостей зеркального отражения m на обозначения плоскостей скользящего отражения а, b, с, n или d. Более детально эта символика рассматривается в одном из последующих разделов.