§ 7. Взаимодействие трансляций и других операций симметрии

Хорошо известно, что требование групповой замкнутости операций симметрии приводит к определенным ограничениям в возможных комбинациях и взаимных ориентациях закрытых элементов симметрии конечных фигур. Это, в частности, было видно на только что рассмотренных примерах.

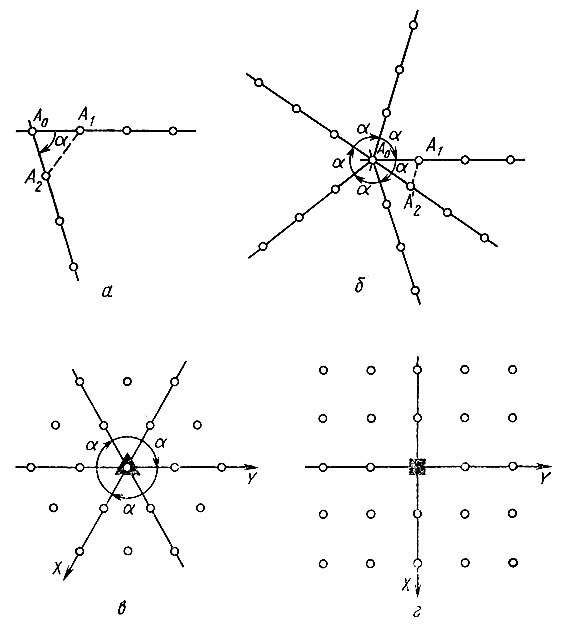
Рис. 11. К теореме о невозможности существования в кристалле осей пятого и выше шестого порядков

Те же ограничения действуют и по отношению к открытым элементам симметрии бесконечных фигур. Но помимо этого взаимодействие трансляций с другими операциями симметрии приводит к дополнительным ограничениям двух типов 1) трансляционная группа ограничивает возможный набор осей симметрии разных порядков; 2) любые операции симметрии, кроме простой инверсии, накладывают ограничения на геометрию (метрику) трансляционной группы.

Рассмотрим эти ограничения более подробно.

Возможные оси симметрии пространственной группы.

Поскольку трехмерная система переносов является обязательным свойством всякого кристалла, в кристалле возможны только такие (другие) элементы симметрии, которые не уничтожают его трансляционные свойства. Можно показать, что этим свойством обладают только оси 1, 2, 3, 4 и 6-го порядков. Это означает, что пространственных групп с осями пятого порядка или с любыми осями выше шестого порядка существовать не может. Сказанное, естественно, относится к поворотным, инверсионным и винтовым осям.

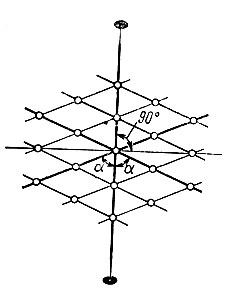
Рис. 12. Геометрия решетки кристалла в присутствии осей второго порядка

Теорема о невозможности существования в кристалле осей пятого и выше шестого порядков доказывается довольно просто.

Пусть два узловых ряда, пересекающихся в точке A₀ (рис. 11. а), определяются одним и тем же межузловым расстоянием, минимальным для узловой сетки, в которой лежат оба ряда (A₀A₁=A₀A₂=а_min). Тогда в треугольнике А₀А₁А₃ сторона А₁А₂ не может быть меньше, чем А₀А₁ (A₁A₂≥a_min), а следовательно, α≥60°. Это означает, что перпендикулярно сетке нельзя расположить ось симметрии выше шестого порядка. Сказанное относится и к инверсионным осям. Доказательство легко распространить и на винтовые оси.

Запрещенными оказываются и оси пятого порядка. Действительно, если повернуть исходный узловой ряд на угол 360/5=72° и учесть, что всякий узловой ряд бесконечен в обоих направлениях, то окажется, что "трижды повернутый" ряд образует с исходным угол в 36° (рис. 11, б), что приводит к соотношению А₁А₂<a_min Ось третьего порядка всем требованиям удовлетворяет (рис. 11, в). Не встречают возражений и оси 2-го, 4-го и 6-го порядков (на рис. 11, г приведена решетка с осями четвертого порядка).

Метрика решетки кристалла.

На рис. 12 показана ось 2 и проведен некий узловой ряд решетки, образующий с осью угол α. Поворотная симметрия требует существования эквивалентного ряда, повернутого относительно первого на 180°. Второй ряд образует с осью такой же угол α. Проведя все узловые ряды, параллельные первому и все узловые ряды, параллельные второму, мы легко убеждаемся, что в узловой сетке, построенной на этих двух рядах, должны также существовать ряды, перпендикулярные и параллельные оси симметрии. Этот результат - общий для любых осей симметрии, начиная с осей второго порядка.

Оси симметрии высших порядков, начиная с третьего, приводят к фиксации не только угловых, но и размерных параметров решетки. Действительно, самосовмещение фигуры при повороте на 120, 90 или 60° требует эквивалентности узловых рядов, повернутых относительно друг друга на указанный угол (см. рис. И). Эквивалентность означает равенство кратчайших трансляций в таких рядах.