§ 8. Классификационная схема пространственных групп симметрии

Из сказанного выше следует, что операции симметрии, возможные в кристаллическом пространстве, образуют друг с другом лишь строго определенные комбинации, число которых конечно. С другой стороны, такие комбинации достаточно разнообразны, поскольку в сочетаниях могут участвовать как закрытые, так и открытые операции симметрии.

Заслуга вывода всех возможных пространственных групп симметрии принадлежит акад. Е. С. Федорову. В 1890 г., задолго до первых работ по экспериментальному исследованию кристаллических структур, он по-казал, что существует всего 230 различных пространственных групп, и определил специфику каждой из них.

При столь большом наборе различных групп симметрии их естественно разбить на определенные семейства групп, родственных по тому или иному признаку. В качестве определяющего признака принято использовать либо порядок оси (безразлично какой - поворотной, инверсионной или винтовой), либо метрику трансляционной группы. Соответственно этому возникают два независимых потока классификационных подразделений, представленные ниже.

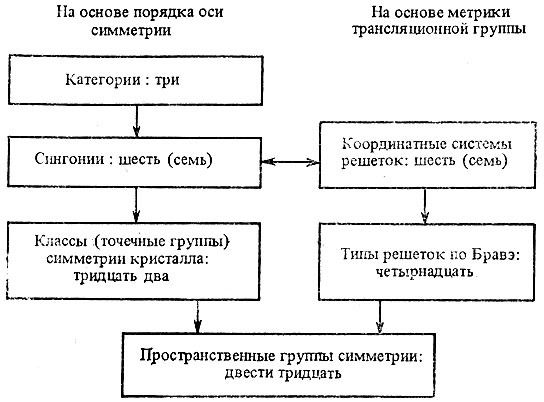
Сверху вниз идет детализация признаков. Если двигаться снизу вверх, можно сказать, что каждый класс симметрии объединяет некоторое число пространственных групп, каждая сингония - определенное число классов, каждая категория - определенное число сингоний. То же относится, в принципе, и к правому потоку. Двусторонняя стрелка между сингониями слева и координатными системами справа означает, что эти два понятия по содержанию очень близки, хотя и не полностью совпадают (см. ниже § 9 и 10).