§ 9. Классы симметрии, сингонии и категории

В теории симметрии кристаллического пространства существует понятие сходственных элементов симметрии. Таковыми являются поворотные и винтовые оси одного и того же порядка, плоскости зеркального и плоскости скользящего отражения. Понятие сходственности можно распространить и на группы симметрии: сходственны все пространственные группы, различающиеся лишь частичной или полной заменой закрытых элементов симметрии на сходственные им открытые элементы.

Если во всех сходственных пространственных группах произвести полную замену всех открытых элементов симметрии на закрытые и перенести их в общую точку пересечения, то получим одну и ту же точечную группу симметрии. Полученная таким преобразованием группа называется классом симметрии или точечной группой симметрии кристалла. Класс симметрии можно рассматривать как подразделение, объединяющее все сходственные пространственные группы.

Важность этого понятия связана с тем, что симметрия кристалла определяет и симметрию проявления самых разнообразных физических свойств. Но макрофизические свойства, такие, как электрическая проводимость, упругость и др., относятся не к отдельным атомам или атомным рядам, а к кристаллу в делом, и определяются не пространственной группой симметрии кристалла, а его классом симметрии - той точечной группой, которая получится, если все открытые элементы симметрии заменить сходственными закрытыми и перенести в общую точку пересечения.

Всего существует 32 класса симметрии. В левой части табл. 1 указаны их символы и количество пространственных групп, объединяемых в каждый класс симметрии.

Дальнейшие классификационные объединения точечных групп в более крупные семейства строятся по сугубо формальному признаку. Сингония кристалла определяется порядком и числом осей симметрии, присутствующих в точечной группе. Если в точечной группе имеется лишь поворотная или инверсионная ось первого порядка, то кристалл относят к триклинной сингонии^*. Если кроме осей первого порядка имеются только оси второго порядка, то точечные группы относятся либо к моноклинной, либо к ромбической сингонии. При этом моноклинная сингония объединяет классы с одной поворотной осью второго порядка, с одной инверсионной осью второго порядка или с одной поворотной и одной инверсионной осью при совпадении их по направлению^**. Ромбическая (или ортогональная^***) сингония объединяет те классы, в которых присутствует несколько осей симметрии второго порядка, разных по ориентации (взаимно перпендикулярных - в соответствии с правилами взаимодействия элементов симметрии). В том случае, когда в состав точечной группы входит одна ось симметрии четвертого порядка (безразлично, поворотная или инверсионная), группу относят к тетрагональной сингонии. Если в состав группы входит одна ось третьего или шестого порядка, то группа относится к гексагональной сингонии. В последней выделяют две подсингонии: тригональную (главная ось симметрии - ось третьего порядка) и собственно гексагональную (главная ось симметрии шестого порядка). Наконец, если в составе точечной группы имеется несколько осей высшего порядка (выше второго порядка), то такие группы относят к кубической сингонии. 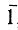и соответственно только две пространственные группы: в одной отсутствуют какие-либо элементы симметрии, кроме трансляционных осей, в другой - присутствуют только центры инверсии и трансляционные оси.

^* (Фактически сюда относятся только две точечные группы: полностью асимметричная 1 и центросимметричная )

^** (Поскольку инверсионная ось 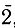адекватна перпендикулярной ей плоскости зеркального отражения, последний случай означает комбинацию из поворотной оси 2 и перпендикулярной ей плоскости m; равнодействующий элемент симметрии - центр инверсии 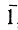в точке их пересечения.)

^*** (В западной литературе принят термин орторомбическая сингония.)

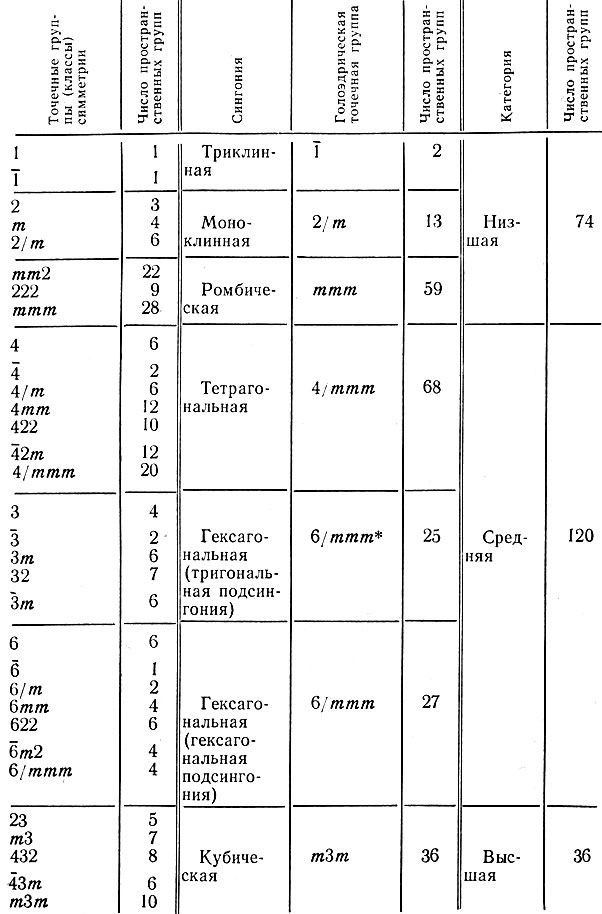
Таблица 1. Распределение пространственных групп по классам симметрии, сингониям и категориям

Распределение точечных групп по сингониям приведено в табл. 1. Все группы, относящиеся к одной и той же сингонии, являются подгруппами одной из них. В триклинной сингонии это группа 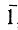, моноклинной 2/m, ромбической mmm, тетрагональной 4/mmm, гексагональной 6/mmm, кубической m3m. Такая группа высшей симметрии в данной сингонии называется голоэдрической.

В свою очередь сингонии объединяют в категории: низшую, среднюю и высшую. Здесь основным признаком является число осей высшего порядка. К низшей категории относят триклинную, моноклинную и ромбическую сингонию (осей высшего порядка нет). К средней - тетрагональную и гексагональную сингонию (оси высшего порядка ориентированы лишь в одном направлении пространства), к высшей - кубическую сингонию.