§ 11. Типы решеток Бравэ

Введение специальных правил выбора координатных осей в кристаллах каждой сингонии означает, естественно, отказ от первоначального постулата, гарантировавшего отсутствие узлов решетки внутри параллелепипеда, построенного на наименьших трансляциях, взятых за основные направления^*. Коль скоро координатные оси выбирают по направлениям осей симметрии, может случиться, что узлы решетки попадут и внутрь элементарной ячейки или на ее грани. Симметрия структуры (рис. 13) требует, чтобы оси X и Y были выбраны по двум взаимно перпендикулярным осям симметрии; это определяет прямоугольную форму грани ab элементарной ячейки. Между тем трансляционно равноценные фигуры располагаются в структуре не только в вершинах элементарных ячеек, но и в центрах их граней ab.

^* (Теперь это требование сохраняет силу только для групп, относящихся к триклинной сингонии.)

Если узлы решетки располагаются только в вершинах элементарных ячеек, то ячейку (и решетку в целом) называют примитивной. При наличии трансляций, совмещающих вершины ячеек с точками внутри или на гранях ячеек, решетка считается не примитивной (центрированной). В рассмотренном примере решетка центрирована в координатной плоскости XY (рис. 14, а).

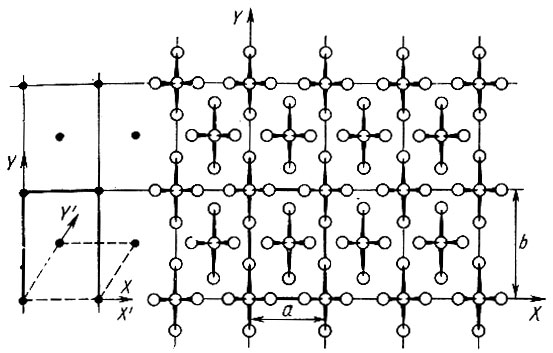
Рис. 13. Выбор координатных осей и элементарной ячейки в структуре с взаимно перпендикулярными плоскостями зеркального отражения

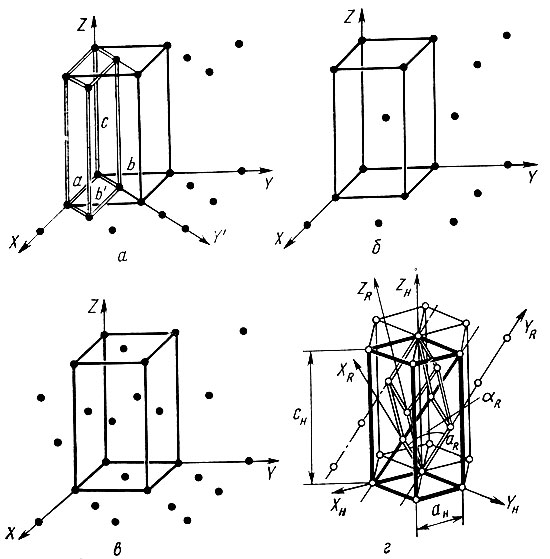
Рис. 14. Различные случаи центрировки решеток

Правила, определяющие выбор координатных систем в группах разных сингоний, по-разному ограничивают и способы центрировки их решеток. В триклинной сингонии в качестве осей можно выбрать любые некомпланарные узловые ряды, лишь бы объем получаемой ячейки был минимален. Поэтому триклинная решетка всегда примитивна. В моноклинной сингонии жестко зафиксировано направление лишь одной из осей, и в зависимости от размещения узлов решетки относительно этой оси она может оказаться либо примитивной, либо бокоцентрированной. В ромбической сингонии строго определены направления всех трех осей: решетка может быть как примитивной, так и базоцентрированной, объемно-центрированной или гранецентрированной (рис. 14, а, б, в). В группах тетрагональной сингонии оси X и Y всегда выбираются так, чтобы квадратное основание ячейки не содержало центрирующих узлов. Поэтому тетрагональная решетка может быть только примитивной или объемно-центрированной, но не базоцентрированной или гранецентрированной. В группах гексагональной сингонии, содержащих оси шестого порядка, возможна лишь примитивная (гексагональная) решетка, а в группах, содержащих оси только третьего порядка (тригональная подсингония), сверх того и ромбоэдрическая решетка (рис. 14, г). В кристаллах кубической сингонии разрешены примитивная, объемно- и гранецентрированные решетки. Как видно из этого перечисления, с учетом сингонии и способа центрировки возможно всего 14 различных типов решеток. Их называют решетками Бравэ.

В ромбоэдрической решетке за оси выбираются три узловых ряда, равнонаклонные к оси симметрии третьего порядка, создающие примитивную элементарную ячейку в форме ромбоэдра а=b=с и α=β=γ (рис. 14, г). Оси ромбоэдрической координатной системы обозначены на рисунке через X_R, Y_R, Z_R два независимых параметра решетки - через a_R и a_R. Но ту же решетку можно описать и в гексагональной системе координат (оси X_H, Y_H, Z_H, параметры решетки а_R, α_R) гексагональная элементарная ячейка в этом случае не примитивна, она содержит два узла на телесной диагонали на высотах 1/3 и 2/3 по Z. Поэтому ромбоэдрическую решетку часто называют и гексагональной дважды центрированной.

Для различных случаев центрировки ячеек применяются соответствующие обозначения: Р - примитивная решетка; А, В, С - решетки, центрированные по координатным плоскостям (YZ, XZ и XY соответственно); обычно их называют базо- или бокоцентрированными решетками; F - гранецентрированная решетка; I - объемно-центрированная решетка; R - ромбоэдрическая или дважды центрированная гексагональная решетка.

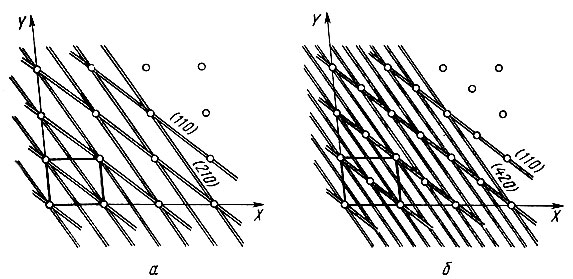
Рис. 15. Серии узловых сеток в примитивной (а) и центрированной (б) решетках

Эти обозначения применительно к решеткам разных сингоний приведены в табл. 2.

Индексы узловых сеток в не примитивных решетках

По определению, индексы узловых сеток h, k и l равны числу частей, на которые данная серия сеток разбивает ребра элементарной ячейки: а, b и с. Выше (см. §2) было показано, что в примитивной решетке целые числа h, k, l не могут иметь общего множителя. В не примитивных решетках дело обстоит иначе.

На рис. 15 изображены примитивная решетка и решетка, центрированная по плоскости XY (С-центрировка). Сетки (110) проходят одновременно и через узлы в вершинах ячеек, и через центрирующие узлы, поэтому они располагаются одинаково часто и в примитивной, и в С-решетке. Сетки (210), проведенные через Узлы в вершинах, не пересекают центрирующих узлов. В С-решетке возникают дополнительные "вставные" сетки, так что ребра ячейки а и b делятся уже не на 2 и 1 части, а на 4 и 2 части соответственно. По определению, индексы (210) здесь заменяются на (420).

Нетрудно проверить, что в данном примере индексы (hkl) любой серии сеток должны удовлетворять условию h+k=2n и не содержать других общих множителей.

Правила, фиксирующие значения индексов серий сеток в решетках разного типа, приведены во второй колонке табл. 3.^*

^* (Доказательство существования этих правил см., например, в кн.: Бокий Г. Б., Порай-Кошиц М. А. Рентгеноструктурный анализ Т.I. изд-во МГУ, 1964, с. 268-269)

Таблица 3. Индексы и серий узлов сеток и дифракционные индексы в решетках разного типа

^* (Других общих множителей нет.)

^** (Все три индекса четные или все три нечетные.)