§ 12. Графическое изображение пространственных групп симметрии

Совокупность элементов симметрии, образующих пространственную группу, их ориентацию и взаимное смещение в пространстве, удобнее всего показать графически в виде проекции на одну из граней элементарной ячейки трансляционной группы.

Понятно, что способ изображения каждого элемента симметрии зависит от того, располагается ли он перпендикулярно, параллельно или наклонно к плоскости проекции. На рис. 16 даны условные изображения осей симметрии разных порядков, как поворотных, так и инверсионных и винтовых: в верхнем ряду - оси, ориентированные перпендикулярно плоскости чертежа, в среднем - расположенные параллельно плоскости чертежа. В нижнем ряду приведены примеры изображения осей, наклоненных по отношению к плоскости проекции. Слева на рисунке (в виде маленького кружка) показано условное изображение центра инверсии.

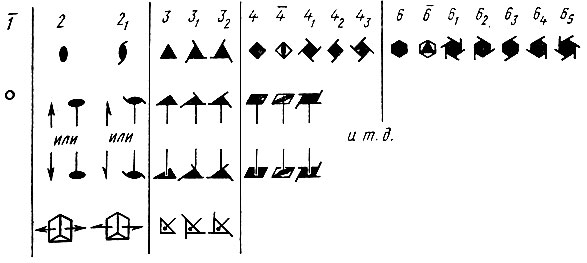
Рис. 16. Изображение осей симметрии на чертежах

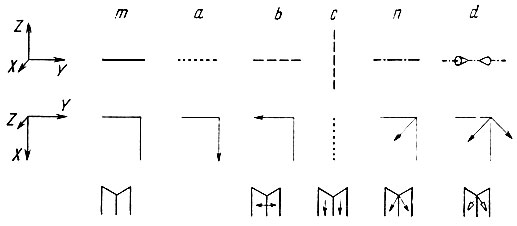
Рис. 17. Изображение плоскостей симметрии на чертежах

На рис. 17 аналогичным образом показано изображение плоскости зеркального и скользящего отражения. Плоскости, параллельные плоскости проекции (средний ряд на рисунке), изображаются в виде двух сходящихся, взаимно перпендикулярных прямых, помещаемых обычно в правом верхнем углу рисунка. Стрелка указывает направление скольжения. Отсутствие стрелки отличает плоскость зеркального отражения. В верхнем ряду те же плоскости ориентированы перпендикулярно плоскости чертежа: сплошная жирная линия означает зеркальное отражение; пунктирная - скользящее отражение со скольжением, перпендикулярным плоскости чертежа (на нас), штриховая - скольжение, параллельное плоскости чертежа: штрихпунктирная линия - диагональное n-скольжение. Дополнительные значки-стрелки на штрихпунктирной линии означают диагональное d-скольжение. В нижнем ряду приведены условные обозначения плоскостей симметрии, расположенных косо по отношению к плоскости чертежа.

Центры инверсии, а также плоскости и оси симметрии, параллельные плоскости чертежа, могут находиться в пространстве на разных уровнях над этой плоскостью. Величина смещения над плоскостью чертежа (над координатной плоскостью элементарной ячейки) обозначается дробным числом, которое ставится рядом с изображением элемента симметрии и означает величину смещения в долях периода повторяемости.

Обычно пространственную группу принято показывать в проекции на координатную плоскость XY. Ось X направляется в проекции сверху вниз, ось Y- слева направо; предполагается, что ось Z направлена на нас (правая система координат).

На рис. 18 в верхнем ряду в качестве простых примеров приведены изображения двух пространственных групп моноклинной сингонии.

Чертежи нетрудно "прочесть". В левой части рисунка изображена группа с поворотными осями второго по-рядка, параллельными оси Y, плоскостями зеркального отражения, перпендикулярными этой оси. В точках их пересечения находятся центры инверсии. В правой части рисунка показана группа с винтовыми осями второго порядка, параллельными оси Y, и плоскостями скользящего отражения, им перпендикулярными, со скольжением вдоль оси Z.

Центры инверсии размещаются (так же, как в первой из показанных групп) в начале координат и в точках 1/2 00,0 ? 0, 1/2 1/2 0, 00 1/2, 0 1/2 1/2, 1/2 0 1/2 и 1/2 1/2 1/2 . Винтовые оси смещены относительно центров инверсии на 1/4 периода по оси с, а плоскости скольжения - на 1/4 периода по оси Y.

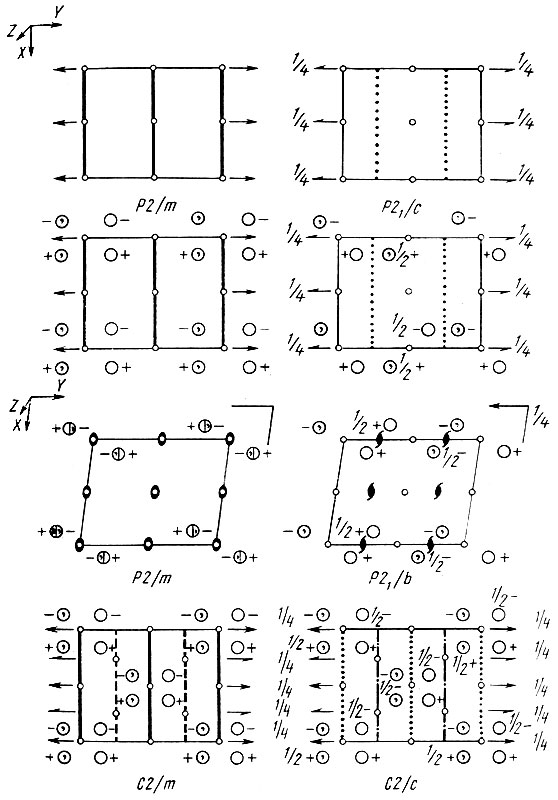
Рис. 18. Изображение некоторых пространственных групп моноклинной сингонии

При изображении пространственных групп принято показывать на чертежах не только сами элементы симметрии, но и размножаемые ими материальные частицы. Последние изображаются кружками. Знаки + и - около них указывают, где (над или под плоскостью чертежа) располагаются точки (подразумеваются координаты +z и -z, если на нас направлена ось Z ячейки). Если кружок разделен пополам чертой и около него стоят оба знака, это означает присутствие двух точек - и над, и под плоскостью чертежа. Замена знаков + и - на 1/2+ и 1/2- означает перенос точки, имевшей координату z, перпендикулярно плоскости чертежа в точку с координатой 1/2+z или 1/2-z по той же оси. Точки (материальные частицы), которые переводятся друг в друга инверсией или отражением, в принципе не конгруэнтны, а лишь зеркально равны. Для того чтобы отразить это обстоятельство, одна из двух таких точек снабжается пометкой в виде запятой.

Во втором ряду на том же рисунке повторены обе показанные в верхнем ряду пространственные группы, дополненные изображением материальных точек. Нетрудно проверить, что присутствующие элементы симметрии действительно переводят эти точки друг в друга: по обе стороны от поворотной оси 2 располагаются кружки с разными знаками + и -, но одинаковой пометкой; по обе стороны от плоскости m располагаются кружки с одинаковыми знаками (оба + или оба -), но с разными пометками (один без запятой, второй с запятой); по обе стороны от центра инверсии располагаются кружки с разными знаками и разными пометками. На правом рисунке плоскость скользящего отражения со скольжением вдоль Z-оси связывает кружки со знаками + и 1/2+ или - и 1/2- (имеются в виду координаты z и 1/2+z). Винтовая ось, поднятая на уровень 1/4 по Z, связывает точки с координатами xyz и х, 1/2+y, 1/2-z.

В табл. 2 указывалось, что для пространственных групп моноклинной сингонии общеприняты не одна, а две различные установки: одна с осью симметрии по оси Y кристалла, другая с осью симметрии по оси Z кристалла. На чертежах, приведенных в верхней части рис. 18, использована Z-установка: поворотная ось 2 на левом чертеже и винтовая 2₁ на правом направлены вдоль оси Y.

В третьем ряду те же две пространственные группы даны в Z-установке; оси симметрии 2 и 2₁ проходят параллельно оси Z-кристалла. На рисунках представлены проекции ячеек на координатную плоскость XY, но в этой установке оси симметрии располагаются уже не параллельно, а перпендикулярно плоскости чертежа. Соответственно изменяется и ориентация плоскостной симметрии.

Наличие плоскости зеркального отражения, параллельной плоскости чертежа, приводит к появлению материальных точек, накладывающихся друг на друга в проекции; кружки разделены пополам и снабжены обоими знаками + и -.

В последнем ряду показаны две другие пространственные группы, тоже относящиеся к моноклинной сингонии. Здесь снова принята Y-установка. Не анализируя всех особенностей размещения элементов симметрии, обратим внимание лишь на следующее. В обоих случаях весь комплекс кружков, расположенных вокруг вершин элементарной ячейки (вместе со знаками + и - и пометками-запятыми), переносится как целое в центр проекции. Это означает, что в решетке имеется трансляция, равная половине длины диагонали основания ячейки. Обе группы в отличие от двух предшествующих имеют не примитивную, а базоцентрированную трансляционную подгруппу.