Интерференционное уравнение

Условие Лауэ и уравнение Брэгга, имея алгебраическую форму, по сути выражают связь между геометрическими параметрами - направлениями первичного пучка, дифракционного луча, ориентацией кристалла и его параметрами. Естественно поэтому перейти к векторному выражению этой взаимосвязи.

Пусть серия плоскостей (hkl) с межплоскостным расстоянием d_hki находится в отражающем положении. Зададим направление первичного пучка единичным вектором S₀, направление дифракционного луча - единичным вектором S (рис. 29, а). Составим векторную разность S-S₀.

Поскольку угол падения равен углу отражения, вектор S-S₀ направлен перпендикулярно отражающей серии плоскостей, а поскольку |S|=|S₀|=1, по длине он равен 2sinθ;. Следовательно, S-S₀=2sinθN_hkl, где N_hkl - единичный вектор, нормальный к плоскостям (_hkl).

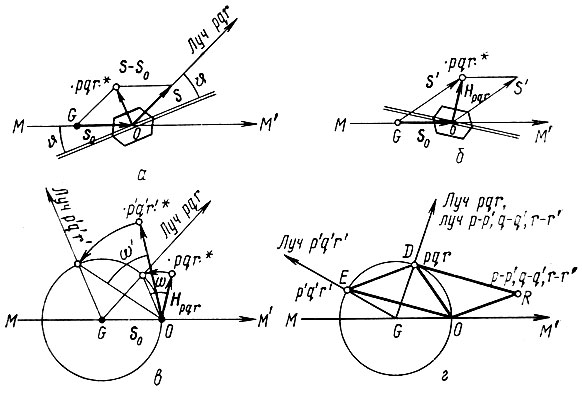
Рис. 29. К выводу и интерпретации интерференционного уравнения: а - кристалл находится в отражающем положении для дифракции pqr; б - кристалл не находится в отражающем положении; в - поворот кристалла на угол θ) в отражающее положение; г - случай одновременных отражений

По уравнению Брэгга 2sinθ=X(n/d_nkl). Это означает, что S-S₀=λ(n/d_hkl)N_hkl.

Введем обратную решетку кристалла с масштабным коэффициентом М, равным λ. Величина, стоящая в правой части, согласно (11), представляет собой вектор обратной решетки, проведенный в узел с индексами ·pqr· (т. е. ·nh, nk, nl·). Следовательно,

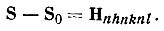(21)

Полученное соотношение называется интерференционным уравнением. Оно определяет в явной форме взаимосвязь между направлением дифракционного луча S и ориентацией серии плоскостей (hkl) в момент получения отражения n-го порядка; эта ориентация задается соответствующим вектором обратной решетки H_nhnkm^*. Перепишем интерференционное уравнение в форме

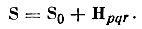
Оно, собственно, означает следующее: кристалл находится в ориентации, отвечающей появлению дифракционного луча pqr в том случае, если векторная сумма единичного вектора первичного пучка S₀ и вектора обратной решетки H_pqr дает вектор единичной длины.

^* (Интерференционное уравнение позволяет также наглядно проследить связь между лауэвским и брэгговским представлением дифракционного эффекта. Если обе части векторного равенства взять по абсолютной величине, то приходим снова к уравнению Брэгга; если же обе части умножить на а, b и с последовательно, то получим три условия Лауэ. Например, )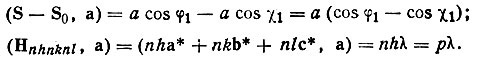

На рис. 29, б показан случай, когда это условие не удовлетворяется: вектор S', равный сумме S₀+H_pqr, по длине явно больше единицы (больше, чем |S₀|); кристалл не находится в отражающем положении. Что нужно сделать, чтобы возник луч pqr? Ответ на этот вопрос дает рис. 29, в. Вокруг точки G (исходной точки вектора S₀) проведена сфера единичного радиуса. Узел обратной решетки pqr не находится на поверхности этой сферы. Но если кристалл, а следовательно, и его обратную решетку повернуть против часовой стрелки на некоторый угол со, то этот узел окажется на поверхности сферы, и векторная сумма S₀+H_pdr=S по абсолютному значению будет равна единице. При этой ориентации и возникает дифракционный луч pqr^*.

^* (Отметим попутно одну особенность рис. 29, в. Дифракционный луч теперь исходит не из точки О, а из точки G. Но это несущественно, поскольку сказанное относится к любому дифракционному лучу. По существу, мы лишь разнесли по разным точкам кристалл (перенесли его в точку G) и начало координат обратной решетки (точка О). )

Для каждого дифракционного луча нужна своя ориентация кристалла. На том же рисунке 29, в показан и другой узел обратной решетки p'q'r' и соответственно вектор Н_p'q'r. Для получения дифракционного луча p'q'r' этот вектор (т. е. кристалл) нужно повернуть на иной угол ω', и направление этого дифракционного луча будет, естественно, уже иным.

Вспомогательную сферу, позволяющую найти ориентацию кристалла в отражающем положении для любого луча pqr, называют сферой отражения.

Возможны такие случаи, когда на поверхность сферы отражения попадают одновременно два узла обратной решетки. Это означает, что помимо измеряемого детектором дифракционного луча pqr одновременно (в другом направлении) возникает второй дифракционный луч p'q'r'. Это приводит к изменению амплитуды, а следовательно, и интенсивности измеряемого отражения pqr, причем она может оказаться как пониженной, так и повышенной.

Остановимся на этом несколько подробнее. На рис. 29, г точка D-узел pqr на поверхности сферы отражения, точка E-узел p'q'r', также попавший на поверхность сферы отражения при той же ориентации кристалла. Так как мы имеем дело с обратной решеткой, в ней должен быть и узел с индексами р-р', q-q', r-r', расположенный (в момент отражения pqr) в точке R.

Если второй дифракционный луч p'q'r' достаточно интенсивный, то он может создать заметный вторичный дифракционный эффект. Чтобы учесть результаты этого эффекта, нужно принять луч ОЕ за первичный, т. е. перенести начало координат об-ратной решетки в точку Е без изменения ориентации решетки. Точка О совместится с точкой Е, а точка R с точкой D и, следовательно, в направлении GD должен возникнуть не только дифракционный луч pqr, но и вторичный (от луча p'q'r') дифракционный луч р-р', q-q', r-r'. Лучи pqr и р-р', q-q', r-r' имеют разную начальную фазу, и в зависимости от сдвига по фазе второй из них может как усилить, так и ослабить луч pqr.

О возможности таких одновременных отражений следует всегда помнить. В современных дифрактометрах (см. ниже) предусматривается возможность избавиться от таких отражений. Ведь для этого необходимо лишь повернуть кристалл на небольшой угол вокруг вектора OD (нормального к серии отражающих плоскостей). При таком повороте узел Е сдвинется с поверхности сферы отражения (на рис. 29, г "к нам" или "от нас") и луч p'q'r' перестанет существовать.

Интерференционное уравнение вкладывает новое, более глубокое содержание в понятие обратной решетки. Теперь каждый узел ее однозначно связан с определенным дифракционным лучом pqr и может рассматриваться как некое условное изображение этого луча. И наоборот, рентгенограмму, полученную методом вращения или одним из рентгенгониометрических методов, можно считать искаженным изображением (проекцией) определенной части обратной решетки. Способ "искажения" зависит от кинематической схемы каждого из рентгенгониометрических методов. Но коль скоро она известна, переход от рентгенограммы к обратной решетке не представляет труда. А поскольку порядок обозначения узлов в решетке известен, такой переход дает наиболее простую и удобную основу для определения дифракционных индексов (индицирования) рентгенограмм.

Справедливо и обратное. По заданным индексам pqr, а следовательно, и по вектору H_pqr достаточно легко определить и угол со поворота кристалла из исходного положения в отражающее и направляющие углы дифракционного луча, т. е. найти ориентацию кристалла и положение счетчика в дифрактометре для регистрации дифракционного луча pqr.

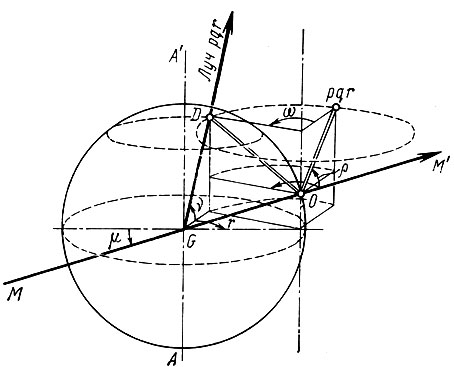
Рис. 30. Общий случай поворота кристалла в отражающее положение

Поскольку далее будут рассмотрены кинематические схемы некоторых наиболее распространенных монокристальных дифрактометров, следует несколько детальнее остановиться на понятии направляющих углов дифракционного луча.

Рис. 29, в в сущности описывает простейший случай, когда ось вращения направлена перпендикулярно пучку ММ' (направлена на нас) и рассматривается вектор Н_pqr (и H_p'g'r'), лежащий в плоскости, перпендикулярной оси вращения (в плоскости чертежа).

На рис. 30 представлен (в иной проекции) более общий случай. Ось вращения АA' кристалла лежит в плоскости чертежа, а первичный пучок ММ', также лежащий в плоскости чертежа, направлен наклонно к оси вращения и образует угол μ с плоскостью, ей перпендикулярной. Выбранный вектор H_pqr образует с той же плоскостью угол р.

При вращении кристалла вектор H_pqr описывает конус, и при повороте на угол ω пересекает сферу отражения не в ее экваториальной плоскости, а в точке D кругового сечения, расположенного выше экваториальной плоскости. Соответственно дифракционный луч pqr, идущий из центра сферы отражения через точку пересечения D направлен наклонно к оси вращения. Его направление удобно характеризовать двумя углами: углом Υ в его проекции на экваториальную плоскость и углом v отклонения от экваториальной плоскости.

Понятно, что углы р, μ и Υ взаимосвязаны. Эту взаимосвязь нетрудно передать в математической форме. В частности, можно показать, что

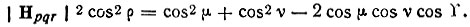
Естественно, что в это соотношение вошла и длина вектора обратной решетки, т. е. параметры решетки кристалла а, b, с, α, β, γ и индексы дифракционного луча pqr.

Угол ω независим от остальных углов, поскольку он характеризует угол поворота кристалла из некоторого начального (произвольного) положения в отражающее.