§ 2. Структурная амплитуда и координаты атомов

Если в некотором направлении распространяется несколько независимых волн одной и той же периодичности, но различных по своим амплитудам Е_j, и начальным фазам δ_j, то в результате их интерференции возникает волна той же периодичности. Формула, позволяющая определить амплитуду и начальную фазу результирующей волны (Е_pез и δ_рез), хорошо известна из оптики, теории переменных токов и других дисциплин, имеющих дело с волнами:

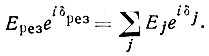(23)

Комбинацию Еe^{i δ} часто называют комплексной амплитудой. Следовательно, общий закон интерференции можно сформулировать так: комплексная амплитуда результирующей волны равна сумме комплексных амплитуд налагающихся волн.

Применим формулу (23) к дифракционному лучу. Суммарная волна дифракционного луча слагается из волн, рассеянных каждой из элементарных ячеек кристалла, а последние, в свою очередь, из волн, рассеянных отдельными атомами ячейки. Волны, рассеиваемые в дифракционном направлении разными элементарными ячейками, согласно определению совпадают по фазе, поэтому

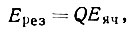(24)

где Q - число ячеек в кристалле.

Атомы расположены в разных точках ячейки, и волны, рассеиваемые ими, не совпадают по фазе (не различаются по фазе на целое число периодов). В этом случае надо учесть различие как в рассеивающей способности атомов f_j, так и в их начальных фазах δ_j:

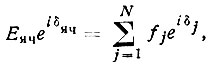(25)

где N - общее число атомов в элементарной ячейке.

Требуется лишь уточнить значения δ_j и f_j каждого атома.

1. Начальные фазы волн, рассеиваемых атомами, зависят от координат атомов. На рис. 38 представлена элементарная ячейка некоторого кристалла. В начале координат ячейки может и не быть никакого атома, однако луч, проведенный из М в N через начало координат O, служит основой для отсчета начальных фаз. Путь луча от М к N через некоторый j-й атом меньше пути этого реперного луча на величину OB-СА или в векторной форме на Sr_j-S₀r_j=(S-S₀, r_j), где S и S₀- единичные векторы. Составив пропорцию (ОВ-CA)λ= δ_j/2π, получим для начальной фазы
   
   
   Или, в соответствии с интерференционным уравнением (21),
   (26)
   
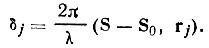   Далее представим Н_hkl в виде
   
   
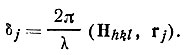   по (2) в виде x_ja+y_jb+z_jc, где x_j, y_j,z_j - относительные координаты j-го атома. Учитывая, что масштабный множитель перехода от прямой к обратной решетке в интерференционном уравнении равен λ,, получим окончательно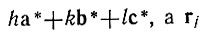
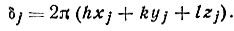   (27)
   
   
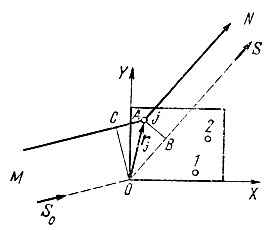
   Рис. 38. Смещение по фазе волн, рассеянных разными атомами ячейки в дифракционном направлении
   
   
2. Рассеивающая способность атома f_j зависит от его атомного номера, длины волны лучей λ и угла рассеяния φ. Характер этой зависимости показан на рис. 39. Постепенное уменьшение амплитуды с увеличением угла φ (равного 2 θ) вызывается тем, что рентгеновские лучи рассеиваются электронным облаком атома, распределенным по пространству. Расхождение по фазе волн, рассеянных разными участками электронного облака, возрастает с увеличением угла φ, что и приводит к снижению суммарной амплитуды. Это снижение происходит тем резче, чем меньше длина волны λ. При более строгом рассмотрении можно показать, что единым аргументом зависимости f от φ и λ может служить sinθ/λ.

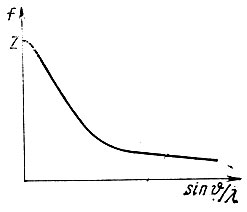
Рис. 39. Зависимость рассеивающей способности атомов f от угла θ и длины волны λ

Зависимость f от sin θ/λ называется функцией атомного рассеяния. Эта зависимость известна для всех элементов с достаточной точностью и приводится в соответствующих справочниках. Отметим лишь, что амплитуду рассеяния атомом f принято выражать в так называемых электронных единицах.

За единицу принимается амплитуда рассеяния одним электроном в том же направлении. Величина f показывает, во сколько раз амплитуда рассеяния атомом больше, чем электроном. В электронных единицах, следовательно, выражается и амплитуда рассеяния кристаллом в целом^*.

^* (Кривая атомного рассеяния, представленная на рис. 39, не учитывает тепловых колебаний атомов. Такие колебания дополнительно размазывают электронную плотность атома, что должно отразиться на кривой атомного рассеяния - увеличить скорость падения значения f с увеличением sin θ/λ. Следовательно, строго говоря, мы должны иметь дело с произведением fτ, где τ - поправка на тепловые колебания атомов, так называемый температурный фактор. Однако на начальной стадии расшифровки структуры этой поправкой можно пренебречь. К формуле, характеризующей температурный фактор, мы вернемся при обсуждении методов уточнения структуры (§ 10 этой главы).)

Подставив табличные значения атомных амплитуд fj и выраженные по (27) значения δ_j в формулу (25), получим комплексную величину

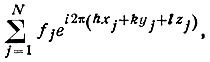
которую принято называть структурной амплитудой. Модуль этой комплексной величины представляет собой амплитуду суммарного дифракционного луча, выраженную в электронных единицах и рассчитанную на одну элементарную ячейку, а ее аргумент - начальную фазу суммарного дифракционного луча. Обозначается структурная амплитуда как F|hkl| или в развернутом виде |F (hkl)|e^iφ(hkl) где |F(hkl)|-амплитуда, φ (hkl) - начальная фаза дифракционного луча . Окончательная формула структурной амплитуды имеет следующий вид:

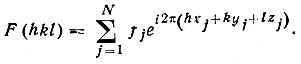(28)

Это первая из двух основных формул структурного анализа; она выражает зависимость амплитуды и начальной фазы любого дифракционного луча от координат атомов в структуре и позволяет решать задачу, обратную поставленной перед исследователем: по известным координатам определять интенсивность дифракционных лучей. В сущности именно этой формулой (и только ею) приходилось пользоваться при анализе структуры методом проб и ошибок в первый период существования структурного анализа. Модель гипотетической структуры (координаты атомов) выводилась из косвенных соображений и проверялась соответствию значений формуле (28), экспериментальным значениям интенсивности |F (hkl)| ² I(hkl)_эксп.

Рис. 40. К выводу зависимости начальной фазы луча, рассеянного атомом в дифракционном направлении от координат атома [взята серия плоскостей (230)]

^* (Во избежание недоразумений подчеркнем смысловое различие между δ_j и φ(hkl); ξ_j - начальная фаза луча, рассеянного в дифракционном направлении атомами j-го сорта; φ(hkl)-начальная фаза суммарного дифракционного луча hkl. )

Читателю, решившему опустить раздел, в котором вводится представление об обратной решетке (гл. I, § 3), можно предложить несколько иной вариант вывода соотношения (27).

На рис. 40 изображена элементарная ячейка и проведена ближайшая к началу координат узловая сетка серии плоскостей h₀k₀l₀. Отмечен j-й атом ячейки; через него проведена плоскость АВ, параллельная узловой сетке. Межплоскостное расстояние узловых сеток равно d_hkl ; расстояние плоскости АВ от сетки, проходящей через начало координат, равно Разность фаз лучей, отраженных (в n-м порядке) от двух соседних узловых сеток, составляет 2πп, а лучей, отраженных плоскостью АВ δ и сеткой, проходящей через начало координат, δ. Отсюда вытекает

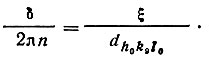(29)

Рассматриваемый j-й атом с координатами x_j, y_j, z_j лежит в плоскости АВ. Следовательно, начальная фаза лучей, рассеянных этим атомом в дифракционном направлении hkl (с h=nh₀, k= nk₀, l=nl₀), равна той же величине δ:

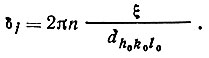(30)

Остается найти отношение ξ/d h₀k₀l₀- Для этого воспользуемся уравнением плоскости АВ (уравнение плоскости в отрезках):

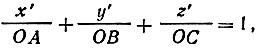(31)

где ОА, ОВ, ОС - отрезки, отсекаемые плоскостью на координатных осях, х', у, z' - абсолютные (в Å) координаты любой точки плоскости АВ. Но из подобия треугольников на рис. 40 (или, точнее, из подобия пирамид в трехмерном пространстве) следует, что эти отрезки пропорциональны отрезкам, отсекаемым на тех же осях плоскостью (h₀, k₀, l₀), т. е. величинам a/h₀, b/k₀ и c/l_0> соответственно:

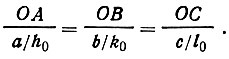
С другой стороны, каждое из этих отношений должно быть равно и отношению высот двух треугольников (пирамид), т. е. ξ/d_h0k0l0. Следовательно,

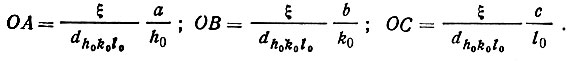
Подставляя эти выражения в (31), получаем

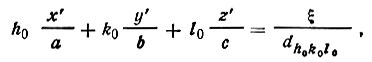
где х', у', z' - координаты любой точки плоскости АВ, в том числе координаты j-го атома x'_jy'jz'j.

Перейдем к относительным координатам х_j=х'_j/а, y_j= y'_j/b, z_j=z'_j/c и учтем, что nh₀=h, nk₀=k, nl₀=l, где hkl - индексы рассматриваемого дифракционного луча. Получим n ξ/d_h0k0l0= hx_j+ky_j+lz_j- Подставляя это соотношение в (30), приходим к формуле (27):

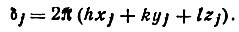
Отметим еще следующее. Структурная амплитуда отражения с индексами 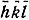дается формулой

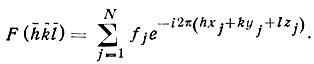
Следовательно, F( 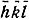)=F* (hkl), где F* (hkl) обозначает величину, комплексно-сопряженную по отношению к F(hkl). Иначе говоря,

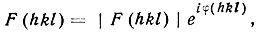(32)

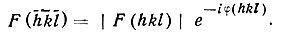
Дифракционные лучи hkl и 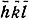имеют одинаковые амплитуды и противоположные фазы. Поскольку I∼|F|², оба луча имеют одинаковую интенсивность. В этом и заключается одно из двух положений, содержащихся в законе Фриделя о центросимметричности рентгеновской оптики.

Как уже отмечалось, закон Фриделя нарушается, если рентгеновские лучи попадают в область аномального рассеяния атома одного из (или ряда) элементов, входящих в состав кристалл Эта область определяется близостью длины волны рентгеновских лучей к краю К- или L-полосы их поглощения элементом; если λ края полосы поглощения элементом несколько больше, чем λ чей, то рассеяние лучей атомами этого элемента сопровождается небольшим изменением их начальной фазы. Этот дополнительный сдвиг по фазе отражается, естественно, и на результирующей амплитуде дифракционного луча.

Практически он учитывается заменой табличного значения атомной амплитуды атома f⁰_j на комплексную величину f_j=f⁰_jeⁱφ_j где φ_j - сдвиг по фазе, вызванный аномальным рассеянием. Поскольку φ_j- мало, более удобна формула f_j = (f⁰_j+Δf')+iΔf"_j, где Δf_j и Δf"_j - малые по величине поправки к исходной амплитуде f⁰_j. Как и f_j, эти поправки приводятся в специальных справочниках в виде таблиц в функции λ и Z_j.

Комплексные f_j заменяют вещественные f⁰j в формуле структурной амплитуды (28). Так как сдвиг по фазе φ_j не зависит от индексов дифракционного луча и, в частности, не заменяется на обратную величину при переходе от hkl к 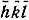, то включение поправки на аномальное рассеяние делает лучи с индексами hkl и 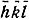не вполне равноценными по интенсивности и, следовательно, нарушает закон центросимметричности рентгеновской оптики.