§ 3. Структурные амплитуды и распределение электронной плотности по ячейке

Электронная плотность любого атома распределена определенным образом по пространству. В формуле структурной амплитуды подразумевалось, что результат рассеяния лучей различными точками каждого атома, взятого в отдельности, уже известен; он и дается в виде значений f(sin θ/λ). Можно, однако, поступить и иначе: рассматривать элементарную ячейку кристалла как непрерывное распределение электронной плотности с максимумами-сгустками в центрах тяжести разных атомов. При таком подходе суммирование в формуле (28) следует заменить на интегрирование по ячейке, a f_j на амплитуду рассеяния электронной плотностью в бесконечно малом объеме dV. И так как амплитуда выражается в электронных единицах, ее величина равна просто p(xyz)dV, где р(xyz)-электронная плотность в точке xyz. В результате получим

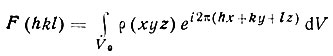(33)

(интегрирование по объему элементарной ячейки V₀). Выражение (28) можно назвать алгебраической, а (33)-интегральной формой записи структурной амплитуды.

Формулы типа (33) обращаются с помощью преобразования Фурье. Если, например,

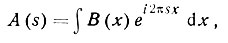
то

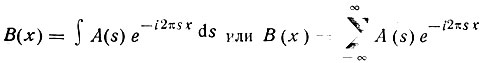(34)

если В(х) -периодическая функция.

В данном случае речь о трехмерной периодической функции: распределение электронной плотности повторяется в каждой ячейке во всех трех измерениях. Поэтому преобразование Фурье здесь имеет вид тройного ряда Фурье:

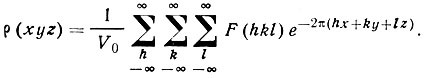(35)

Уравнение (35)-вторая основная формула структурного анализа. Она выражает зависимость электронной плотности в некоторой точке ячейки от совокупности структурных амплитуд лучей, дифрагированных кристаллом. Если известны структурные амплитуды всех отражений, то можно найти значение p(xyz) в любой точке, а значит, и распределение плотности по ячейке, в том числе и положение всех максимумов - центров тяжести электронных облаков атомов.

Структурные амплитуды линейно связаны с атомными амплитудами [формула (28)], а последние убывают по мере увеличения sin θ/ λ, а следовательно, и по мере увеличения индексов hkl. Поэтому сами F(hkl), разные для разных отражений, в среднем также уменьшаются по величине по мере возрастания индексов. Это позволяет оборвать ряд Фурье на некоторых максимальных индексах без внесения существенных ошибок в результатах.