§ 4. Учет симметрии в формулах структурной амплитуды и электронной плотности

В формуле (28) суммирование охватывает все атомы элементарной ячейки, как симметрически независимые, так и связанные между собой операциями симметрии пространственной группы кристалла.

Разделив атомы по этому последнему признаку, можно переписать формулу (28) в виде

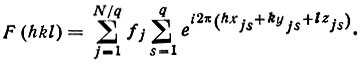(36)

Внутреннее суммирование (no s) охватывает атомы ячейки, связанные между собой операциями симметрии. Эта сумма может быть преобразована в более удобную форму заранее безотносительно к конкретным координатам атомов. Например, в пространственной группе Рmm2 (примитивная решетка с осью второго порядка вдоль оси Z и двумя плоскостями зеркального отражения по XZ и YZ, рис. 41) симметрически связаны четверки атомов с координатами xyz,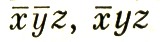 и xȳz; внутреннее суммирование дает

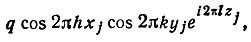(37)

где q=4, если атомы занимают общую четырехкратную позицию; q=2, если они расположены на плоскостях зеркального отражения и q=1 при расположении атома на двойной оси.

Одновременно симметрия сокращает число отражений, для которых приходится производить расчеты, так как она уравнивает значения структурных амплитуд с одинаковыми по модулю и разными по знаку индексами. Так, из (37) следует, что в рассмотренном примере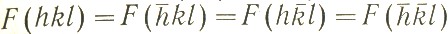

Вызываемое симметрией выравнивание структурных амплитуд позволяет, в свою очередь, преобразовать формулу электронной плотности: сократить пределы суммирования, учтя заранее симметрически связанные F(hkl). В рассматриваемом примере

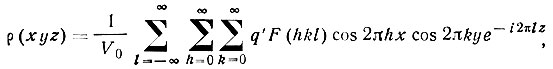(38)

где q'=4, если h≠0 и q'=2, если h или k = 0 и q'= 1, если h=0 и k=0.

Само собой разумеется, что расчет электронной плотности производится только для симметрически независимой части элементарной ячейки. В случае Рmm2 таковой является 1/4 ячейки, заключенная в области от 0 до 1/2 по x и по y от 0 до 1 по z.

Преобразованные формулы F (hkl) и р (xyz) и правила взаимосвязи между F(hkl) приводятся в специальном справочнике "Международные таблицы для определения кристаллических структур"^*.

^* (International Tables for Crystsllogarhy. Blrmingam: Kynoch Press, 1052-1962 V. I, II, III )

В табл. 3 (гл. I, § 11) были приведены без доказательства правила, характеризующие численные значения индексов серий угловых сеток в центрированных решетках. На этой основе (при умножении индексов сеток на порядок отражения n) были получены правила погасаний дифракционных индексов для не примитивных решеток. Теперь, используя формулу структурной амплитуды, можно вывести эти правила погасаний из законов расположения атомов в центрированных решетках, а следовательно, действуя в обратном направлении, - и правила, характеризующие индексы узловых сеток.

Возьмем, например, решетку, центрированную по грани XY. Это означает, что все атомы ячейки связаны попарно соотношением x_j, у_j, z_j и x_j +1/2, y_j +1/2, z_j. Подставим это соотношение в формулу (36):

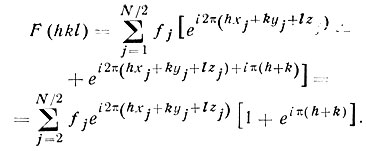
Если h + k = 2n, то 1+e^iπ(h+k)= 2, если h + k=2n-1, то 1+e^iπ(h+k)=0 Следовательно, все отражения hkl с h+k нечетными имеют нулевую интенсивность, "погашены".

Аналогичным образом можно проверить и все другие правила погасаний, приведенные в табл. 3.

Можно установить и правила погасаний, вызываемых плоскостями скользящего отражения и винтовыми осями. Предположим, например, что плоскость n (диагонального скольжения) проходит по координатной плоскости XY. Атомы ячейки связаны попарно соотношением x_j, y_j, z_j и x_j+1/2, x_j+1/2, y_j+1/2, z_j Формула (36) тогда примет вид

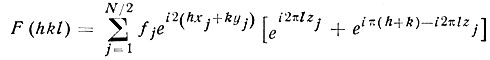
или

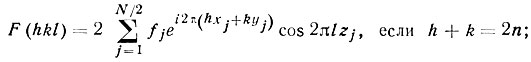
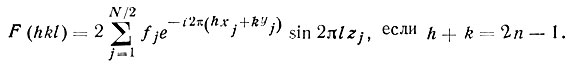
В общем случае отражений hkl с ненулевым l F(hkl) отлично от нуля независимо от четности или нечетности индексов. Но для отражений типа hk0 дело обстоит иначе: cos0=1, a sin 0=0, и все отражения hk0 с h + k = 2n-1 оказываются погашенными.

Допустим теперь, что по оси Z кристалла проходит винтовая ось 4₁ В ячейке присутствуют четверки атомов x_j, у_j, z_j; ȳ_j, x_j, z_j+1/4; x_j, y_j, z_l+1/2; y_j, x_j, z_j+3/4. Эти соотношения таковы, что ожидать погасаний среди отражений hkl с ненулевыми индексами или с одним нулевым индексом не приходится. Возьмем, однако, лишь отражения 00l. Здесь

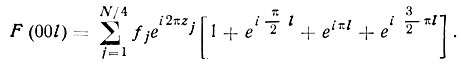
При любых l, кроме кратных четырем, в квадратных скобках чередуются + 1, -1 и i, -i. При l = 4п все четыре слагаемых равны + 1 и F(00l)≠0.