Взаимосвязь между структурными амплитудами. Равенство Сейра

Фазовое соотношение между тройками сильных отражений Φ⁽³⁾≅0 можно вывести более строго на основе второго требования к распределению электронной плотности - наличия в нем максимумов, отвечающих отдельным атомам и вытекающего из этого требования равенства Сейра.

В структуре, состоящей из одинаковых атомов,

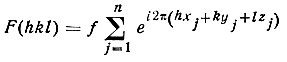
[см. формулу (28)]. Рассмотрим гипотетическую структуру с электронной плотностью р²(r) вместо р(r) во всех ее точках ("квадратичная" структура). Ее "атомы" находятся в тех же позициях, что и в исходной структуре, но обладают уже иной рассеивающей способностью (атомная амплитуда γ вместо f). Структурные амплитуды G(hkl) квадратичной структуры можно записать в виде

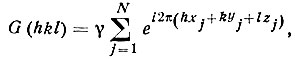
откуда следует, что F(hkl)=(f/γ)G(hkl).

С другой стороны, используя интегральную формулу структурной амплитуды типа (33), можно записать, что

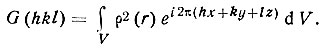
Подставив сюда (дважды) разложение р(r) в ряд Фурье, получим

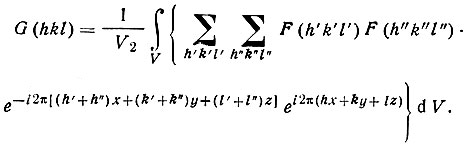
Интеграл по периоду экспоненциальной функции типа

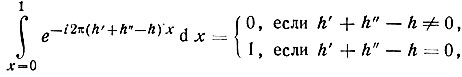
и из всех членов суммы остаются лишь те, которые удовлетворяют условиям

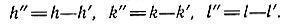
Окончательно имеем:

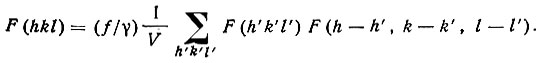(56)

Это равенство, найденное Сейром, связывает структурные амплитуды разных отражений в любой структуре, построенной из одинаковых атомов. Приближенно оно остается справедливым и в случае атомов с разной рассеивающей способностью. Это равенство является весьма общим, так как оно связывает все отражения, Даваемые кристаллом.

Из равенства Сейра вытекает, в частности, справедливость утверждения (53) о близости инварианта Φ⁽³⁾ к нулю для троек сильных отражений.

Действительно, умножив обе части равенства Сейра на F*(hkl), т. е. на F(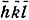), получим

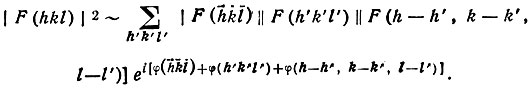
Наибольший вклад в сумму правой части равенства вносят те члены, которые имеют максимальную абсолютную величину, т. е. члены, составленные из трех сильных отражений. Итак, слева стоит вещественная положительная и притом большая величина, поэтому и в правой части для таких членов следует ожидать величины "почти вещественной", а это означает, что для таких отражений аргумент экспоненты

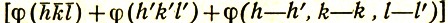
должен быть близок к нулю с модулем 2π. С другой стороны, нетрудно видеть, что отражения 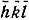, h'k'l' и h-h', k-k', l-l' образуют замкнутую систему: -H+Н'+(Н-Н')=0. Таким образом, мы снова получаем, но уже формально-математически, приближенное равенство Φ⁽³⁾≅0 (модуль 2π).

Мы получили вероятные значения фазовых инвариантов и вероятное соотношение между знаками структурных амплитуд для троек сильных отражений. Однако для практического использования этих соотношений важно знать, какова, собственно, вероятность их выполнения и как зависит эта вероятность от силы отражений. Это подводит нас к проблемам статистики рассматриваемых характеристик. Необходимо выяснить, как распределяются по величине структурные амплитуды, структурные произведения и фазовые инварианты.