Распределение структурных амплитуд и тройных структурных произведений в центросимметричных структурах

Каждый кристалл со структурой средней сложности дает несколько тысяч отражений. Это позволяет ставить вопрос о статистическом распределении структурных амплитуд, т. е. искать их функцию распределения P(F)dF- относительное (вероятное) число отражений, лежащих в разных интервалах от F до F+dF. Аналогичным образом должна существовать и функция распределения Р(Х_H' H')dX_H,H' по значениям Х_H,H'.

Начнем с функции распределения структурных амплитуд. Для того чтобы избавиться в кривой распределения плотности вероятности P(F) от вторичной зависимости, создаваемой систематическим уменьшением f_j с возрастанием индексов hkl (см. § 2 этой главы), перейдем от структурных амплитуд к так называемым нормализованным структурным амплитудам E(hkl):

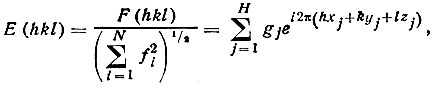(57)

где

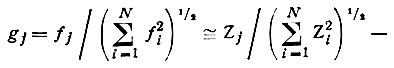
долевой коэффициент j-го атома в формуле для E(hkl). В силу приблизительного подобия f-кривых разных атомов долевые коэффициенты g_j практически не зависят от sin θ/λ, что и указано в формуле (58). Понятно также, что долевые коэффициенты всегда меньше единицы, а сумма их квадратов по всем атомам равна единице*. В центросимметричной структуре

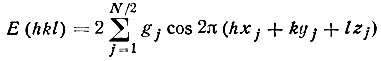(59)

или, в более короткой записи,

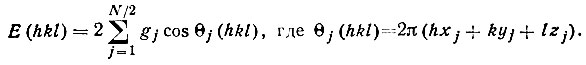
^* ( А. Вильсоном было показано, что среднеквадратическое значение структурной амплитуды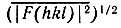 для любой структуры равно 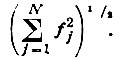. Следовательно, переход к нормализованным структурам амплитудам приравнивая среднеквадратичные значения амплитуд разных структур (делает их равными единице).)

Множество нормализованных амплитуд E(hkl) зависит от (N/2) 3 независимых параметров x_j, y_j, z_j. Эти параметры входят в (59) в виде сумм hx_j + ky_j + lz_j. Так как относительные координаты атомов х_j, у_j, z_j имеют разные значения, меньшие единицы, как правило, не сводящиеся к простым дробям периодов, то их суммы, взятые с разными целочисленными множителями h, k, l, приобретают смысл случайных чисел. Если учесть периодичность cos2π (hx+ky+lz) и свести все суммы hx_j+ky_j+lz_j к одному периоду, т. е. к области от 0 до 1, а также учесть, что общее число этих сумм равно числу отражений hkl, умноженному на число независимых атомов в ячейке N/2 (т. e. лежит в области десятков тысяч), то имеются все основания считать, что в общем массиве нормализованных структурных амплитуд E(hkl) суммы hx_j+ky_j+lz_j распределяются от 0 до 1 равномерно. Это положение очень существенно, так как позволяет применить к распределению Р(Е) по разным значениям амплитуд Е центральную теорему А. М. Ляпунова теории вероятности. Согласно этой теореме распределение Р(Е) должно быть близко к гауссовому.

Из (59), кроме того, следует, что среднее значение E(hkl) равно нулю 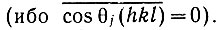Поэтому распределение Р(Е) должно быть симметричным относительно положительных и отрицательных значений E(hkl).

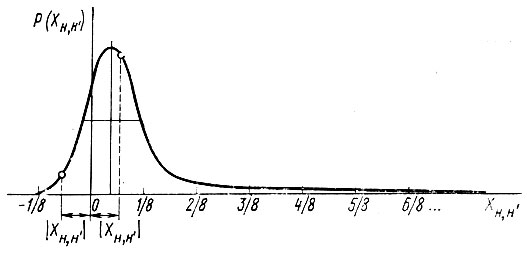
Рис. 50. Распределение вероятности Р(Х_H,H') разных значений структурных произведений X_H,H' в случае центросимметричного кристалла (по оси абсцисс отложены Х/Х_max)

Составим теперь все возможные тройные структурные произведения:

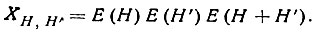(60)

Рассмотрим вероятностное распределение Р(Х)^* . Оно также должно быть близко к гауссовому. Легко, однако, понять, что среднее значение X_H,H' уже не равно нулю, а всегда (в любой структуре) положительно^**.

^* (Здесь и далее понятие структурного произведения и обозначения Х_H,H' относятся к нормализованным структурным амплитудам.)

^** (Действительно, при подстановке трех сумм типа (59) в выражение для Х_H,H' возникнут члены двух типов: при r≠s≠t тройные произведения косинусов разных аргументов cos θ_r*cos²θ'_s *cos (θ_t + θ'_t), средние значения которых равны нулю, а при r =s= t произведения квадратов косинусов cos²θ_r*cos²'_r, средние значения которых равны + 1/4. Детальнее см.: Порай-Кошиц М. А. Практический курс рентгеноструктурного анализа. М., Изд-во МГУ, I960. Т. 2. С. 282-283. )

Следовательно, гауссово распределение Р(Х) сдвинуто в сторону положительных значений X (рис. 50).

Распределение имеет, конечно, лишь приблизительно гауссову форму, так как произведение Х_H,H' не может быть больше, чем

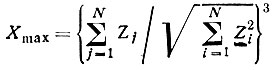
[см. формулу (57) для максимального значения всех

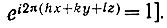
Исходя из обычных условий экстремальности

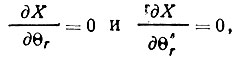
А. И. Китайгородским было показано, что кроме тривиального верхнего пределах Х_max существует и нижний предел X_min =-1/8*X_max. Это показывает, что распределение Р(Х) сдвинуто в сторону положительных X довольно сильно. Кроме того, из этого следует, что при |Х|>>1/8|X_max| оно обязано быть положительным. (Правда, это последнее условие означает, грубо говоря, что нормализованные структурные амплитуды всех трех отражений Е(Н), E(H'), E(H+H') должны быть близки к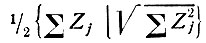

т. е. к половине максимального значения E, а такие большие значения Е достигаются достаточно редко.)

Сказанное означает также, что при заданном значении |Х_H,Н' | <1/8*X_max оно чаще бывает положительным, чем отрицательным, что и отражено в вероятностном соотношении Захариазена. Вероятность положительности и соответственно отрицательности X при заданном модуле |Х| определяется очевидными формулами:

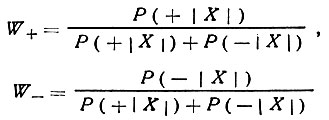
или, что то же,

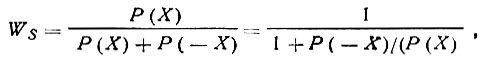
где S - знак структурного произведения X.

Само гауссово распределение имеет вид

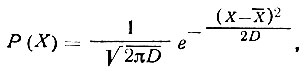(61)

где 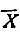- математическое ожидание (среднее значение X в распределении), 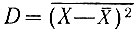- дисперсия распределения. Нетрудно видеть, что

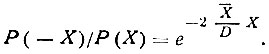
Обозначив (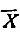/D)X=A, получим

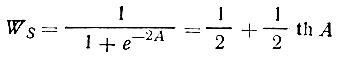(62)

(th - обозначение тангенса гиперболического).

Выражение (62) дает вероятность W₊, если Х_H,H положительно, и вероятность W_-, если оно отрицательно.

Значения 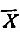и D можно рассчитать, используя выражения (59) и (60)^*. Такой расчет дает

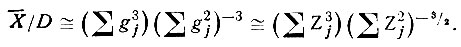
В соответствии с общепринятым обозначением моментов 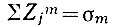имеем

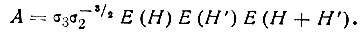
^* ( См., например: Порай-Кошиц М. А. Практический курс рентгеноструктурного анализа. М., Изд-во МГУ, 1960. Т. II. С. 283-284.)

Соотношение Захариазена справедливо с вероятностью W₊(A). Согласно (62) оно тем более достоверно, чем больше по модулю нормализованные амплитуды всех трех отражений - участников структурного произведения. То же с очевидностью следует и из рис. 50.

Г. Хауптман и Дж. Карль предложили использовать для определения знака отражения H не только триплетное, но и ряд других статистических соотношений и вывели формулы вероятности их выполнения. Согласно этим представлениям Е(Н) определяется знаком четверной суммы:

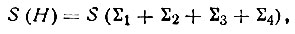
где

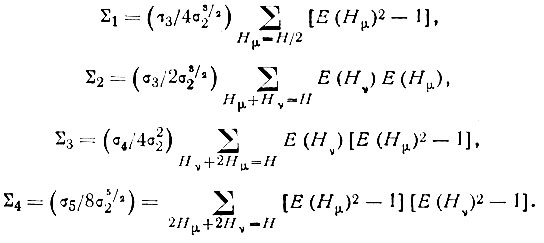
Член ∑₂ соответствует триплетному соотношению Захариазена.

В настоящее время формулы Хауптмана-Карля представляют скорее исторический, чем практический интерес.