
Функции распределения фазовых инвариантов в не центросимметричных структурах
Обобщенное понятие структурного произведения можно ввести и для нецентросимметричных структур: X(n)=E(Н1)Е(Н2) ...Е(Нn), где Н1+Н2+...+Нn= 0. Или в короткой записи Х(n)= | Х(n) |eiΦ(n), где Φ(n)=φ(H1)+φ(H2) + ...+(Hn) - фазовый инвариант.
В не центросимметричных структурах и F(hkl), и Х(n) - комплексные величины. Речь, следовательно, должна идти о распределении в двумерном комплексном поле: требуется определить плотность вероятности в точке комплексного поля с заданными вещественной и мнимой компонентами F(hkl) (или Х(n)). Рассматривая плотность вероятности в некотором заданном кольцевом поясе поля, т. е. при заданном значении модуля |F| (или |X(n)|;, получим вероятное распределение начальных фаз отражения ф(Я) (или, соответственно, значений инвариантов Φ(n)). Для самых структурных амплитуд результат известен априори: все начальные фазы φ(Н) равновероятны. Для структурных произведений ситуация будет уже иной, в чем мы уже убедились, рассматривая значения Φ(3) и Φ(4) для больших по модулю амплитуд. В общем же случае Р(Φn) зависит не только от модуля |X(n)|, но должно быть разным для структурных произведений разного ранга n.
Для тройных структурных произведений
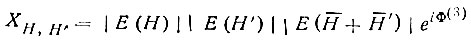
распределение Р(Φ(3)) для заданного значения модуля |ХH,H'| имеет вид
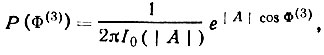 (63)
(63)
где I0(|A|) - модифицированная функция Бесселя второго рода, а
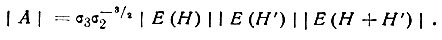
При Φ(3)= 0 Р(Φ(3)) имеет максимальное значение, равное (2πI0(|А|)-1e|A|, и поскольку cos Φ(3) симметричен относительно Φ(3) = 0, то и Р(Φ(3)) понижается симметрично в области положительных и отрицательных значений Р(Φ(3)). Чем больше |A|, т. е. |ХH,H' |, тем больше максимальное значение Р(Φ(3)) и тем быстрее убывает эта величина с увеличением Φ(3) (рис. 51).
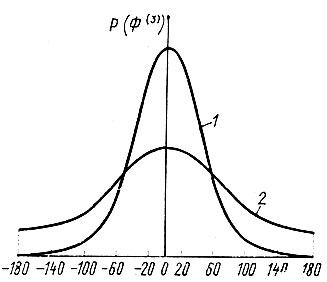
Рис. 51. Распределение вероятности Р(Φ(3)) разных значений триплетного фазового инварианта Φ(3) при двух разных значениях аргумента |А|=σ3σ2-3/2|XH,H'|:1-A=2,316; 2-А=0,731
Формулу (63) можно получить следующим образом. Представим ХH,H', виде x+iy. И вещественная, и мнимая части должны иметь распределения, близкие к гауссову:
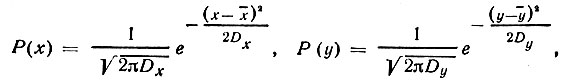
где 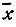 и ӯ - средние значения; Dx и Dy - дисперсии распределений. Поскольку Dx=Dy [распределения Р(х) и Р(у) должны быть одинаковыми], то вероятность того, что х лежит в области от х до x + dx и одновременно у в области от у до y + dy,
и ӯ - средние значения; Dx и Dy - дисперсии распределений. Поскольку Dx=Dy [распределения Р(х) и Р(у) должны быть одинаковыми], то вероятность того, что х лежит в области от х до x + dx и одновременно у в области от у до y + dy,
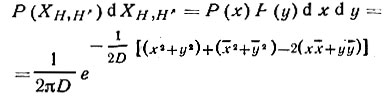
Но
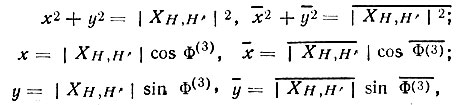
а следовательно,
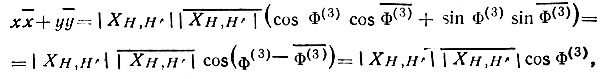
поскольку
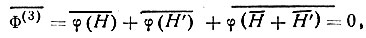
Учитывая эти соотношения, получаем
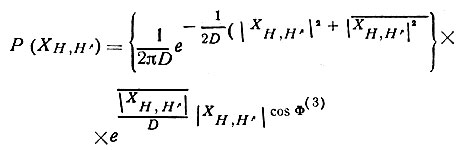
Так же, как и в центросимметричном кристалле,
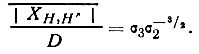
Поскольку нас интересует лишь распределение по ф(3) при заданном модуле |ХH,H' |, часть выражения, стоящая в фигурных скобках, играет роль константы
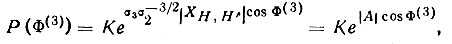
где 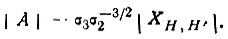
Величина К рассчитывается из условия
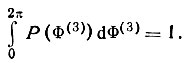
Следовательно,
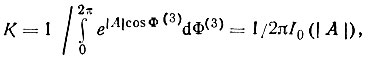
где I0(|A|) - модицифированная бесселева функция второго порядка аргумента |A|. Окончательно имеем
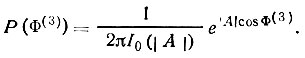
Аналогичным образом можно вывести формулы для вероятного распределения фазового инварианта Φn любого ранга n. Для этого достаточно ввести понятие структурного произведения n-го ранга
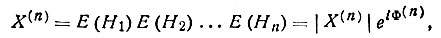
снова использовать тот факт, что распределение P(Xn)-это распределение случайных величин в двумерном (комплексном) поле, а Р(Φn)-это распределение Xn по его фазовым аргументам при заданном модуле (т. е. распределение в кольцевом поясе комплексного поля), учесть нормировку интегральной вероятности к единице, и мы получим формулу, аналогичную (63):
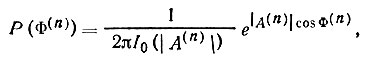
где 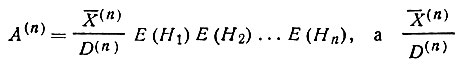 сводится к определенной комбинации моментов
сводится к определенной комбинации моментов 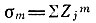
разных рангов m≤n, зависящей от ранга n рассматриваемого инварианта.
В частности, распределение инварианта Φ4 для фазового квартета можно написать в виде
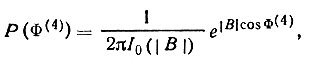 (64)
(64)
где 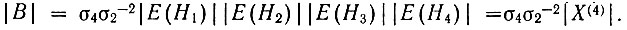
Как и в случае X3, при любом |X4| наиболее вероятно нулевое значение инварианта Φ4, и при этом сама вероятность Р(Φ4) тем выше, чем больше по модулю структурное произведение | X4 |.
В структуре с одинаковыми атомами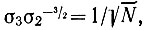 ,а σ4σ2-2=1/N. Поэтому при прочих равных условиях вероятность Р (Φ4)max ниже, чем Р(Φ3)max.
,а σ4σ2-2=1/N. Поэтому при прочих равных условиях вероятность Р (Φ4)max ниже, чем Р(Φ3)max.
Без дополнительных данных о других отражениях она, как правило, не слишком велика. Чтобы повысить Р(Φ4)max можно привлечь помимо четырех отражений, образующих квартет H1+H2+H3+H4 = 0, еще три отражения H5=H1 +H2, H6= H1+H3, H7= H2+H3, как эта было сделано выше. Анализ показывает, что функция распределения для основного квартета 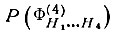 существенно зависит от нормализованных амплитуд дополняющих отражений. Если |E(H5)|, |E(H6)| и |Е(Н7)| все велики, наиболее вероятным снова является нулевое значение ΦnH1…H4. Но если амплитуды дополняющих отражений уменьшаются, то максимум
существенно зависит от нормализованных амплитуд дополняющих отражений. Если |E(H5)|, |E(H6)| и |Е(Н7)| все велики, наиболее вероятным снова является нулевое значение ΦnH1…H4. Но если амплитуды дополняющих отражений уменьшаются, то максимум 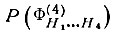 смещается с нулевого значения; возникают два симметрично расположенных максимума при некоторых промежуточных значениях ± Φn. При малых значениях дополняющих амплитуд максимумы смещаются в точки ±π (рис. 52). В предельном случае, когда |Е(Н5) | = |E(H6) |=|Е(Н7)|=0, формула имеет вид
смещается с нулевого значения; возникают два симметрично расположенных максимума при некоторых промежуточных значениях ± Φn. При малых значениях дополняющих амплитуд максимумы смещаются в точки ±π (рис. 52). В предельном случае, когда |Е(Н5) | = |E(H6) |=|Е(Н7)|=0, формула имеет вид
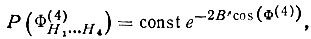
где
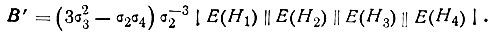
При
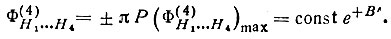
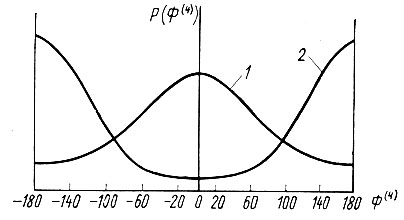
Рис. 52. Распределение вероятности Р(Φ4) разных значений квартетного фазового инварианта Φ4: 1 - при | Е1 | =1,408, |E2| =1,592, |E3|=2,672, |E4| = 1,770 (B=0,731) и не учете других отражений; 2 - при тех же значениях |E1|, |E2|, |E3| и |E4| и учете отражений Н5=Н1 + Н2, H6=H1+H3 и H7 = H2+H3 с | Е5 | =0,157, |E6| =0,385 и |E7|=0,425
Полученный результат на первый взгляд представляется странным в свете того чисто качественного анализа квартета волн плотности, который был предложен выше (см. рис. 49, б). В действительности, однако, это не совсем так. Условие Φn=π означает, что четвертая волна плотности H4 телесно-диагональная по отношению к трем независимым H1,H2 и H3, проходит через максимумы А не гребнями, а впадинами, тогда как гребни приходятся на середины отрезков между максимумами А (рис. 53, а), и если амплитуда |Е(Н4)| достаточно велика (больше, чем амплитуды |E(H1)|, |Е(Н2)|, |Е(Н3)|, то она не только ослабляет ложные минимумы В, но и создает максимумы в точках А' (одновременно ослабляя максимумы А). Но в этом случае дополняющие волны плотности H5=H1+H2, H6=H1+H3 и H7=H2+H3 должны иметь небольшие амплитуды, чтобы не уничтожать ни максимумы А, ни максимумы А' (см. рис. 49, в). И наоборот, по той же причине отражения с индексами 2Н1+ 2Н2, 2Н1+ 2Н3 и 2H2+2H3 должны быть сильными, ибо они отвечают волнам плотности, проходящими гребнями и через максимумы А, и через максимумы А'. К тому же они уничтожают отрицательный минимум в точке В, созданной волной H4 (рис. 53, б).
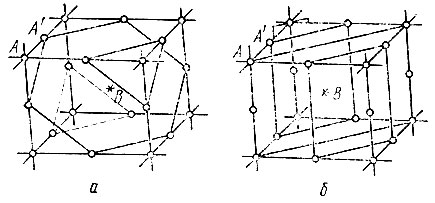
Рис. 53. Схема пересечения гребней плотности, отвечающей замкнутой системе из четырех сильных отраженийH1, Н2, H3 и H4= -Н1-H2-H3 при учете слабых отражений H5=H1+H2, H6=H1+H3 и Н7= Н2+Н3a - волны плотности Н1, Н2, Н3 и H4 при Ф(4) = A; б - волны плотности 2Н1+2Н2
Из сказанного очевидно, что наиболее вероятное значение квартетного инварианта Φ4 зависит от амплитудных значений отражений, так или иначе дополняющих четверку рассматриваемых. Такое привлечение амплитуд дополняющих отражений для правильной оценки наиболее вероятного значения фазового инварианта Φ4 основного квартета было названо принципом окрестностей. Отражения H5, H6 и H7 составляют вторую окрестность квартета H1+H2+H3+H4 = 0. Третью его окрестность можно выделить, учтя еще два независимых сильных отражения H8 и H9, образующих второй квартет H1+H2+H8+H9 = 0, И отражения типа H10=H1+H8, H11=H2+H8, H12=H3+H8, H13=H4+H8 (остальные парные сочетания дают те же отражения). Соответствующие формулы совместного распределения вероятности Р (Ф(4)1,2,3,4 Ф(4)1,2,8,9) мы рассматривать не будем*.
* (См. сб.: Прямые методы в рентгеновской кристаллографии/Под ред. М. Лэдда и Р. Палмера. М., Мир, 1983. С. 168-190.)
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'