Практические приемы определения знаков структурных амплитуд в случае центросимметричного кристалла

Для центросимметричного кристалла требуется определить лишь знаки структурных амплитуд. Главный источник для решения этой задачи - вероятностное соотношение Захариазена

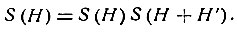
Для начала допустим, что знаки структурных амплитуд некоторых наиболее сильных отражений каким-то образом уже определены, и среди них имеется несколько пар с индексами, различающимися на одну и ту же величину H₀. Обозначим их H_i и H_i + H₀.

Понятно, что каждая комбинация позволяет определить вероятный знак отражения H₀, если последнее не относится к очень слабым. И если все такие комбинации или подавляющее большинство из них дают один и тот же знак, статистический результат можно считать достаточно убедительным. Иначе говоря, знак отражения H₀ определяется соотношением

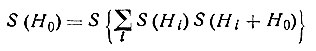(65)

(буква S перед фигурной скобкой означает, что используется не сама сумма по i, а только ее знак), причем знак считается найденным, если в фигурных скобках стоит достаточно большая по модулю величина.

Если использовать значения |E(H₀)|, |E(H_i)| | E(H_i+H₀) | в качестве весовых множителей "убедительности", то можно воспользоваться более действенной формулой

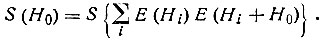(66)

Формулу (66) можно вывести из равенства Сейра для структуры, построенной из одинаковых точечных атомов с атомными амплитудами, равными долевым коэффициентам g, и соответствующей "квадратизованной" структуры с атомными амплитудами η:

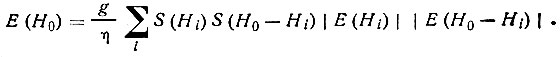
Поскольку главную роль в правой части равенства играют те члены сумм, в которых одновременно участвуют два сильных отражения, при оценке знака правой части остальными членами можно пренебречь. Учитывая, что в центросимметричной структуре 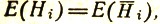получаем формулу (66).

Еще правильнее воспользоваться в качестве весовых множителей вероятностями W_s [формула (62)]:

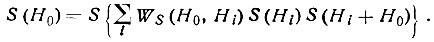(67)

Если знак S(H₀) определяется достаточно убедительно, то отражение Н₀ можно присоединить к массиву базовых отражений, уже известных по знаку, и использовать при составлении других структурных произведений.

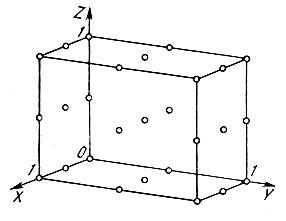
Рис. 54. Расположение центров инверсии в центросимметричной структуре с примитивной решеткой

Естественно, что чем более слабые единичные амплитуды мы будем использовать при составлении комбинаций, тем менее достоверными будут результаты и тем чаще придется сталкиваться с неубедительной (противоречивой) статистикой. Поэтому лучше всего заранее ограничиться лишь определенной частью наиболее сильных отражений (выделить массив "определяемых" отражений) и пытаться установить знаки большинства из них, с тем чтобы по полученным результатам (используя лишь те отражения, знаки которых удалось определить) рассчитать распределение электронной плотности в первом приближении (см. § 6).

Таким образом, основная, наиболее сложная задача заключается в выборе знаков начальной ("базовой") группы сильных отражений, исходной для использования статистического равенства Захариазена.

Возможны различные способы решения этой начальной задачи. Здесь будет рассмотрен один способ, простой по идее, но трудоемкий по числу операций,- метод перебора. Такой подход стал практически возможным лишь после создания достаточно емких по памяти и быстродействующих ЭВМ.

Предварительно отметим следующее. В центросимметричной структуре с примитивной решеткой, принадлежащей к триклинной, моноклинной или ромбической сингонии, на каждую ячейку приходится по 8 центров инверсии с координатами, равными 0 или 1/2 по каждой из трех осей (рис. 54). Из общей формулы структурной амплитуды центросимметричного кристалла (41) следует, что при переносе начала координат ячейки из одного центра инверсии в другой, смещенный на 1/2 трансляции по X, все отражения hkl с нечетными h изменят знак на обратный. При аналогичном смещении по Y знак изменяют все отражения с нечетными k при смещении по Z - с нечетными l. Это означает, что трем любым отражениям hkl (одному с h нечетным, другому с k нечетным и третьему с l нечетным) знаки можно приписать произвольно; выбор знаков лишь фиксирует начало координат в одном из восьми центров инверсии. Естественно, что эти три отражения следует выбрать из числа наиболее сильных (с большими |Е(Н)|)^*.

^* (Сказанное относится к общему случаю - пространственным группам низших сингоний с примитивными решетками. Добавление Других элементов симметрии видоизменяет (по довольно сложным правилам) правила произвольного выбора знаков и сокращает число отражений, для которых это можно делать.)

Конечно, три отражения - основа, недостаточная для развития статистической знаковой цепочки. Как показывает опыт, такой основой для структур средней сложности может служить базовая группа из 7-11 сильных отражений.

Идея метода перебора состоит в следующем. Задав произвольные знаки трем отражениям и дополнив базовую группу еще 4-8 сильными отражениями, исследователь (вычислительная машина) составляет все возможные варианты комбинаций их знаков и для каждого из знаковых вариантов (базовой группы отражений) проводит по схеме Захариазена статистическую обработку большой группы в 150-300 "определяемых" отражений. Всего требуется рассмотреть 2ⁿ знаковых вариантов, т. е. 16 при n=4, 64 при n=6, 256 при n=8.

Отметим еще следующее. Сами комбинации троек отражений H, Н' и H+H', два из которых входят в постепенно расширяющуюся "базовую" группу, а одно - в более широкую группу "определяемых" отражений, не зависят от выбора знаков в исходной базовой группе (это комбинации индексов!). Поэтому, чтобы сократить затрату машинного времени, вначале удобно приписать знакам базовых отражений условные символы: а, b, с и т. д. Тогда определяемые отражения, вошедшие в тройки, получат обозначения, состоящие из комбинаций таких символов^*.

^* (Описываемый здесь метод близок к использованному в программе LSAM (Logical Symbolic Addtion Method), входящий в известный комплекс MULTAN - 1975.)

Поясним это примером. Предположим, что базовую группу составляют следующие "сильные отражения":

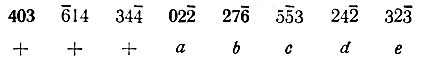
(для первых трех приняты знаки+ , остальным приписаны символы а, b, с, d, е). Предположим далее, что в определяемую группу среди других сильных отражений попали отражения

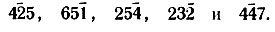
Тогда (для тех отражений, которые выше выделены жирным шрифтом) можно составить следующие комбинации S (H₁+Н₂)S (Н₂)=S(Н₁):

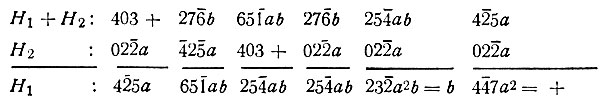
В последних двух столбцах использовано очевидное положение, что квадрат любого "знака" положителен. Это приводит, в частности, к заключению, что отражение 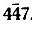имеет, вероятно, положительный знак. Отметим также, что отражение 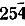дважды получило символ ab, что повышает вероятность правильности такого заключения.

Продолжая этот процесс, можно составить символическую запись (в виде произведения двух или нескольких буквенных символов) большинства определяемых отражений. Для каждого (или почти для каждого) из них будет получено несколько вариантов буквенных обозначений, поскольку одно и то же отражение Н₀ можно получить на основе многих пар Н_i и Н_i+Н₀. Естественно, что при подстановке вместо буквенных обозначений знаков +1 или -1 для многих из них будут возникать существенные или малосущественные (например, девять раз +1, один раз - 1) противоречия. Понятно, что в каждом из возможных исходных вариантов (256 вариантов при n = 8) для знаков базовых отражений убедительно определяются знаки разного числа "определяемых" отражений.

Контрольный расчет распределения р(xyz) для 256 вариантов - процедура довольно трудоемкая даже для современной вычислительной машины, а анализ такого числа трехмерных распределений р(xyz) представляет собой и вовсе непосильную задачу. Поэтому приходится использовать более простые, хотя и менее обоснованные "интегральные" критерии выбора правильного варианта. В основе этих критериев лежит полуэмпирическое "правило убедительности": предполагается, что реальная структура должна отвечать одному из тех вариантов, для которых вероятностные соотношения Захариазена удовлетворяются в максимальной степени. Такими критериями могут служить:

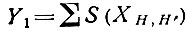1. - сумма знаков всех структурных произведений, как положительных, так и отрицательных, получаемых в каждом из вариантов;
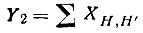2. сумма самих структурных произведений;
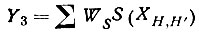3. - сумма знаков Х_H,H' с учетом вероятности правильного определения знака.

"Наилучшими" должны быть варианты, дающие максимальные значения Y₁, Y₂ и Y₃.

Другой критерий относится к типу фактора расходимости

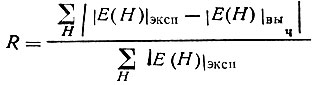
(суммирование по всем сильным отражениям H), причем в качестве |E(H)|_выч берутся значения |E(H)|, полученные по уравнению Сейра

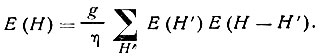
Суммирование по H' ограничивается, естественно, только теми сильными отражениями H' и H-H', для которых в данном варианте удалось установить знаки амплитуд. Наилучшими следует считать те варианты, которые дают наименьшие значения критерия расходимости R^*.

^* (Коэффициент g/η определяется из соотношения )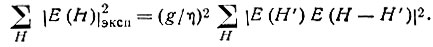

Третий удобный критерий также основан на равенстве Сейра, но уже применительно к отсутствующим или очень слабым отражениям H. Если, E(H) ≅0 то и сумма ΣЕ(Н')E(H-H')) по сильным отражениям не должна резко отличаться от нуля. Тем более это относится к совокупности всех отражений H с Е(Н), близким к нулю. Поэтому правильными следует считать те знаки отражений H' и H-H', которые приводят к одному из наименьших значений суммы

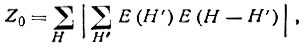
где внешнее суммирование проводится по отражениям H, имеющим низкую или нулевую интенсивность.

Опыт показал, что критерий Z₀ обычно несколько эффективнее, чем Y или R.

С помощью интегральных критериев обычно отбираются несколько наиболее правдоподобных вариантов знаков, и для каждого из них проводится расчет электронной плотности (при учете в ряду Фурье лишь тех отражений, которым удалось приписать знаки).

Как правило, на этой стадии рассчитывают не обычную электронную плотность, а ее аналог - ряд Фурье с нормализованными амплитудами Е(Н) вместо полных F(H) в качестве коэффициентов ряда (так называемый E-синтез). Такой синтез соответствует структуре с точечными атомами.

Поскольку в расчете р_E(xyz) использовалась лишь часть отражений^*, распределение, естественно, не может выявить всех деталей структуры. Но тем не менее правильный вариант должен проявить себя стереохимической разумностью размещения максимумов - правдоподобием в межатомных расстояниях и валентных углах. Дальнейшая обработка проводится по описанной схеме последовательных приближений в F(hkl) и p(xyz)^**

^* (Менее 150-300, поскольку статистика не может быть убедительной для всех отобранных для обработки "определяемых" отражений.)

^** (Задача отбора правильного варианта становится более сложной, если состав исследуемого соединения (в частности, присутствие в нем определенных химических группировок) заранее неизвестен или был определен неправильно. Но решение задачи в таких условиях представляется особенно заманчивым и почетным.)