Практические приемы определения начальных фаг структурных амплитуд в случае не центросимметричного кристалла

Как и в случае центросимметричного кристалла, мы рассмотрим лишь тройные структурные произведения (хотя на практике используются и другие, более сложные инварианты, и прежде всего квартеты с учетом второй окрестности). Простейший метод определения начальных фаз на основе тройных фазовых инвариантов- все тот же метод перебора вариантов^*.

^* (Этот метод использован в основной части комплекса MULTAN-1975, относящейся к не центросимметричным структурам (MULTAN - Multiple-tangens formula method).)

Выбирается небольшая группа базовых отражений. Трем из них приписываются нулевые значения начальных фаз. Это фиксирует начало координат. Начальные фазы остальных задаются с точностью до 90°, например 1/4π, 3/4π, 5/4π и 7/4π. Это значит, что для каждого базового отражения имеется не 2 возможных знака, а 4 возможные (и, естественно, резко огрубленные) начальные фазы. Следовательно, перебору подлежат не 2ⁿ, а 4ⁿ вариантов. Для каждого варианта начальных фаз базовой группы по формуле 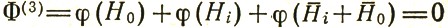(модуль 2π) определяются приближенные фазы "определяемых" отражений H₀.

Для уточнения приближенных значений фаз, полученных из пошагового применения соотношения (52) на основе округленных фаз базовых отражений, чаще всего используют "тангенс-формулу"

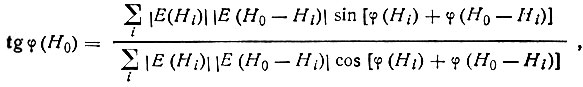(68)

являющуюся аналогом формулы (66) для центросимметричного случая.

Формула (68), как и формула (66), вытекает из равенства Сейра, выведенного для структуры с одинаковыми точечными атомами, дающими атомные амплитуды, равные долевым коэффициентам g. Для не центросимметричной структуры равенство выглядит так:

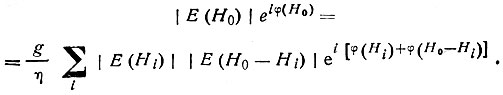
Вещественная часть дает равенство

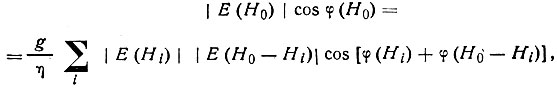
мнимая - равенство

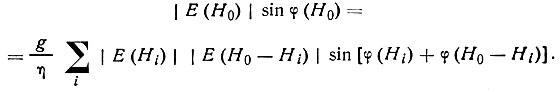
Пренебрегая всеми членами сумм по i, кроме тех, которые содержат произведения "сильных" отражений |E(H_i)| и |Е(H₀- H_i) |, и разделив второе равенство на первое, сразу получим тангенс - формулу (68).

Чтобы в процессе пошагового определения фаз отсеять недостаточно убедительные заключения, каждый шаг следует контролировать расчетом вероятности выполнения условия Φ⁽³⁾ = 0 по формуле (63).

Далее по интегральным критериям типа Y₂, R и Z₀ производится сопоставление всех исходных вариантов и отбираются несколько наиболее "убедительных" для последующего анализа распределения электронной плотности.

Понятно, что увеличение числа вариантов по сравнению с центросимметричным случаем (4ⁿ) ведет к значительному увеличению трудоемкости расчетов, а огрубление начальных фаз базовой группы отражений - к понижению убедительности статистики. Поэтому для дальнейшего подробного анализа отбирают 10-20 вариантов начальных фаз, лучших по интегральным критериям.

Естественно, что вся работа по поиску начальных фаз (так же как и знаков структурных амплитуд в центросимметричных кристаллах) проводится на ЭВМ с помощью специальных программ. Современные программы определения начальных фаз прямыми методами включают не только анализ тройных фазовых инвариантов, но и четверных с учетом второй, а иногда и более дальних окрестностей и другие алгоритмы поиска начальных фаз, не обсуждавшиеся выше.

В частности, в последних версиях программы MULTAN и SHELX использован комбинированный метод поиска фаз на основе тройных и сопряженных с ними квартетных фазовых инвариантов. Стоит также отметить подходы, основанные на несколько иной начальной стадии поиска фаз. Вместо разбиения поля фаз на равные интервалы с шагом π/2 используется идея "случайных" фаз или близкая к ней идея задания исходного набора фаз с помощью так называемых магических целых чисел. Не касаясь существа и деталей этих подходов, отметим, что они оказались более эффективными, чем разбиение поля фаз на равные интервалы. Связано это, по-видимому, с тем что при округлении фаз до n π/4, n - 1, 3, 5, 7, часто получается много самосогласующихся триплетов, хотя реальные фазы и не имеют ничего общего с заданными в очередном варианте.

Хотя в целом расшифровка не центросимметричной структуры статистическим методом представляет собой задачу, несравненно более сложную, чем исследование тем же методом центросимметричной структуры. Тем не менее в настоящее время она решается с помощью системы вполне стандартных приемов (запрограммированных в структурных комплексах программ) для структур, содержащих вплоть до 150-200 атомов в независимой области элементарной ячейки.