Паттерсоновский поиск фрагмента структуры с учетом статистических фазовых соотношений

Выше уже упоминалось о возможности использования априорных знаний о возможном строении структурных фрагментов при расшифровке паттерсоновских распределений. Первая стадия - поиск ориентации заданного фрагмента остается в прежнем виде: он проводится на основе анализа межатомной функции в ближайшем окружении начала координат пространства P(uvw). Вторую стадию - поиск трансляционного положения фрагмента в ячейке можно видоизменить и значительно упростить, если опираться на требование минимальности триплетных фазовых инвариантов Φ⁽³⁾ для троек сильных отражений.

Будем перемещать фрагмент параллельно самому себе в разные точки ячейки. Для каждого из положений рассчитаем вклад фрагмента в структурные амплитуды Е_фp(Н) "определяемых" (а следовательно, сильных) отражений. Предполагается, что заданный фрагмент структуры существенно "помогает" тройным произведениям, составленным из сильных отражений, иметь большие значения, а структурным инвариантам Φ⁽³⁾ быть близкими к нулю. Поэтому "наилучшими" можно считать те позиции фрагмента в ячейке, которые дают наименьшие значения сумм 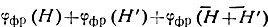по всем рассматриваемым триплетам. Наименьшим значениямΦ⁽³⁾ отвечают наибольшие значения cos Φ⁽³⁾_фр. Поэтому в качестве критерия наилучшей позиции фрагмента можно взять максимальное значение взвешенной суммы:

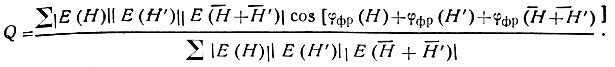
Нахождение максимума Q требует расчета φ_фp(H) всех нужных отражений при всех перемещениях фрагмента по ячейке. Эта работа не столь трудоемкая, как это может показаться с первого взгляда. Если для некоторого исходного положения фрагмента его вклад в амплитуду отражения Н равен Е⁰_фр(Н), то параллельный перенос фрагмента на вектор Δr требует лишь уменьшения этой величины на ехр(2πНΔr):

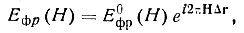
ибо все атомы смещаются на один и тот же вектор. Расчет вклада фрагмента в структурную амплитуду фактически производится лишь один раз. Впрочем, надо помнить, что его надо провести и для всех остальных фрагментов, размноженных элементами симметрии структуры, так что окончательный вид формулы определяется характером тригонометрических преобразований формулы структурной амплитуды в присутствии элементов симметрии (см. § 4, гл. IV). Целью расчета является извлечение из комплексной величины Е_фр(Н) ее аргумента φ_фр(Н) и последующее сопоставление величины Q при разных положениях фрагмента.

Такая процедура поиска позиции заранее заданного фрагмента уже опробована и включена в качестве дополнения в комплекс программ SHELX-84 под кодовым названием PATSEE.