Область применения статистического метода

Центральная теорема А. М. Ляпунова, положенная в основу вывода статистических соотношений, строго говоря, справедлива лишь при равноценности вкладов независимых компонентов 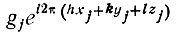в суммарное распределение E(hkl) и при равномерном распределении аргументов hx_j + ky_j+lz_j по тригонометрическому кругу при переборе hkl.

Первому требованию в наибольшей степени подчиняются структуры с одинаковыми или почти одинаковыми атомами (близкие Z_j), второму - структуры, атомы которых имеют достаточно иррациональные координаты, с тем чтобы при переборе hkl суммы 2n(hx_j+ ky_j+lz_j) могли приобрести любые значения, а не набор нескольких рациональных долей периода. Из этого следует, что наилучшие результаты статистический метод должен Давать применительно к структурам молекулярных органических соединений, где все атомы мало различаются по рассеивающей способности, а межатомные расстояния (валентные и межмолекулярные) практически не связаны с параметрами решетки. К структурам с тяжелым атомом метод применим лишь при условии, что тяжелые атомы распределены по ячейке достаточно не-равномерно. Статистический метод вовсе неприменим там, где тяжелые атомы (или тем более все атомы) размещаются в виде равномерной трехмерной сетки. Например, в кристалле NaF атомы Na и F имеют координаты 0, 0, 0 и 1/2, 0, 0; и аргументы 2n(hx_j + ky_j + lz_j) при переборе h, k, l приобретают лишь два значения тригонометрического круга: 0 и я. В этих условиях не может быть и речи о какой-либо близости набора E(hkl) к гауссовому распределению^*.

^* (Фактически в этой структуре все E(hkl) с h, k, l четными равны g_Na+g_F, а с h, k, l нечетными g_Na-g_F. Если Na находится в начале координат, знаки всех отражений положительны. )