§ 9. Метод минимизации структурного функционала

Структурным функционалом называют величину

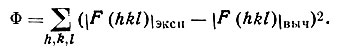(69)

Если в ячейке кристалла имеется n симметрически независимых атомов, то F (hkl) _выч, а следовательно, и само Φ является функцией 3n переменных. Функционал, следовательно, можно рассматривать как функцию, распределенную в пространстве 3/r-измерений. Требуется найти такие значения координат, при которых F (hkl)_выч были бы максимально близки к F(hkl)_эксп, т. е. найти глобальный (наиболее глубокий) минимум функционала Φ в этом пространстве, начав движение к нему из некоторой произвольной точки.

Решение задач такого типа возможно только с применением ЭВМ. Идея метода решения, предложенная И. М. Гельфандом и получившая название метода оврагов, заключается в следующем.

"Движение" начинается из точки пространства функционала, отвечающей некоторому произвольному набору координат независимых атомов, и производится все время в направлении наиболее крутого спуска. Величина шага должна быть достаточно большой, чтобы миновать мелкие неровности поверхности Φ (см. левую часть рис. 55, а) и чтобы общее время решения задачи не оказалось чрезмерно длительным. Однако шаг не должен быть настолько большим, чтобы возникла возможность проскочить глобальный минимум или достаточно мощный овраг, ведущий к этому минимуму. В новой точке снова определяется направление градиента, делается второй шаг и т. д., пока движение не замкнется в некоторой узкой области, отвечающей минимуму функционала (правая часть рис. 55, а). По идее каждый последующий шаг должен приводить к уменьшению величины ф. Возрастание Φ на одном из шагов означает проскок через овраг на его противоположный склон (рис. 55, б). В этом случае следует повторить последний шаг, сократив его размер, например, вдвое. Нащупав таким образом дно оврага, можно двигаться дальше прежними "полными" шагами. Наоборот, если движение "замкнулось" при некотором, явно недостаточно низком значении Φ, то требуется увеличить шаг, чтобы выйти за пределы локального минимума (рис. 55, в).

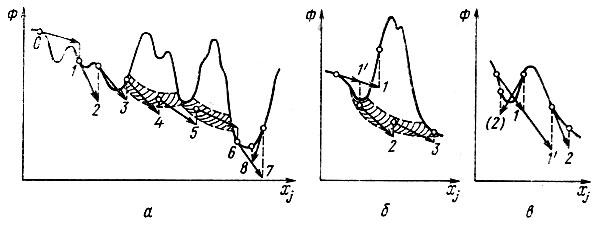
Рис. 55. Иллюстрация метода оврагов:а - траектория движения, приводящая к глобальному минимуму; б - проскок через овраг, сокращение шага; в -замыкание в локальном минимуме,увеличение шага

Вполне понятно, что метод оврагов применим только к функциям, удовлетворяющим основному требованию: к глобальному минимуму ведут "овраги" (по терминологии И. М. Гельфанда функция должна быть "хорошо организованной"). Применительно к структурным задачам функционал проявляет себя как хорошо организованная функция лишь при условии, что независимые переменные относятся не к отдельным атомам, а к большой массе атомов сразу и если число переменных не слишком велико. Этому требованию отвечают главным образом структуры, составленные из полиатомных фрагментов известной конфигурации. Для примера на рис. 56 изображена молекула 1,3,5- тринитробензола. Форма и размеры бензольных колец, равно как нитрогрупп, хорошо известны. Конфигурация молекулы описывается, следовательно, лишь тремя параметрами: углами поворота плоскостей нитрогрупп относительно плоскости бензольного кольца вокруг связей С-N. Кристаллическая структура в целом определяется девятью параметрами: координатами х, у, z центра бензольного кольца в ячейке, его эйлеровыми углами φ, ψ, χ и упомянутыми углами поворота δ₁, δ₂ и δ₃. В начале процесса минимизации последние можно даже не варьировать, задав их равными нулю, и лишь после достижения достаточно низ-кого уровня по Φ присоединить к остальным шести переменным.

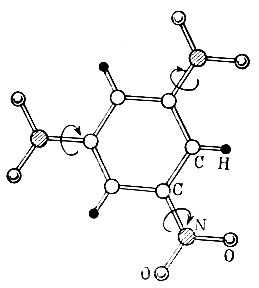
Рис. 56. Молекула 1, 3, 5 - тринитробензола

Правильность движения к глобальному минимуму Рис. 56. Молекула 1,3,5- следует контролировать не тринитробензола только по понижению функционала Φ (или уменьшению R-фактора), но с определенными интервалами и па изменению (прояснению) характера получаемого распределения электронной плотности. Необходимость этого связана, в частности, с тем, что во многих случаях функционал Φ имеет несколько достаточно глубоких минимумов, из которых лишь один (естественно, самый глубокий) отвечает реальной структуре.

На первый взгляд, метод минимизации функционала менее перспективен, чем метод межатомной функции или статистический метод, поскольку требует априорного знания архитектуры отдельных фрагментов структуры. И действительно, при расшифровке структур средней сложности метод минимизации явно уступает и в общности подхода и в надежности двум другим и пользоваться им вряд ли целесообразно.

Следует, однако, обратить внимание на то, что и паттерсоновский, и статистический методы, взятые в отдельности, ограничены в своих возможностях структурами определенной степени сложности. С увеличением числа атомов N в элементарной ячейке число максимумов паттерсоновской ячейки N (N-1) становится настолько большим, что они начинают сливаться, и распределение Р(и, v, w) перестает быть информативным^*. Одновременно с ростом N уменьшается и среднее значение структурного произведения Х_H,H', поскольку уменьшаются значения долевых коэффициентов g_j^**. А это значит, что относительное число "слабых" структурных произведений Х_H,H' возрастает и убедительность статистического определения знаков (и тем более начальных фаз) отражений понижается.

^* ( Исключения составляют сложные структуры с относительно малым числом тяжелых атомов. Для фиксации координат тяжелых атомов метод межатомной функции незаменим независимо от общей сложности структуры.)

^** (Среднее 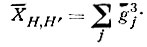. И так как долевые коэффициенты меньше единицы и уменьшаются при увеличении числа атомов (поскольку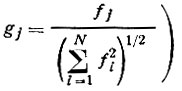, то 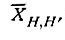также уменьшается с возрастанием N и притом довольно быстро)

Между тем метод минимизации структурного функционала можно применять к все более сложным структурам определенных химических классов, коль скоро результаты предшествующих структурных исследований дают основу для конструирования деталей строения молекул более сложного состава. В этом методе неизвестными являются лишь те параметры, которые добавляются при исследовании каждой новой структуры в ряду химически родственных соединений. Поэтому в принципе метод минимизации не ограничен рамками структур определенной сложности. В этом его преимущество.

В целом же в отношении сложных структур, не поддающихся расшифровке стандартными приемами, наиболее надежен, повидимому, путь комбинированного применения различных методов анализа. Для фиксации координат тяжелых атомов используется паттерсоновское распределение. Учет вклада тяжелых атомов в структурные амплитуды может усилить действенность статистического метода оценки начальных фаз этих амплитуд. Априорные данные о строении отдельных фрагментов могут, с одной стороны, облегчить более глубокий анализ паттерсоновского распределения, с другой - включить в общую схему анализа минимизацию структурного функционала. Словом, способов комбинирования трех основных методов расшифровки и различных специальных приемов, созданных на их основе, может быть очень много. С накоплением опыта, вероятно, выкристаллизуются определенные схемы и комбинации приемов анализа сложных структур (адекватные уровню развития вычислительной техники). Об этом, в частности, свидетельствует становление приемов структурного анализа в такой специфической области, как химия белков. Здесь широко используется метод фиксации позиции тяжелых атомов, специально вводимых в белок, сравнение паттерсоновских распределений для ряда изоструктурных производных белка, выявление знаков (начальных фаз) структурных амплитуд путем статистической обработки данных о разности единичных амплитуд в изоструктурных парах (метод изоморфного замещения). На определенной стадии анализа привлекаются и априорные сведения о геометрическом строении отдельных группировок, входящих в состав белка^*.

^* (Более детальную характеристику специфических методов структурного анализа белков см. в кн.: Бландела Т., Джонсон Л. Кристаллохимия белка. М., Мир, 1979.)