§ 10. Уточнение координатных и других параметров структуры

После выявления всех атомов в процессе последовательного очищения распределения электронной плотности исследователь переходит к уточнению координат атомов с учетом различных побочных факторов, влияющих на интенсивность дифракционных лучей. Обычно уточнение проводится классическим методом наименьших квадратов (МНК).

Основу составляет все тот же лишь слегка видоизмененный структурный функционал

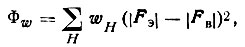(70)

где |F_э| -сокращенная запись |F(hkl)|_эксп, |F_в|-аналогичная запись |F (hkl)|Н означает h, k, l. Весовые множители w_H предполагаются пропорциональными точности измерения интенсивности соответствующих отражений.

Обозначим координаты x_j, y_j, z_j всех n независимых атомов ячейки, а также другие возможные параметры, влияющие на F(hkl)_выч, одним и тем же символом где i=1, 2,..., 3n,…q,

Задача заключается в нахождении значений ξ_i отвечающих минимуму функционала Φ, т. е. в решении системы уравнений

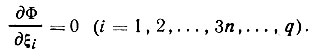(71)

Поскольку искомые параметры входят в F(hkl)_выч, система приводится к виду д IF I

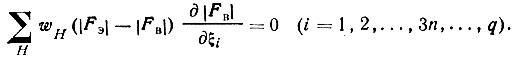(72)

В общем виде система не решается, так как искомые координатные параметры находятся в аргументах тригонометрических функций, из которых построены F (hkl)_выч^*. Можно, однако, воспользоваться тем, что приближенное решение структуры уже найдено, следовательно, известны значения ξ_i⁰, достаточно близкие к искомым ξ_i. Поэтому, разложив |F(hkl) _выч| в ряд Тейлора, можно оборвать его на втором члене:

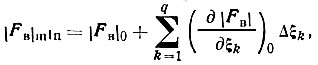(73)

где 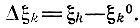. Такое приближение означает, что в пределах изменения параметров функция |F_в| меняется линейно и, следовательно,

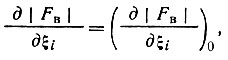
где 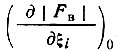значение производной при параметрах ξ⁰_i. Подставив (73) в (72) и учтя (74), получим

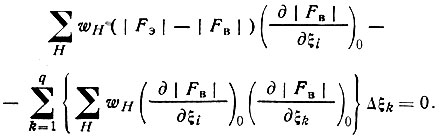(75)

Обозначив

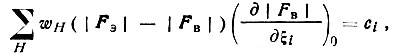(76)

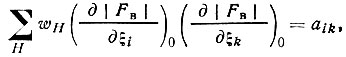(77)

получим систему из q линейных уравнении^** вида я

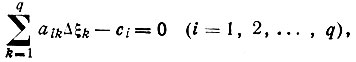(78)

что позволяет найти значения всех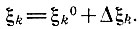

^* (Именно поэтому в методе минимизации структурного функционала приходится идти наощупь, анализируя направление градиента при каждом шаге движения к минимуму.)

^** (В матричной записи 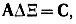, где А - матрица нормальных уравнений 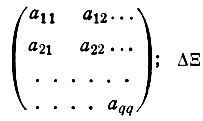; Δ Ξ - определяемый вектор 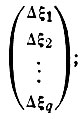; С - вектор правых частей .)

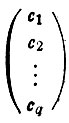Естественно, что обрыв ряда Тейлора на первых членах, а также изменение начальных фаз отражений при уточнении координат заставляют повторять уточнение несколько раз, т. е. делают процесс итерационным. Поскольку, однако, мы имеем дело с чисто математической процедурой, весь этот процесс может быть полностью автоматизирован.

Помимо первых 3n параметров ξ_i отвечающих координатам х_j, y_j, z_j, обычно уточняются константы тепловых колебаний атомов и константа приведения |F(hkl)_эксп. К абсолютной шкале - к тем же электронным единицам, в которых рассчитывается |F(hkl)|_выч.

Тепловые колебания атомов "размазывают" усредненную по времени электронную плотность атомов, что видоизменяет атомные кривые f sin θ/λ (рис. 57). Соответствующие поправки к f_i имеют вид

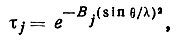(79)

если тепловые колебания изотропны, и

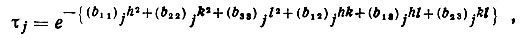(80)

если колебания анизотропны.

Эти поправки входят в состав | F(hkl) |_выч как множители при f_i:

(81)

Уточняемыми параметрами служат константы (b_rs)_j (всего n констант) или константы (b_rs)_j (всего 6n констант).

Для учета константы приведения к абсолютной шкале (масштабного коэффициента К) в принципе следует заменить |F(hkl) |_эксп на K|F(hkl) |_эксп. Но для того чтобы все уточняемые параметры входили в одну и ту же функцию, минимизуется функционал

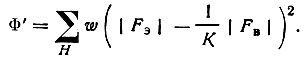(82)

Таким образом на каждом шаге итерации требуется составить квадратную матрицу коэффициентов a_ik и линейную c_i порядка 4n+1 в изотропном приближении и 9n+1 в анизотропном приближении.

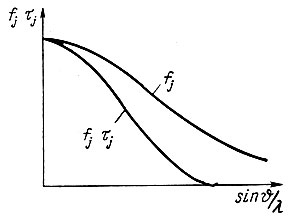
Рис. 57. Изменение кривой атомного рассеяния при введении температурной поправки

В прецизионных исследованиях помимо тепловых колебаний атомов учитывается (и уточняется) также ряд других побочных факторов, воздействующих на интенсивность дифракционных лучей, в частности, параметры эмпирической формулы, учитывающей вторичную экстинкцию (см. гл. IV, § 1).

При уточнении структуры средней сложности, скажем, содержащей 30 независимых атомов, с учетом анизотропии тепловых колебаний число уточняемых параметров превышает 270. Это означает, что на каждом шаге итерационного процесса требуется определить коэффициенты матрицы a_ij 270-го порядка, т. е. около 53 тыс. констант. Если же число независимых атомов приближается к сотне, то число коэффициентов a,sub>ij превышает уже 800 тыс. Поэтому при отсутствии сверхмощных ЭВМ приходится заботиться об упрощении расчетной процедуры и прибегать к приближениям диагональных и блок диагональных матриц. Основой такого упрощения служит то обстоятельство, что, как правило, диагональные члены матрицы А значительно больше недиагональных: a_ii>>a_ij с i≠j. Это и позволяет воспользоваться "диагональным" приближением, т. е. условно принять, что все недиагональные члены матрицы равны нулю. Естественно, что это несколько огрубляет результаты уточнения и, следовательно, увеличивает общее количество последовательных итераций.

Анализ физического смысла коэффициентов a_ij приводит к выводу, что условие a_ii>>a_ij с i≠j выполняется не всегда. Это относится прежде всего к тем i и j, которые отвечают трем координатам х, у, z или к шести константам тепловых колебаний одного и того же атома. То же может относиться и к параметрам атомов, образующих тесную жесткую группу, например к атомам бензольного кольца (ибо смещение одного из них вызывает, естественно, и смещения всех остальных атомов кольца). Здесь также не рекомендуется пренебрегать недиагональными членами матрицы А. Все это приводит к промежуточному варианту расчета (промежуточному и по трудоемкости и по точности результата) - к "блок- диагональному" приближению расчета матрицы А. Схематически такую матрицу можно представить в виде

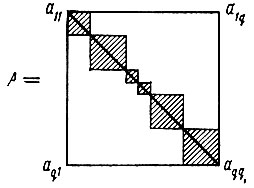
Коэффициенты a_ij, попадающие в не заштрихованные области, считаются равными нулю.

Следует, впрочем, помнить, что блок-диагональная схема не гарантирует близость к нулю всех неучтенных недиагональных элементов матрицы a_ij, т. е. отсутствие корреляции между параметрами, включенными в разные блоки. Если такая (незамеченная) корреляция имеется, то уточнение может оказаться иллюзорным: значения коэффициентов a_ij одного блока могут измениться за счет коэффициентов другого блока, а не за счет приближения к "истине". Простейшим примером может служить корреляция между константой приведения к абсолютной шкале К и усредненной по всем атомам константой В тепловых колебаний. Если обе эти поправки рассматривать как единичные матрицы, то они неизбежно будут искажать друг друга, так как обе монотонно (хотя и по разному закону) изменяют амплитуды всех отражений, т. е. действуют на весь массив отражений более или менее одинаково. Обе эти константы следует всегда включать в один блок.

Выше (гл. II, § 7) уже отмечалось, что для уточнения структурных параметров можно использовать и данные порошковой дифрактометрии (особенно при полно профильном анализе дифрактограммы). Этот метод имеет и некоторые преимущества перед монокристальным: точнее (и проще) учитывается поглощение лучей в исследуемом образце, исчезает необходимость вводить поправку на экстинкцию. Однако возможности и точность полнопрофильного анализа порошковой дифрактограммы тем ниже, чем сложнее структура (чем больше наложений линий на дифрактограмме). Поэтому этот метод наиболее перспективен для сильно поглощающих соединений с не слишком большими параметрами решетки (а также, естественно, для веществ, не дающих монокристаллов вообще, при условии, что их атомное строение в принципе известно на основе изоструктурности).