§ 11. Обработка результатов исследования

Основная задача почти каждого структурного исследования заключается в выявлении общего структурного мотива взаимного расположения атомов и в определении конфигурации отдельных фрагментов структуры - молекул, молекулярных ионов, координационных полиэдров и др.

Составной частью описания структурного мотива и строения фрагментов структуры является их графическое изображение. Как, правило, используются три способа изображения: 1) в виде проекций элементарной ячейки (или ее независимой области) на одну или несколько координатных плоскостей (рис. 58, а); в виде рисунка модели интересующего исследователя фрагмента (рис. 58, б), часто с изображением вместо атомов эллипсоидов их тепловых колебаний (рис. 58, в); 3) в виде стереоскопической пары, изображающей ячейку или ее фрагмент в двух слегка различных проекциях, что позволяет отчетливо видеть детали пространственного размещения атомов при помощи простейшего стереоскопа (рис. 58, г).

Помимо качественного описания результатов, существенны также и различные количественные характеристики геометрии фрагментов структуры. К таковым относятся, в первую очередь, межатомные расстояния и валентные углы.

Рис. 58. Способы изображения результатов структурного анализа: а - проекция элементарной ячейки транс-Pt(NH₃)2Cl₂; б - изображение молекул NifPPhshCh; в - фрагмент структуры с эллипсоидами тепловых колебаний атомов (ион [MeSe(AlMe₃)₃]); г - стереоскопическая пара изображения молекулы 2-бром-3,3,5,5-тетраметилциклогексана

Расчетные формулы последних выводят на основе общих соотношений аналитической геометрии и тригонометрии. Вектор, связывающий два атома с координатами x₁, y₁, z₁ и x₂, y₂, z₂, определяется как

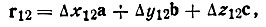
где 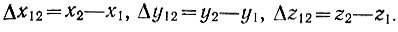. Отсюда получим

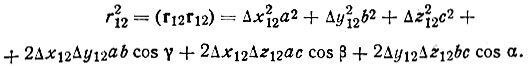(83)

Валентный угол между векторами r₁₂ и r₁₃ определяется решением треугольника:

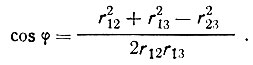(84)

Из других количественных характеристик чаще всего приходится иметь дело с установлением значений отклонения атомов некоторого фрагмента от общей плоскости. Задача ставится следующим образом: требуется найти плоскость, которая в среднем отклонялась бы минимально от заданной совокупности точек. Решается она методом наименьших квадратов. Пусть искомая плоскость определяется уравнением

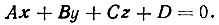
Положение атомов задается их координатами x_i, y_i, z_i. Некоторый i-й атом отклоняется от плоскости на величину

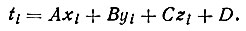(85)

Составим функционал 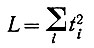и будем искать параметры А, В, С, D плоскости, делающей этот функционал минимальным. Требуется, следовательно, приравнять нулю четыре частные производные L по А, В, С и D и решить полученную систему уравнений относительно этих параметров. После этого соотношение (85) позволяет найти отклонение от плоскости любого атома (как из совокупности, взятой за основу, так и любого другого атома).

В конкретных структурных исследованиях возникают и другие частные геометрические задачи, рассматривать которые мы здесь не будем.

Важным вопросом, возникающим при обработке результатов, является оценка их точности. В качестве общей, в известной степени условной характеристики точности структурного анализа используется фактор расходимости, даваемый формулой (43).

Обычно считается, что структура с заключительным значением R-фактора на уровне 0,2 определена с низкой точностью: значению R≅0,08 отвечает средняя точность: при R≅0,05/0,04 структура определена с хорошей точностью, при R≤0,2 - прецизионно^*.

^* (Условность этого критерия видна из следующего обстоятельства. Точность определения координат тем ниже, чем меньше отражений используется для их определения. Но R-фактор при значительном сокращении числа отражений не возрастает, а уменьшается. Ведь в пределе, когда число отражений берется равным числу определяемых параметров, он должен автоматически сводиться к нулю.)

Несколько иной смысл имеет другая общая характеристика результата структурного исследования, так называемый показатель добротности S, определяемый формулой

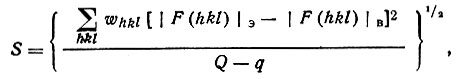(86)

где Q - общее число отражений, использованных при уточнении структуры, a q - число уточняемых параметров. Смысл этого показателя заключается в следующем. Весовые множители w_hkl обратно пропорциональны квадратам вероятных погрешностей в измерении |F(hkl)_э| соответствующих отражений σ(|F(khl) |_э). Поэтому члены суммы, стоящей в числителе, w_hkl[|F (hkl)|_э - |F(hkl) |_в]² в принципе должны варьировать вокруг значения, равного единице, а сумма по всем отражениям Q, деленная на Q - q, должна быть немного больше единицы. Если показатель добротности значительно превышает единицу, то это свидетельствует либо о заниженной оценке вероятных погрешностей (которые рассчитываются по определенным формулам для случайных ошибок), либо о наличии в эксперименте незамеченных систематических ошибок, увеличивающих разности |F(hkl)|_э-|F(hkl)|_в

Существенны, однако, не только (и не столько) эти общие характеристики, но значения вероятной погрешности определения каждого из параметров структуры: координат атомов, констант тепловых колебаний, межатомных расстояний и валентных углов.

Имеется два основных источника погрешностей. Первый- ошибки (случайные и систематические), вносимые при оценке интенсивности отражений и при их первичной обработке [при переходе от I (hkl) к |F(hkl)|_эксп, требующей учета ряда побочных факторов. Второй - ошибки той модели, которая используется при конструировании F(khl)_выч; в частности, имеется в виду использование стандартных и изотропных значений атомных амплитуд f_j и гармонического приближения фактора тепловых колебаний τ_j.

Поскольку ошибки первого типа сказываются на |F(hkl)|_эксп, а второго на F(hkl)_выч, принято считать, что в хорошем приближении погрешность, вносимая в общий результат отдельной структурной амплитудой, пропорциональна разности | F(hkl) | _эксп- | F (hkl) | _выч. На этой основе и конструируются формулы вероятных погрешностей в координатах атомов. В соответствии с общей теорией вероятных погрешностей для стандартных отклонений (вероятных погрешностей) в параметрах, получаемых по МНК, имеем

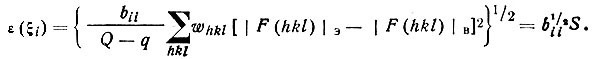(87)

Здесь b_ii - диагональный элемент матрицы В, обратной матрице нормальных уравнений А (см. § 10), т. е.

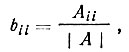(88)

где |A| -детерминант, составленный из коэффициентов a_ik, а A_ii и - его "алгебраическое дополнение", т. е. детерминант, полученный вычеркиванием i-й строки и i-го столбца.

Стандартные отклонения в расстояниях и углах определяются по стандартным отклонениям в координатах в соответствии с обычными формулами теории вероятных погрешностей.

Вероятная погрешность в расстоянии между атомами и 2 с координатами x₁,y₁, z₁ и x₂, y₂, z₂

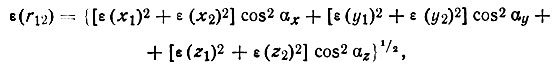(89)

α_x, α_y, α_z - направляющие углы вектора r₁₂.

Вероятные погрешности в значении угла между векторами r₁₂ и r₁₃, приведенными из атома 1 в атомы 2 и 3,

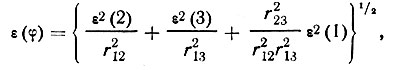(90)

где ε(1), ε(2) и ε(3) -среднеквадратичные (по трем координатам) стандартные отклонения в позициях атомов 1, 2 и 3.

Следует напомнить, что стандартное отклонение (дисперсия) по своему физическому смыслу - лишь доверительный предел. О реальности различия двух расстояний r₁₂ и ₃₄, отличающихся на ε (r), можно говорить лишь с 68,3-процентной вероятностью. Если разница достигает 1,96ε, вероятность того, что она реальна, возрастает до 95%; при разнице в 2,58ε - до 99%. В структурных исследованиях принято вообще не обсуждать физического смысла тех различий в параметрах, которые лежат в пределах стандартных отклонений. Различия, достигающие удвоенной вероятной погрешности, обсуждаются лишь в определенных условиях, например, когда они подтверждаются аналогичными различиями в других родственных структурах или другими стереохимическими закономерностями. Различия, превышающие утроенную погрешность, считаются реальными всегда. Если же полученное различие представляется физически невероятным, делается оговорка о занижении оценки погрешности всех параметров при использовании общих формул в данных конкретных условиях.