Анализ тепловых колебаний атомов в кристалле

Константы изотропных тепловых колебаний B_j или анизотропных колебаний (b_rs)_j, входящие в выражение для температурного фактора τ_j при атомных амплитудах, имеют физический смысл среднеквадратических значений амплитуд тепловых колебаний атомов. При относительно низкой точности эксперимента и недостаточно высоком уровне учета побочных факторов такое содержание констант B_j и (b_rs)_j остается лишь номинальным. Фактически же они аккумулируют основную долю систематических погрешностей измерения и обработки интенсивности отражений, освобождая от этих погрешностей те компоненты структурных амплитуд, которыми определяются координаты атомов. При повышении точности эксперимента и обработки данных физическое содержание B_j и (b_rs)_j восстанавливается. Их определение становится задачей исследования.

Уже чисто качественное сопоставление преимущественных направлений колебаний атомов в молекуле, комплексе или любом другом фрагменте кристалла представляет вполне определенный интерес для физико-химиков. Сопоставление ориентации эллипсоида тепловых колебаний атома с направлениями его связей с соседями позволяет судить об относительной прочности этих связей и об их влиянии на характер колебаний атома.

В структурном анализе тепловые колебания атомов рассматриваются как полностью независимые, что, вообще говоря, неправильно. Поэтому при более детальном количественном анализе структурных данных требуется прежде всего отделить групповые колебания атомов от их индивидуальных колебаний.

Эта проблема касается прежде всего кристаллов молекулярных и комплексных соединений; речь идет о разделении колебаний молекулы (комплекса) как целого и колебаний атомов внутри молекулы. Математический аппарат этого разделения уже создан и расчет констант трансляционных и либрационных колебаний молекул в кристаллах уже можно включать в заключительную обработку результатов структурного исследования как ее составную часть.

Следующий шаг состоит в установлении корреляции между данными о тепловых колебаниях, полученными в ходе структурного анализа, и аналогичными сведениями, даваемыми ИК-спектроскопией.

Необходимо, впрочем, отметить, что для решения вопросов, связанных с тепловыми колебаниями, нейтронография более перспективна, чем РСА. При рассеянии рентгеновских лучей тепловые колебания выступают как фактор, "размазывающий" электронную плотность атомов, и остается не до конца ясным, какая доля этого размазывания определяется колебаниями, а какая - перераспределением электронной плотности при переходе от изолированных атомов к атомам в кристалле. В нейтронографии же фиксируются непосредственно тепловые колебания ядер, так как ядра сами по себе не размыты.

Следующий, более глубокий, этап в изучении тепловых колебаний атомов, к которому уже обращаются при наиболее прецизионных исследованиях, заключается в учете ангармонизма тепловых колебаний. Формула (80), содержащая шесть констант b_sj для каждого атома, предполагает, что колебания атомов носят гармонический характер, т. е. что распределение средних амплитуд колебаний по разным направлениям может быть описано эллипсоидом. Реальная ситуация в химических соединениях не такова. Например, ковалентное взаимодействие между атомами при не центросимметричном (например, тетраэдрическом) распределении направлений связывания явно нарушает симметрию тепловых колебаний вдоль связей (к соседнему атому и от соседнего атома). При исследовании кристаллов (в том числе ионных и интерметаллических) при температурах, приближающихся к точке фазового перехода, резко возрастают тепловые колебания атомов в тех особых направлениях, в которые они необратимо смещаются после фазового перехода. Во всех таких и многих других случаях гармоническое приближение становится недостаточным для изучения физики явления. Если гармонические колебания определяются тензорами второго ранга 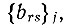, то для анализа энгармонизма приходится иметь дело с тензорами третьего ранга 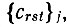, тензорами четвертого ранга 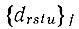и т. д. с соответствующим быстрым увеличением числа параметров, характеризующих ангармонизм количественно. В общем случае асимметричного кристалла (точечная группа C₁=1) тензор третьего ранга содержит 10 независимых констант, тензор четвертого ранга- 15 независимых констант^*. При учете ангармонизма колебаний температурный фактор можно записать в виде

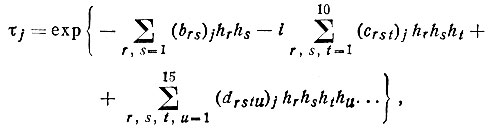(91)

где h_r, h_s и т. д. - любой из индексов h, k, l [ср. с формулой (80)].

Увеличение числа параметров, уточняемых в процессе МНК, требует адекватного увеличения числа экспериментальных |F(hkl)| и повышения их точности. Поэтому такие задачи можно решать только при очень прецизионных исследованиях и на основе большого массива экспериментальных данных.

^* (Все тензоры симметричны к любой перестановке индексов.)