Глава 3. Атом водорода

В этой главе рассматриваются решения уравнения Шредингера для простейшего атома. Эти решения приводят к понятию атомной орбитали, которое является фундаментальным в современной теории валентности.

Атом водорода состоит из электрона и протона, которые притягиваются друг к другу по закону Кулона. Если r - расстояние между этими частицами, то их потенциальная энергия равна

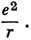
Именно эту потенциальную энергию и надо включить в уравнение Шредингера (1.12). Поскольку протон значительно тяжелее электрона, можно упростить задачу и при рассмотрении движения электрона считать, что протон покоится и находится в центре масс. Тогда уравнение Шредингера для электрона запишется в виде ^*)

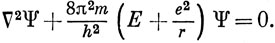
^*) (В действительности протон не является центром масс, и чтобы это учесть, m в соотношении (3.1) надо заменить так называемой приведенной массой протона и электрона

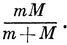
Так как масса протона значительно больше массы электрона, приведенная масса очень близка к m.)

Если потенциальное поле обладает сферической симметрией, как это имеет место в рассматриваемой задаче, уравнение Шредингера проще решать в сферических, а не в декартовых координатах. На рис. 3.1 показаны сферические координаты: r - расстояние до электрона от протона; θ - угол, образуемый r с осью z; φ - угол, который образует с осью х проекция вектора r на плоскость xy. Декартовы и сферические координаты связаны следующими соотношениями:

Область изменения сферических координат: 0 ≤ r ≤ ∞, 0 ≤ θ ≤ π, 0 ≤ φ ≤ 2π. Дифференцируя уравнение (3.2), можно показать, что элементы объема в этих системах координат связаны соотношением

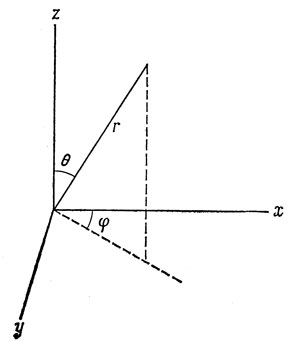
Рис. 3.1. Сферические координаты

В сферических координатах уравнение Шредингера выглядит более громоздко, чем выражение (3.1):

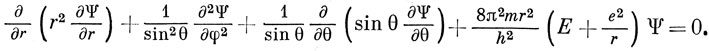
Однако хорошо известно, что решения любой задачи, содержащей сферически симметричный потенциал, можно представить в виде произведения радиальной функции на функцию, зависящую от угловых переменных ^*).

Радиальную функцию R(r) рассмотрим позднее.

^*) (Поскольку в выражении (3.4) отдельные слагаемые зависят только от r или угловых переменных θ и φ, переменные в нем разделяются. Таким образом, решение его имеет вид соотношения (3.5), где функции r и угловых переменных θ, φ являются решениями соответствующих дифференциальных уравнений.)

Функции Υ_lm называются сферическими гармониками и удовлетворяют дифференциальному уравнению

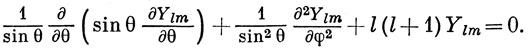
Для сферических гармоник выполнены периодические граничные условия, которые налагаются требованием неизменности волновой функции Ψ при замене θ на θ + 2π и φ на φ + 2π. Сферические гармоники нумеруются целыми числами l и m, причем

и для данного l число m может иметь 2l + 1 различных значений:

Квантовые числа l и m, как показано в гл. 8, связаны с орбитальным угловым моментом электрона ^*) (моментом импульса).

^*) (l и m известны как азимутальное и магнитное квантовые числа соответственно по аналогии с квантовыми числами, появляющимися в теории Бора. В этой книге мы будем называть их квантовыми числами углового момента.)

Решения уравнения (3.4), имеющие вид (3.5), называются атомными орбиталями (АО). Когда говорят, что электрон занимает атомную орбиталь, то подразумевают, что он описывается волновой функцией, которая является решением соответствующего уравнения Шредингера.

Атомные орбитали в соответствии со значением l обозначаются следующим образом:

Первые четыре значка имеют историческое происхождение, так как связаны с характером спектральных линий: s, p, d, f - первые буквы английских слов sharp (резкий), principal (главный), diffuse (диффузный), fundamental (основной). Для наших целей наиболее важны следующие сферические гармоники:

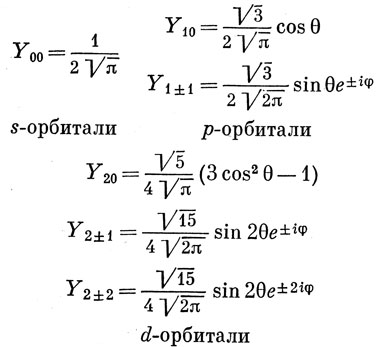
Заметим, что квантовые числа m входят в показатели экспоненциальных функций. Эти функции, будучи комплексными, имеют тот недостаток, что их невозможно изобразить в действительном пространстве. Однако можно получить действительные функции, являющиеся также решениями уравнения (3.4), используя линейные комбинации сферических гармоник с одним и тем же значением l (это будет доказано в гл. 6). Действуя таким образом, можно получить, например,

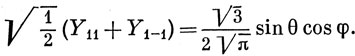
Поскольку sin θ cos φ выражает угловую зависимость x-компоненты радиуса-вектора r [см. выражение (3.2)], линейная комбинация (3.10) называется угловой частью p_x-атомной орбитали. Наиболее употребительные действительные функции, описывающие угловую зависимость s-, р- и d-атомных орбиталей, приведены в табл. 3.1. Полные волновые функции (атомные орбитали) получаются умножением этих функций угловых переменных на соответствующие радиальные функции R(r).

Таблица 3.1. Угловая зависимость атомных орбиталей

Подставляя волновую функцию в общем виде (3.5) в уравнение (3.4) и используя уравнение (3.6) для сферических гармоник, получим уравнение, определяющее радиальную функцию:

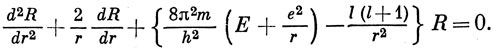
Имеется еще одно ограничение, налагаемое на решения этого уравнения: при r → ∞ они должны стремиться к нулю. В противном случае электрон не будет связан с ядром. Решения уравнения (3.11), удовлетворяющие этому граничному условию, можно записать в следующей форме ^*):

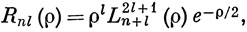
где

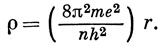
L_n+l^2l+1 - известные полиномы, называемые присоединенными полиномами Лагерра, которые являются решением дифференциального уравнения

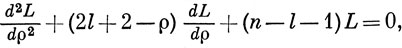
причем n - l - 1 должно быть положительным целым числом или нулем. Поскольку l - целые числа, то

^*) (Подробности решения уравнения (3.11) можно найти почти в любом курсе квантовой механики; например, в книгах [65] (гл. 5) и [24] (гл. 4 и 6).)

Число n называется главным квантовым числом. Таким образом, в решениях задачи об атоме водорода появляются три квантовых числа: n - из граничного условия для функции переменной r; l и m - из условий периодичности функции переменных θ и φ; ρ - безразмерная величина. Из констант, входящих в выражение (3.13), составим характерную длину

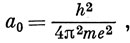
которая называется боровским радиусом, так как она равна радиусу орбиты, соответствующей наиболее низкой энергии в боровской теории атома водорода. Эта величина является единицей длины в так называемой атомной системе единиц; в этой системе за единицу приняты масса электрона и заряд протона и единица действия, равная

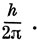
Тогда уравнение Шредингера для электрона в атомных единицах можно записать в виде

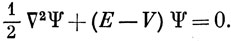
Решения уравнения (3.12) можно обобщить на случай водородоподобных ионов, таких, как Не⁺, Li²⁺, если заменить

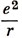
на

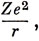
где Z - заряд ядра. Тогда ρ определяется по формуле

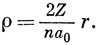
Радиальные функции для основных состояний этих одноэлектронных ионов приведены в табл. 3.2.

Таблица 3.2. Радиальные волновые функции R_nl(ρ) одноэлектронных атомов; все функции следует умножить на

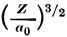
Уравнение (3.11), определяющее радиальную часть волновой функции и орбитальную энергию Е, содержит квантовое число l и не содержит квантового числа m. Поэтому энергия орбитали не зависит от m, откуда следует, что s-орбитали не вырождены, р-орбитали вырождены трехкратно, d-орбитали - пятикратно и т. д. С другой стороны, можно ожидать, что энергия Е будет зависеть от l. В случае атома водорода и водородоподобных ионов, для которых потенциальная энергия электрона равна

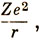
уровни энергии определяются формулой

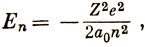
или в атомных единицах

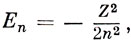
т. е. энергия зависит только от главного квантового числа n, причем уровни Е_n отрицательны и отсчитываются от энергии, соответствующей разведенным на бесконечное расстояние электрону и ядру.

Существуют также решения уравнения (3.11), для которых энергия Е положительна. Они соответствуют случаю, когда электрон не связан с ядром и волновые функции не обязаны удовлетворять граничному условию, согласно которому Ψ → 0 при r → ∞. Поэтому такие уровни энергии образуют континуум (ср. с задачей 2.1 о частице в свободном пространстве). Эти несвязанные состояния атома водорода не имеют отношения к теории валентности, поэтому в дальнейшем они не рассматриваются.

Если электрон переходит с орбитали с главным квантовым числом n₁ на орбиталь с главным квантовым числом n₂, то этот переход сопровождается поглощением или излучением света, так чтобы выполнялся закон сохранения энергии. Из соотношения (3.19) следует, что

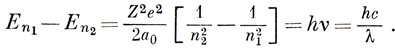
Этот результат находится в согласии с формулой Ритца (1.4), а значение постоянной Ридберга такое же, как и в теории Бора [см. выражение (1.5)].

В обозначении атомной орбитали указывается не только угловая зависимость соответствующей волновой функции (см. табл. 3.1), но также и ее главное квантовое число. Речь идет, например, об 1s-, 2s-, 2p-, 3s-, 3р-, 3d-орбиталях и т. д. Заметим, что 1p-, 1d- или 2d-орбитали не существуют в силу ограничения (3.15). Орбитали с n = 1 называют K-оболочкой, с n = 2 - L-оболочкой, с n = 3 - М-оболочкой и т. д.

Полные волновые функции одноэлектронных атомов приведены в табл. 3.3.

Таблица 3.3. Нормированные атомные орбитали одноэлектронных атомов

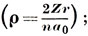
все функции следует умножить на

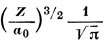
Рассмотрим сначала 1s-орбиталь атома водорода. Она сферически симметрична и убывает экспоненциально с расстоянием от ядра. График функции Ψ_1s(r) представлен на рис. 3.2. Плотность вероятности для электрона, находящегося на этой орбитали, есть Ψ². Вероятность обнаружения электрона на расстоянии r от ядра получается перемножением плотности вероятности на площадь сферы радиуса r: 2πr²Ψ². Эта функция наряду с Ψ² также показана на рис. 3.2.

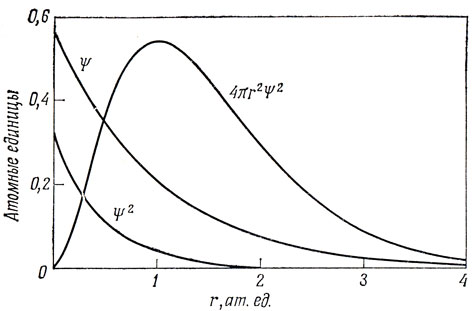
Pис. 3.2. Волновые функции и плотности вероятности для состояния с наименьшей энергией (1s) атома водорода

На рис. 3.2 представлена зависимость волновой функции Ψ и вероятности от расстояния r. Есть и другие способы графического толкования этих функций. Например, Ψ можно изображать посредством граничных поверхностей, которые представляют собой концентрические сферы; в сечении их плоскостью, проходящей через ядро, образуются концентрические окружности, изображенные на рис. 3.3, а. Можно также изобразить сферическую граничную поверхность, такую, что почти весь электронный заряд (например, 90%) находится внутри этой поверхности. На плоскости этому соответствует диаграмма 3.3, б. Наконец, можно представить плотность вероятности с помощью облака, густота которого уменьшается экспоненциально по мере удаления от ядра, как это показано на рис. 3.3, в.

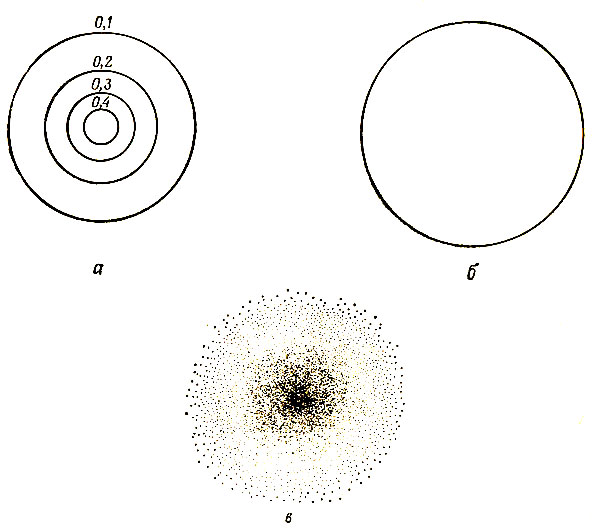
Рис. 3.3. Различные способы представления 1s-орбитали водорода. а - контуры; б - граничная поверхность; в - облако вероятности

Пространственное представление орбиталей с более высокими значениями n и l становится все труднее с ростом квантовых чисел. Начнем с графического изображения радиальной и угловой зависимостей в отдельности. Радиальные функции, приведенные в табл. 3.2, представлены на рис. 3.4. Отметим несколько важных свойств.

1. Размеры орбиталей увеличиваются с ростом n. Это непосредственно не видно из рисунка, поскольку по оси абсцисс отложено ρ, а не r.

2. Только s-орбитали имеют отличную от нуля плотность в ядре. Это важно иметь в виду при рассмотрении взаимодействия электронного и ядерного спинов, которое обнаруживается в явлении магнитного резонанса.

3. Функция обращается в нуль (т. е. имеет узел) n - l - 1 раз между 0 и ∞.

4. Среди орбиталей с одним и тем же n наибольшую электронную плотность вблизи ядра имеют те, у которых l меньше, причем главный максимум тем дальше от ядра, чем меньше l.

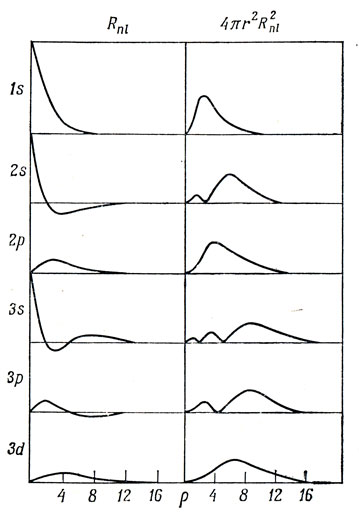
Рис. 3.4. Радиальные волновые функции и плотности вероятности для атомных орбиталей водорода

Угловые части функций, приведенные в табл. 3.1, представлены полярными диаграммами на рис. 3.5 и 3.6. Эти диаграммы строятся следующим образом: на радиусе-векторе выбирается точка, расстояние которой до начала координат равно модулю функции при значениях θ и φ, задаваемых этим радиусом-вектором. Такие точки определяют поверхности, изображенные на рис. 3.5. Сечения этих поверхностей плоскостью xz показаны на рис. 3.6. Знак угловой функции вдоль выделенного направления указан для каждого из объемов, охватываемых поверхностями.

Рис. 3.5. Полярные модели орбиталей. a - s; б - p; в - d_x²-y²; г - d_z²; д - d_xy (d_xz, d_yz)

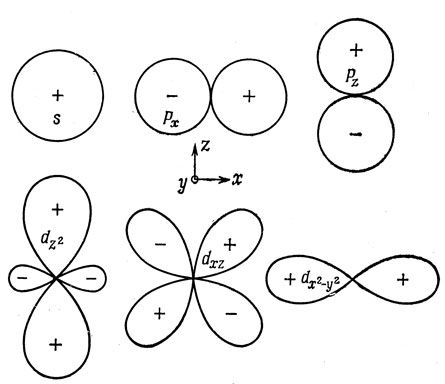
Рис. 3.6. Полярные диаграммы для s-, p- и d-орбиталей

s-Функция изображается сферой. Для других же функций существуют выделенные направления в пространстве, вдоль которых функции имеют наибольшее значение; эти направления играют важную роль в теории валентности. р-Функции представляются парами сфер, касающихся друг друга в начале координат; три p-функции имеют одинаковую форму, но они ориентированы вдоль различных координатных осей. d-Функции, кроме d_z², изображаются четырьмя грушевидными "лепестками"^*), направленными к углам квадрата. Орбитали d_z² имеют два больших по размеру грушевидных "лепестка", направленных вдоль оси z и опоясанных в центре кольцом.

^*) (Термин "лепестки", по нашему мнению, неудачен, так как речь идет о пространственной картине, но принят в русских переводах. - Прим. ред.)

Поскольку три p-орбитали отличаются только своей ориентацией в пространстве, из физических соображений ясно, что они должны иметь одинаковую энергию. Это обстоятельство уже отмечалось в связи с тем, что квантовое число m не содержится в радиальном уравнении. Так как d_z²-орбиталь отличается от остальных четырех d-орбиталей, сразу не очевидно, что пять d-орбиталей, по существу, эквивалентны. Под эквивалентностью подразумевается независимость любого измерения, выполненного для электрона, от того, на какой именно d-орбитали он находится (при условии, что три координатные оси в пространстве эквивалентны). Различие между d-орбиталями только кажущееся: d_z²-орбиталь может быть записана как линейная комбинация двух орбиталей, имеющих такую же форму, как и остальные четыре d-орбитали, а именно d_z²-x² и d_z²-y², но не являющихся независимыми (z² - х² + z² - у² = 3z² - r² есть функция с такой же угловой зависимостью, как и d_z²-орбиталь).

Полная волновая функция может быть теперь представлена комбинированием значений радиальной и угловой частей в соответствии с выражением (3.5). Она нагляднее всего изображается с помощью контурных диаграмм, как это сделано для p_z-орбитали на рис. 3.7. Однако очень удобным, хотя и приближенным, является представление орбиталей с помощью угловых частей, как показано на рис. 3.6. Оно будет неоднократно использовано на протяжении этой книги. Как видно, волновая функция может иметь положительную и отрицательную области. Однако наблюдаемые свойства электрона зависят не от функции Ψ, а от функции Ψ² (в более общем случае - от Ψ^*Ψ), которая всегда положительна. Какова же тогда роль знака и существен ли он вообще? Для выяснения этого проведем здесь аналогию с амплитудой световой волны. Она может быть положительной или отрицательной, но знак важен только в том случае, когда две волны интерферируют. Тогда соотношение знаков обеих амплитуд определяет, будет ли происходить при интерференции взаимное ослабление или усиление волн. Аналогично, как будет видно из теории химической связи, важно именно соотношение знаков двух перекрывающихся атомных орбиталей, а не знаки каждой из них в отдельности.

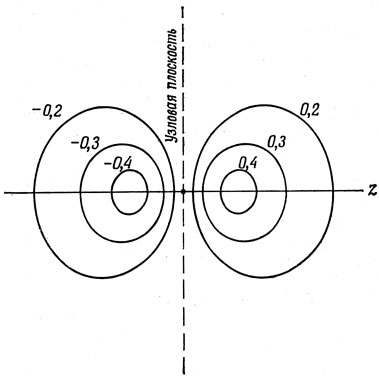
Рис. 3.7. Контуры р_z-орбитали в плоскости xz

Наконец, несколько слов относительно связи между решениями уравнения Шредингера для атома водорода и теорией Бора. Обе теории приводят к одному и тому же выражению для энергии, но с помощью волновых функций, получаемых из уравнения Шредингера, удается объяснить другие свойства электрона и прежде всего вычислить вероятности поглощения и излучения света, между тем как теория Бора не дает такой возможности. Квантовые числа появляются при решении уравнения Шредингера естественно благодаря граничным условиям, тогда как их приходится вводить в теорию Бора искусственно. Электроны, согласно теории Бора, занимают орбиты, подобные орбитам планет. В соответствии же с решениями уравнения Шредингера электроны заполняют делокализованные орбитали. Многочисленные экспериментальные данные (например, получаемые из дифракции рентгеновских лучей электронные плотности) показывают, что правильной является последняя картина.