Глава 4. Многоэлектронные атомы и периодическая система элементов

Электрон в атоме, содержащем несколько электронов, находится под действием потенциального поля ядра и поля, создаваемого другими электронами. Например, для выделенного значком 1 электрона будем иметь

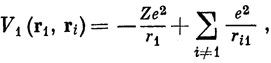
где r₁ - расстояние электрона 1 от ядра, r_i1 - расстояние между i-м электроном и электроном 1. С хорошей степенью приближения можно заменить V₁ потенциалом, в котором каждое слагаемое, выражающее отталкивание электронов, усреднено по координатам соответствующего электрона. Тогда потенциальная функция будет зависеть только от вектора r₁:

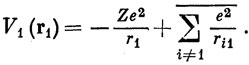
Вообще говоря, V(r₁) не имеет сферической симметрии, поскольку электроны i могут находиться на орбиталях, не обладающих такой симметрией (р, d и т. д.). Тогда приходится делать дальнейшее допущение, что V(r₁) можно усреднить по всем ориентациям в пространстве, чтобы получить потенциал центрального поля V(r₁). Подставляя этот усредненный потенциал в выражение (3.1) вместо e²/r, можно получить атомные орбитали в форме (3.5).

Этот способ сведения многоэлектронного уравнения Шредингера к виду (3.1) и методика решения уравнения были предложены Хартри и Фоком. Он известен как метод самосогласованного поля (ССП). Берется набор приближенных атомных орбиталей и вычисляется средний потенциал, действующий на каждый электрон. Эти потенциалы используются затем для расчета новых орбиталей, с помощью которых получаются лучшие приближения к усредненным потенциалам. Процедура повторяется до тех пор, пока набор орбиталей не даст те же потенциалы, с которыми он был получен. Математическое обоснование метода дано в гл. 10.

Атомные орбитали, полученные по методу ССП, приводятся или в виде таблицы (радиальная часть волновой функции табулируется для различных значений r), или же выражаются в аналитической форме, например,

где c_nζ - числа. Орбитали, полученные для многоэлектронных атомов, напоминают водородоподобные орбитали, и поэтому их удобно обозначать аналогичным образом: 1s, 2s, 2р и т. д. Однако главное квантовое число n имеет лишь тот смысл, что n - l - 1 есть число узлов радиальной функции между 0 и ∞ и не существует простой формулы для энергии, в которой n выступало бы как целое число, нумерующее уровни.

Значительное количество расчетов было выполнено с использованием весьма приближенных волновых функций типа (4.3), в которых используется только один член суммы. Наилучшие значения параметров n и ζ для орбиталей с главными квантовыми числами 1, 2 или 3 определяются следующими правилами Слэтера ^*):

1. n - главное квантовое число.

^*) (Эти правила получены на основе вариационной теоремы [на самом деле, правила Слэтера построены на чисто эмпирической основе; вариационные расчеты были проведены только для легких атомов. - Прим. ред.], рассмотренной в гл. 6.)

2.

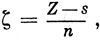
где Z - заряд ядра, a s (постоянная экранирования) учитывает экранирование ядра другими электронами в атоме.

3. Орбитали делятся на следующие группы: (1s); (2s, 2p); (3s, 3p); (3d) и т. д. Все орбитали одной группы имеют одну и ту же радиальную функцию.

4. Постоянная экранирования s вычисляется как сумма вкладов, вносимых отдельными электронами, по следующим правилам: а) электроны групп, находящихся снаружи от рассматриваемой группы, не вносят вклада в постоянную экранирования; б) вклад в s каждого электрона группы, к которой принадлежит рассматриваемый электрон, составляет 0,35; исключением является группа (1s), для которой эта величина берется равной 0,30; в) если рассматриваемый электрон относится к группе (s, p), каждый электрон внутренней группы с главным квантовым числом, меньшим на 1, увеличивает s на 0,85, а каждый электрон из более глубоких внутренних групп - на 1,00. Если электрон принадлежит к группе (d), то каждый электрон внутренних групп дает добавку к s, равную 1,00. Применим рассмотренные правила, например, к атому углерода: для 1s-орбитали s = 0,30, а для 2s- и 2р-орбиталей s = 3·0,35 + 2·0,85 = 2,75 соответственно. Следовательно, ζ_1s = 5,70; ζ_2s = ζ_2р = 1,625.

Для многоэлектронных атомов орбитали с одним и тем же значением n, но различными значениями l, не вырождены. При заданном n энергия увеличивается с ростом l. Это происходит потому, что с ростом l все меньшая часть волновой функции сосредоточена в области, близкой к ядру, так что усредненный экранирующий ядро заряд уменьшается. Это проиллюстрировано на рис. 4.1. Потенциал иона К⁺, вычисленный по методу ССП, представлен как функция r. Кроме того, показаны также радиальные электронные плотности 4π²r²R² для водородоподобных 3s-, 3р- и 3d-орбиталей (см. рис. 3.4). Очевидно, что электрон, занимающий 3s-орбиталь, находится в поле с наибольшим потенциалом и имеет поэтому самую низкую энергию; электрон же, находящийся на 3d-орбитали, испытывает действие наиболее слабого потенциала и имеет самую высокую энергию.

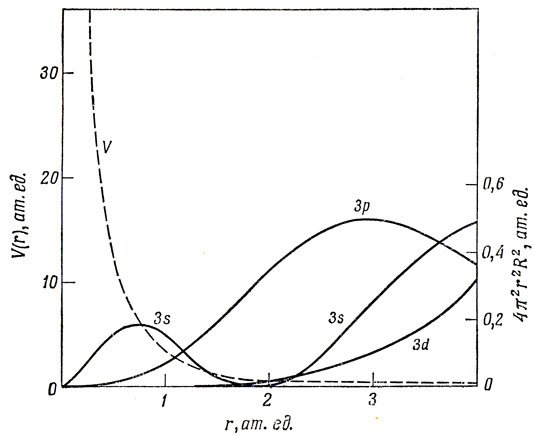
Pис. 4.1. Сопоставление потенциала иона К⁺ с водородоподобными 3s-, 3р- и 3d-орбиталями

Как будет сказано позднее, различия в энергии одно-электронных состояний с одним и тем же n, но разными l, играют важную роль в теориях строения атома и химической связи. С учетом дальнейшего, в табл. 4.1 приводятся приближенные значения разности энергий 2s- и 2p-орбиталей для атомов, расположенных во втором периоде системы элементов. Указанные величины являются лишь приближенными, поскольку энергия орбитали зависит также от того, в каких состояниях находятся остальные электроны атома.

Таблица 4.1. Приближенные значения разности энергий между 2s- и 2р-орбиталями (эв)

В 1925 г. Уленбек и Гоудсмит высказали предположение, что электрон представляет собой вращающуюся вокруг своей оси частицу и обладает поэтому спиновым угловым моментом и соответствующим ему магнитным моментом. Это позволило им объяснить некоторые особенности тонкой структуры атомных спектральных линий. При этом они постулировали, что спин квантуется во внешнем магнитном поле так, что проекция магнитного момента электрона на направление внешнего магнитного поля равна или + 1/2 (eh / 2mcπ) или - 1/2 (eh / 2mcπ). Результаты более ранних опытов Штерна и Герлаха (1922 г.) рассматривались как подтверждение этого постулата: в их опытах пучок атомов серебра пропускался через неоднородное магнитное поле, причем было обнаружено, что он расщепляется на два пучка, как если бы в пучке были атомы как с одним, так и с другим из двух возможных значений магнитного момента.

Спин электрона описывается квантовым числом s, которое может принимать значения + 1/2 или - 1/2 . Как видно из гл. 9, эти квантовые числа определяют проекцию спинового момента электрона в единицах h/2π.

Таким образом, для описания электронов имеются теперь четыре квантовых числа: n, l, m и s. В 1925 г. Паули сформулировал принцип исключения, согласно которому все четыре квантовых числа любых двух электронов в атоме не могут быть одинаковыми. Это означает, что орбиталь может быть занята или одним электроном со спином + 1/2 или - 1/2, или двумя электронами с противоположными спинами. Это ограничение, полностью исключающее возможность нахождения двух электронов с одинаковыми спинами на одной и той же орбитали, не имеет классического аналога.

В 1869 г. Менделеев указывал, что "физические и химические свойства элементов и их соединений представляют собой периодическую функцию атомного веса". Ему удалось предсказать свойства неизвестных тогда элементов (например, германия) с поразительной точностью. Если не считать замену атомного веса атомным номером как основы расположения элементов в таблице и включения новых элементов, то современная периодическая классификация элементов в основном та же, что и предложенная Менделеевым. Современная классификация элементов приводится в табл. 4.2. Атомный номер элементов увеличивается на единицу при переходе к следующему элементу, если таблицу читать обычным способом - слева направо.

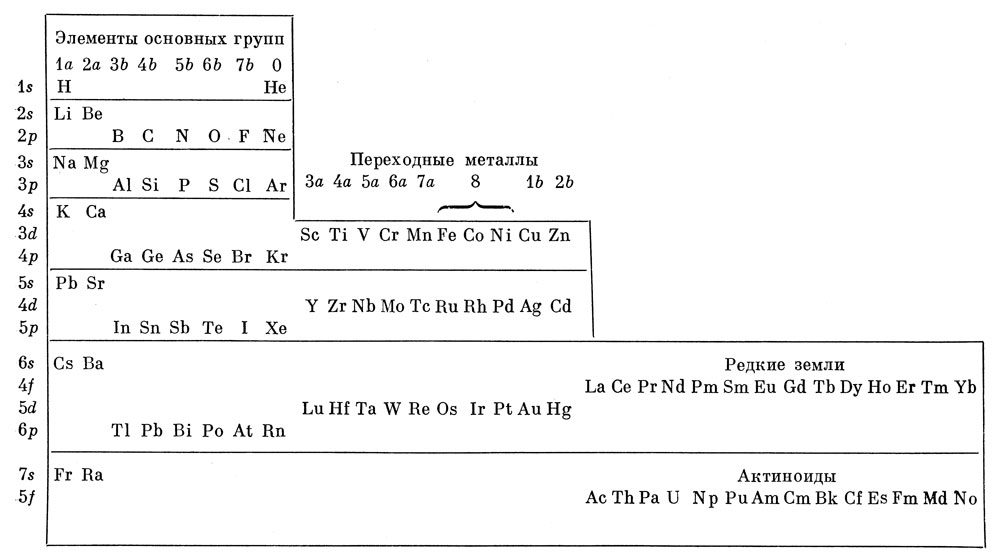
Таблица 4.2. Периодическая система элементов

Свойство периодичности элементов можно понять, рассматривая энергетические характеристики атомных орбиталей и учитывая принцип Паули. Это объяснение базируется на следующих правилах:

1. В основном состоянии атомов электроны занимают орбитали с наименьшей энергией, подчиняясь принципу Паули. Начиная с атома водорода, можно получить электронные конфигурации атомов других элементов, добавляя электроны по одному на атомные орбитали. Этот подход называется принципом построения.

2. np-Орбитали имеют более высокую энергию, чем ns-орбитали, но значительно более низкую энергию, чем (n + 1) s-орбитали.

3. nd-Орбитали обладают примерно такой же энергией, как (n + 1) s-орбитали, но более низкой, чем (n + 1) р-орбитали.

4. nf-Орбитали имеют приблизительно такую же энергию, как и (n + 1) d-орбитали.

На 1s-орбитали может находиться один электрон (атом водорода) или два электрона с противоположными спинами (атом гелия), которые образуют заполненную K-оболочку. Следующий добавляемый электрон надо поместить на 2s-орбиталь (атом лития). На 2s-орбитали может находиться еще один электрон (атом бериллия). Следующий электрон помещают на 2р-орбиталь (атом бора). Структуру атомов остальных элементов второго периода (от углерода до неона) можно получить, добавляя по одному электрону на 2р-подоболочку до тех пор, пока она не будет заполнена (всего в ней может быть шесть электронов). Тогда образуется заполненная L-оболочка в атоме неона, относящегося к так называемым инертным, или благородным, газам.

Одиннадцатый электрон помещают на 3s-орбиталь (атом натрия). Этот атом имеет один электрон вне заполненных оболочек подобно литию и всем другим элементам подгруппы 1а периодической системы. Этот внешний электрон определяет химические свойства атома, так что все элементы подгруппы 1а в химическом отношении весьма сходны.

Когда 3s- и 3р-подоболочки заполнены, следующий электрон добавляют на 4s-орбиталь (атом калия), а не на 3d-орбиталь. На основе спектроскопических данных можно видеть, что энергия 3d-орбитали атома калия примерно на 2,7 эв выше энергии 4s-орбитали. После заполнения 4s-орбитали начинается заполнение 3d-орбиталей; элементы с незаполненной d-подоболочкой называются переходными металлами. Для первого ряда переходных металлов различие энергий 4s- и 3d-орбиталей очень мало, так что в некоторых случаях 4s-орбиталь в основном состоянии атома не заполнена. Например, Сг имеет в основном состоянии конфигурацию (4s) (3d)⁵, а не (4s)² (3d)⁴; Cu - (4s) (3d)¹⁰, а не (4s)² (3d)⁹. Полностью или наполовину заполненные d-подоболочки приводят к дополнительной стабильности.

После заполнения 3d-подоболочки начинается заполнение 4р-подоболочки: образуются элементы от Gа до Кr, которые сходны с соответствующими элементами второго периода.

Порядок заполнения 5s-, 4d- и 5р-подоболочек такой же, как и для 4s, 3d и 4р. Далее, после заполнения 6s-орбитали, начинают заполняться 4f-орбитали. Элементы с незаполненной 4f-подоболочкой называются редкоземельными. Они обладают сходными химическими свойствами. Как и переходные металлы, редкоземельные элементы имеют почти вырожденные (близкие по энергии) орбитали. В конфигурациях, соответствующих основному состоянию, они имеют один 5d-электрон вслед за незаполненной 4f-подоболочкой; первый 5d-электрон появляется в La и затем больше не добавляются электроны в эту 5d-подоболочку вплоть до Hf. Наконец, после заполнения 5d-орбиталей (второй ряд переходных металлов) и далее 6р- и 7s-орбиталей начинают заполняться 5f-орбитали, что приводит к образованию актиноидов. Элементы, расположенные за ураном (92-й элемент периодической системы), образуются только при бомбардировке нейтронами тяжелых элементов и, как правило, имеют малое время жизни ^*).

^*) (Сведения, относящиеся к истории развития периодической классификации элементов, можно получить в следующих статьях: "Journal of Chemical Education", 11, 27, 217, 288 (1934); 16, 394 (1939); 25, 658, 662 (1948); 33, 69 (1956); 34, 30 (1957).)

Химия элементов делится на две главные области: химия переходных элементов и химия элементов основных групп. Элементы этих двух классов имеют мало общего, хотя в более высоковалентных состояниях и существуют некоторые общие черты. Хроматы и сульфаты, например, часто изоморфны, хотя химия хрома существенно отличается от химии серы. Химия переходных металлов первого ряда изучает главным образом их октаэдрические комплексы, которые будут рассмотрены в гл. 13. Переходные элементы второго и третьего рядов имеют много общего; например, Zr и Hf обладают почти одинаковыми химическими свойствами. Эта общность свойств вызвана "лантаноидным сжатием" - уменьшением радиуса одинаково заряженных ионов элементов от La до Lu, у которых происходит заполнение f-орбиталей. Сжатие приводит к тому, что радиус иона Hf⁴⁺ почти равен радиусу иона Zr⁴⁺, а не больше его.

Элементы основных групп с незаполненными s- и р-подоболочками делятся на два типа. Элементы, расположенные в таблице слева, например Li, Cs, Sn, легко отдают электроны, образуя катионы. Элементы же, расположенные справа, например О, F, I, легко присоединяют электроны и обычно встречаются в виде анионов.

Элементы подгрупп 2а и 3b имеют незаполненные низшие р-орбитали, которые обычно заполняются неподеленными парами электронов в соединениях элементов подгрупп 5b и 6b. Элементы этих подгрупп образуют множество комплексов.

Почти все элементы образуют соединения с водородом. Диапазон их широк: от солеподобных "ионных" гидридов, таких, как NaH, до гидридов переходных металлов, таких, как НСо(СО)₄. Особый интерес представляют гидриды бора, которые относятся к соединениям с электронным дефицитом, так как они образуют больше связей, чем позволяет электронная структура. Эти соединения обсуждаются в гл. 14.

Соединения ксенона с фтором и кислородом в настоящее время хорошо известны, но, за исключением возможно аналогичных им соединений криптона и радона, инертные газы химически неактивны.