Глава 5. Основные принципы теории валентности

Приемлемая теория валентности должна удовлетворять следующим требованиям:

1. Объяснить, почему вообще одни атомы вступают в соединения, а другие- нет (например, возможна реакция 2Н → Н₂, но невозможна реакция 2Не → Не₂), и вычислить энергии связи.

2. Объяснить, почему атомы соединяются в определенных отношениях (например, СН₄ - стабильная молекула, а СН₂, СН₅ и т. д. - нестабильные).

3. Нужно, чтобы теория валентности объяснила и, если возможно, предсказала длины связей и углы между ними.

В настоящей главе проводится предварительное обсуждение этих критериев.

Атомы объединяются в молекулы потому, что в таком процессе их полная энергия понижается, причем геометрия молекулы определяется расположением атомов, которое соответствует минимальной энергии системы. Если построить график зависимости суммы электронной энергии и энергии отталкивания ядер (Е) стабильной двухатомной молекулы от межъядерного расстояния r, то получим кривую, изображенную на рис. 5.1. Это кривая потенциальной энергии, определяющая колебания молекулы, которые обсуждаются более подробно в гл. 7. При малых расстояниях r между ядрами энергия в основном определяется энергией отталкивания ядер, которая стремится к бесконечности как 1/r. Величина r₀ есть равновесная длина связи, но нельзя утверждать, что ядра фиксированы в этом положении, поскольку такое утверждение противоречит принципу неопределенности. Даже в состоянии с минимальной энергией атомы колеблются, и r₀ обозначает среднее расстояние между ядрами в этом состоянии. D_e - электронная энергия диссоциации; однако измеряемая на опыте энергия диссоциации меньше ее на величину энергии нулевых колебаний, т. е. равна D_e - D₀.

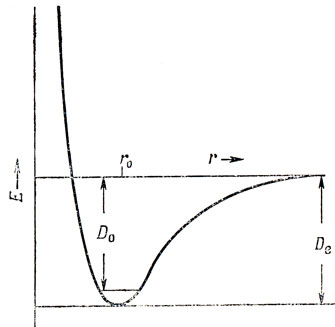
Рис. 5.1. Кривая потенциальной энергии двухатомной молекулы

Из экспериментальных данных следует, что существуют два основных типа химической связи - ионная и ковалентная. Молекулы, обладающие ионными связями, диссоциируют на ионы в полярных растворах; молекулы же с ковалентными связями такой диссоциации не обнаруживают. Согласно теории валентности Льюиса, атомы в случае ионной связи удерживаются кулоновскими силами, в случае же ковалентной связи - общей парой электронов, так что приходится вводить в рассмотрение какие-то новые силы (это определение включает и так называемую координационную связь). Как будет видно в дальнейшем, происхождение этих сил можно объяснить квантовомеханически, а понятия ионной и ковалентной связей относятся лишь к предельным случаям; реальные же связи носят промежуточный характер.

Рассмотрим сначала классическую электростатическую энергию взаимодействия двух атомов. Сила взаимодействия между двумя нейтральными атомами, расположенными на таком расстоянии, что их электронные облака практически не перекрываются, равна нулю (так как потенциал вне равномерно заряженной по объему сферы такой же, как если бы весь заряд был сосредоточен в центре). Когда электронные облака слегка перекрываются, появляется слабое притяжение, но когда электронное облако одного атома велико в области ядра другого, то возникают силы отталкивания, которые быстро растут при сближении ядер (все эти выводы следуют из классической электростатики). Энергию связи можно вычислить, рассматривая лишь электростатическое взаимодействие, но она оказывается чрезвычайно малой; например, для молекулы Н₂ она составляет всего лишь около 5% полной энергии связи.

Силы притяжения между положительными и отрицательными ионами возникают уже при таких расстояниях, когда электронные облака еще не перекрываются и, следовательно, энергия связи в этом случае велика; энергия получается интегрированием силы от бесконечности до некоторого r:

Однако энергия разрыва ионной связи определяется не только энергией притяжения ионов, так как не существует молекул (в газовой фазе), для которых продуктами диссоциации основного состояния являлись бы ионы. Наименьший потенциал ионизации имеет атом Cs (I = 3,86 эв), а наибольшим сродством к электрону обладает Сl (А = 3,83 эв), так что даже для CsCl энергетически выгоднее диссоциация на атомы, а не на ионы ^*). На рис. 5.2 показаны кривые потенциальной энергии NaCl, полученные на основе классической электростатической модели. Ионная связь имеет место только в том случае, если энергия кулоновского притяжения ионов превышает энергию I - А, необходимую для образования изолированных ионов.

^*) (Потенциал ионизации - это энергия, необходимая для удаления электрона из атома. Сродство к электрону - энергия, выделяющаяся в результате присоединения электрона. Сродство к электрону есть потенциал ионизации отрицательного иона.)

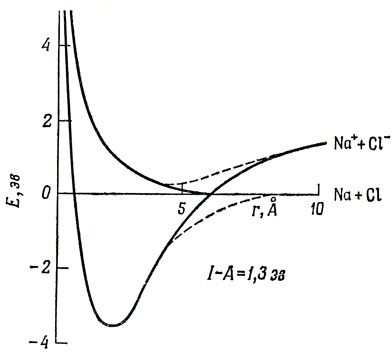
Рис. 5.2. Кривые потенциальной энергии молекулы NaCl

NaCl диссоциирует в полярных растворах на ионы потому, что ионы имеют значительно большую энергию связи с растворителем (энергия сольватации), чем недиссоциированная молекула. Этой энергии достаточно, чтобы скомпенсировать равную 5 эв энергию диссоциации на ионы в газовой фазе. Энергия сольватации имеет преимущественно электростатическое происхождение.

Как видно из рис. 5.2, кривые потенциальной энергии для ионов и нейтральных атомов пересекаются (в точке, где I - А = е²/r). Как будет видно из последующих глав, в действительности состояние молекулы нельзя рассматривать как чисто ионное или вовсе не имеющее ионного характера: всегда встречается промежуточный случай. Правильнее сказать, что связь содержит некоторый процент ионности. Одним из следствий этого смешивания ионной и ковалентной связи является то, что, если кривые потенциальной энергии для состояний, диссоциирующих на Na⁺ + Cl^- и Na + Cl, рассчитаны точно, они не пересекаются, что видно из рис. 5.2, где эти кривые обозначены пунктирными линиями. Это важный общий результат квантовомеханического рассмотрения, известный, как правило непересечения термов, доказательство которого приводится в гл. 10. Оно означает, что, хотя в основном состоянии молекула NaCl является преимущественно ионной, тем не менее продуктами диссоциации этого состояния в газовой фазе будут нейтральные атомы.

Если потенциал ионизации атома велик, то тенденция отдавать электроны другим атомам у него выражена слабо; если же велико сродство к электрону, то атом стремится присоединить электроны. Общее стремление атома к увеличению заряда определяется суммой этих двух величин. Малликен предположил, что величина

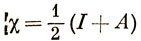
наилучшим образом может служить основой для построения шкалы электроотрицательностей элементов. Ионный характер связи АВ определяется тогда величиной |χ_А - χ_В|. В табл. 5.1 приведена часть шкалы электроотрицательностей по Малликену. Заметим, что электроотрицательность, как правило, возрастает в ряду элементов слева направо и уменьшается в группе сверху вниз. Наибольшей электроотрицательностью обладает атом F, хотя сродство к электрону больше для атома Сl. Шкала электроотрицательностей, предложенная Полингом, будет обсуждаться в гл. 11.

Таблица 5.1. Шкала электроотрицательностей по Малликену [70]

Хотя шкалы электроотрицательности оказались качественно очень полезными Для химиков при обсуждении ионного характера связи, в количественном отношении эти величины не очень надежны. Например, дипольные моменты галоидоводородов хорошо коррелируют с величинами электроотрицательностей галогенов, однако такая корреляция не имеет места для других молекул. Ясно также, что электроотрицательность атома зависит от типа связи, которую он образует. Например, кислотность ацетилена значительно выше, чем кислотность метана, поэтому приходится заключить, что атом углерода в ацетилене более электроотрицателен, чем в метане.

Обратимся теперь к ковалентной связи. Существуют два теоретических подхода, используемых для ее объяснения: метод молекулярных орбиталей (МО) и метод валентных связей (ВС). Оба эти метода позволяют объяснить, почему льюисовская схема электронного спаривания приводит к устойчивой связи, но, на первый взгляд, оба подхода совершенно различны. В следующих главах, где подробно обсуждаются оба метода, будет показано, что в своей простейшей форме они носят очень приближенный характер и описывают лишь предельные случаи ковалентной связи. Более точное описание ковалентной связи лежит где-то между ними.

Метод МО является естественным распространением теории атомных электронов на случай электронов в молекуле. Если существуют атомные орбитали, то почему бы не предположить существование молекулярных орбиталей? Поскольку электронные функции в атомах простираются вплоть до бесконечности, мы полагаем, что молекулярные орбитали распространяются по крайней мере на всю область, занимаемую молекулой. Электроны могут занимать эти "делокализованные" орбитали с тем же ограничением, что и в случае атомов - каждая орбита ль может быть занята не более, чем двумя электронами.

Чтобы объяснить, почему энергия молекулы Н₂ меньше, чем сумма энергий двух водородных атомов, достаточно понять, почему МО молекулы Н₂, имеющая наиболее низкую энергию, энергетически выгоднее, чем 1s-орбиталь атома Н. Объяснение этого факта заключается в следующем: электроны, расположенные на МО молекулы Н₂, находятся в поле двух протонов, а не одного, как в атоме. Для сравнения заметим, что полная электронная энергия атома Не равна 74 эв, а двух атомов водорода составляет 27 эв. Энергия отталкивания ядер в Н₂ (20 эв) недостаточна, чтобы скомпенсировать это понижение потенциальной энергии электронов.

Однако изменение энергии двух атомов водорода при образовании ими связи составляет только 18% от их полной энергии, поэтому справедливо предположение, что орбитали Н₂ довольно близки к АО водородных атомов. Действительно, в области, близкой к одному из ядер, электрон будет находиться в основном под действием потенциального поля этого ядра, так что в этой области МО должна быть близка к соответствующей АО. Именно это обстоятельство лежит в основе приближения линейных комбинаций атомных орбиталей (ЛКАО) при построении МО, которое будет детально рассмотрено в гл. 10. Наглядно можно представить себе образование низшей МО молекулы Н₂ из двух водородных 1s-орбиталей, как это показано на рис. 5.3. Если бы два ядра слились, получилась бы 1s-орбиталь атома Не.

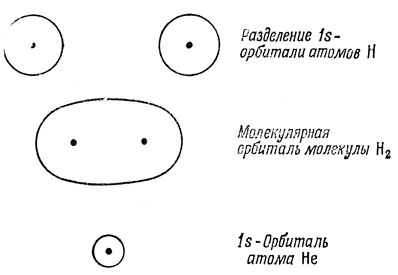
Рис. 5.3. Корреляция между 1s-орбиталями атомов Н и Не и молекулярной орбиталью молекулы Н₂

Метод ВС есть, по существу, перевод теории Льюиса на язык квантовой механики. Предполагают, что электроны в молекуле находятся скорее на атомных орбиталях, чем на молекулярных, но допускают, что если две АО перекрываются друг с другом, то нельзя с уверенностью сказать, на какой именно АО находится электрон, поскольку электроны не различимы. Следует написать для молекулы такую волновую функцию, которая допускала бы возможность обнаружения электрона на любой из двух АО. Другими словами, волновая функция, описывающая электронную пару, должна отражать возможность делокализации электрона, что, как видно из метода МО, и создает эффект стабилизации.

И в методе молекулярных орбиталей, и в методе валентных связей сильное перекрывание АО приводит к делокализации электрона и возникновению сильной связи. Поэтому перекрывание АО играет основную роль в обоих методах теоретического изучения ковалентной связи. Количественно степень перекрывания определяется величиной интеграла перекрывания, который для двух АО φ_а и φ_b есть, по определению,

где интегрирование проводится по всему пространству.

На рис. 5.4, а показаны некоторые случаи взаимной ориентации АО, приводящие к значительному перекрыванию, и, следовательно, сильным связям. Следует отметить, что при вычислении S_аb существенно лишь соотношение знаков волновых функций, а не знак каждой из них в отдельности. Позже, при более подробном обсуждении метода МО, будет показано, что если S_ab отрицательно, как, например, на рис. 5.4, б, то это приводит к увеличению энергии системы (случай разрыхления) ^*). В некоторых случаях, хотя две орбитали и перекрываются, интеграл перекрывания равен нулю, вследствие того, что вклады областей положительного и отрицательного перекрывания взаимно компенсируются. Это показано на рис. 5.4, в. Если S_ab = 0, то имеет место случай несвязывающего состояния.

^*) (Знак интеграла перекрывания функций не имеет физического значения, так как любая из функций φ_а и φ_b определяется с точностью до постоянного фазового множителя е^iα, где α - любое вещественное число, и, в частности, любую функцию можно взять с обратным знаком. - Прим. ред.)

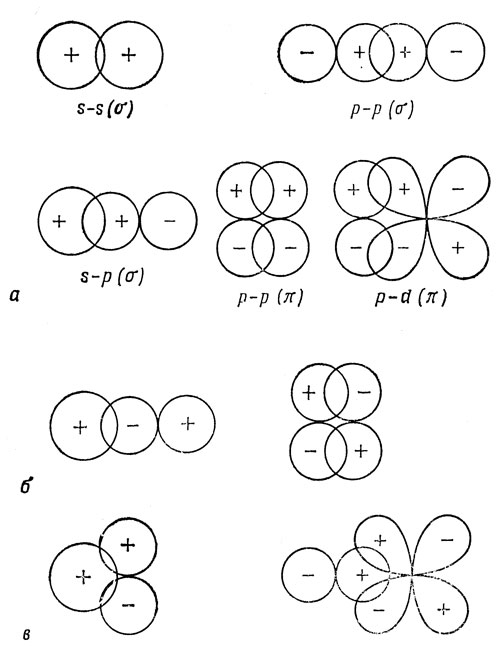
Рис. 5.4. Перекрывание атомных орбиталей, приводящее к положительному (а), отрицательному (б) и нулевому (в) значениям интеграла перекрывания (S)

Спин электрона играет важную роль в теории ковалентной связи. При описании молекулы Н₂ по методу МО принимают, что наиболее низкая МО занята двумя электронами, которые должны иметь противоположные спины. Если же сближаются два атома водорода, электроны которых имеют одинаковые спины, то только один из электронов может попасть на самую низкую МО, другой же должен занять МО с более высокой энергией. Эта орбиталь является сильно разрыхляющей, и энергия состояния в целом соответствует отталкиванию. То же самое имеет место и в методе ВС. Таким образом, если электроны, находящиеся на перекрывающихся АО, имеют одинаковые спины, то это приводит к отталкиванию. Этот вывод согласуется с принципом Паули, по которому никакие два электрона не могут иметь одинаковые пространственные функции, если одинаковы их спины. Для лучшего перекрывания двух АО желательно, чтобы оба электрона описывались одинаковыми пространственными функциями, а это возможно только в том случае, если у них противоположны спины. Теперь можно легко понять, почему инертные газы образуют очень мало химических соединений. Их АО или заполнены полностью или вовсе не заполнены, и перекрыванию заполненных АО с какой-либо АО, содержащей электрон, будет противодействовать принцип Паули. По той же причине, если молекула находится в состоянии, в котором спины всех ее электронов, расположенных на самых низких по энергии орбиталях, спарены, присоединение других атомов будет затруднено.

Элементы основных групп, имеющие незаполненные s- и р-оболочки, стремятся к соединению с другими атомами, пока спины всех электронов не будут спарены. Переходные и редкоземельные элементы, с другой стороны, образуют стабильные молекулы, в которых есть неспаренные электроны. Это имеет место потому, что d- и f-орбитали в основном расположены в области, где сосредоточена электронная плотность внутренних заполненных оболочек (например, 3d-орбиталь проникает в область заполненных 3s- и 3р-оболочек, как это видно из рис. 5.5). Отталкивание, действующее со стороны электронов этих заполненных оболочек, не позволяет получить большое перекрывание между d- или f-орбиталями и орбиталями присоединяемых атомов. В гл. 13 химические свойства переходных элементов рассматриваются на основе теории, согласно которой d-орбитали очень слабо участвуют в образовании ковалентной связи.

Рис. 5.5. Радиальные волновые функции иона V²⁺ [86]

Элементы 2-й группы подобны инертным газам в том отношении, что имеют только спаренные электроны. Однако энергия, необходимая для нарушения этого спаривания, довольно мала (для атома Be достаточно около 4 эв для возбуждения электрона с 2s-орбитали на 2p-орбиталь, и, таким образом, оба электрона после возбуждения могут участвовать в образовании связи). Выигрыш в энергии, получаемый при образовании связей, более чем достаточен, чтобы компенсировать энергию первоначального возбуждения. Это иллюстрируется кривой потенциальной энергии молекулы ВеН, представленной на рис. 5.6. Здесь, так же, как на рис. 5.2, учтено правило непересечения. Среди двухатомных гидридов, образованных атомами второго периода (от LiH до HF), ВеН имеет самую низкую энергию диссоциации, так как только для Be требуется возбудить атом, прежде чем электроны станут способными к образованию связи.

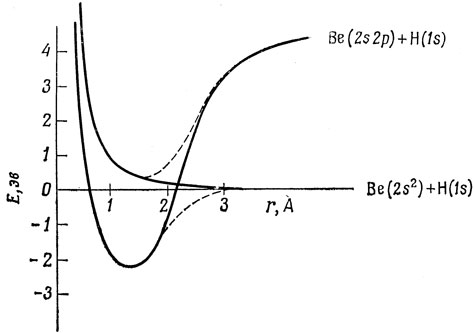
Рис. 5.6. Кривые потенциальной энергии молекулы ВеН

Приводимое объяснение образования ковалентных связей бериллием поставило нас в довольно трудное положение; на первый взгляд кажется, что после возбуждения электроны могут образовывать связи различного вида. Один электрон находится на 2р-орбитали, и это может привести к образованию связи, если соответствующим образом ориентированная орбиталь приближается к любому из двух "лепестков". С другой стороны, электрон, расположенный на s-орбитали, может образовывать связь независимо от того, в каком направлении происходит перекрывание с другой орбиталью. Эти идеи несовместимы со свойствами молекулы типа ВеН₂, которая, если бы она существовала, должна была бы быть линейной, с двумя одинаковыми связями ВеН ^*).

^*) (ВеН₂ известна только в форме полимера. Наиболее подходящий пример молекулы, имеющей предполагаемую структуру ВеН₂, - молекула Hg(CH₃)₂, в которой связи Hg - С расположены на одной прямой.)

Очевидно, что если нужно использовать представление об электронных парах, образующих связь, то две орбитали, участвующие в образовании связи, должны быть эквивалентны, а ориентация их должна быть такой, чтобы их "лепестки" были направлены вдоль одной прямой в противоположные стороны. Можно построить так называемые гибридные орбитали, обладающие этим свойством и определенные следующим образом:

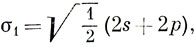
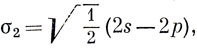
где √1/2 - нормировочная постоянная. На рис. 5.7 показана приближенная форма этих гибридных орбиталей, которые называются sp-гибридами. Следует отметить, что они имеют еще более ярко выраженное свойство направленности, чем р-орбитали, так как они образуют достаточно сильную связь только в том случае, если атом водорода приближается со стороны положительного "лепестка" (см. рис. 5.8).

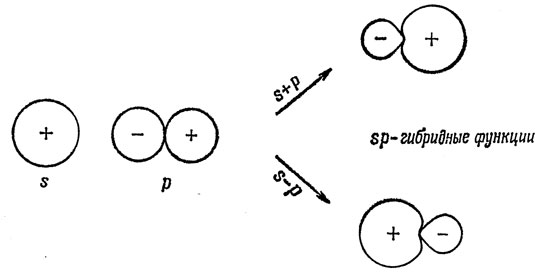
Рис. 5.7. Формирование sp-гибридных функций

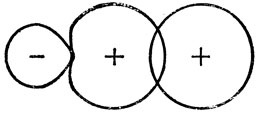
Рис. 5.8. Связь посредством перекрывания sp-гибридной орбитали s-орбиталью

Гибридизация играет важную роль в описании связей, образуемых всеми элементами, кроме водорода, но, пожалуй, она наиболее важна при описании углеродных связей. В основном состоянии атома углерода 1s- и 2s-орбитали заполнены, и два электрона находятся на 2p-орбиталях [принято говорить, что он имеет электронную конфигурацию (1s)² (2s)² (2p)²]. При этом следовало бы ожидать, что атом будет двухвалентным и 2р-электроны будут образовывать связи под углом 90° друг к другу. Однако почти во всех своих соединениях углерод четырехвалентен. Чтобы объяснить этот факт, мы вынуждены предположить, что состояние образующего связи углерода соответствует электронной конфигурации (1s)² (2s) (2р)³, и тогда 2s-электрон и три 2р-электрона могут участвовать в образовании связей.

Метан содержит четыре эквивалентные связи СН, направленные к вершинам тетраэдра. Чтобы сопоставить этим связям четыре эквивалентные электронные пары, необходимо построить четыре эквивалентные тетраэдрически ориентированные гибридные орбитали из одной 2s- и трех 2р-орбиталей атома углерода. Поскольку каждая гибридная орбиталь должна содержать одну и ту же долю s-функций и р-функций, сразу получаем, что для каждой из них s-характер равен 1/4, а р-характер составляет 3/4 ^*). Таким образом, плотность вероятности Ψ₂² для каждой гибридной орбитали должна содержать 1/4 ψ_s² и 3/4 ψ_р². Чтобы получить более детальный явный вид гибридных орбиталей, выберем определенную ориентацию тетраэдра по отношению к осям декартовой системы координат. Наиболее удобно, по-видимому, вписать тетраэдр в куб, грани которого параллельны декартовым осям, как это показано на рис. 5.9.

^*) (s-Характером называют квадрат модуля коэффициента при s-функции, входящей в нормированную на единицу гибридную орбиталь. - Прим. перев.)

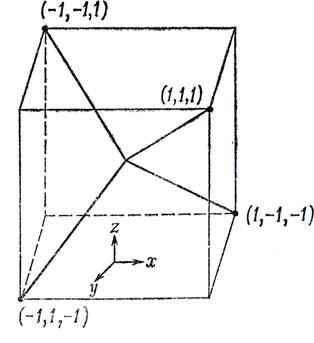
Рис. 5.9. Тетраэдрические связи, направленные к вершинам куба. Начало координат помещено в центре куба

На рисунке вершины тетраэдра обозначены тройками чисел, являющихся их декартовыми координатами. Из соображений симметрии ясно, что гибридная орбиталь, направленная к вершине [1, 1, 1], должна содержать равные доли p_x-, p_y- и p_z-функций. Учитывая сказанное выше, сразу получаем, что эта гибридная орбиталь должна иметь вид

Относительный вклад каждой из четырех орбиталей, содержащихся в этом гибриде, определяется квадратом соответствующего коэффициента. Аналогичным образом можно построить

В задаче 3.3 предлагалось показать, что две атомные орбитали одного и того же атома ортогональны, т. е.

Легко показать, что построенные нами четыре гибридные орбитали также ортогональны. Например,

Эти условия ортогональности выражают независимость четырех гибридных функций (роль ортогональности подробно обсуждается в гл. 6).

Четыре гибридные орбитали, использованные нами для построения связей, направленных к вершинам тетраэдра, называются sр³-гибридными орбиталями. Они похожи по форме на sp-гибридные орбитали и подобно последним обладают сильно выраженной направленностью. Контурная диаграмма sр³-гибридной функции приведена на рис. 5.10.

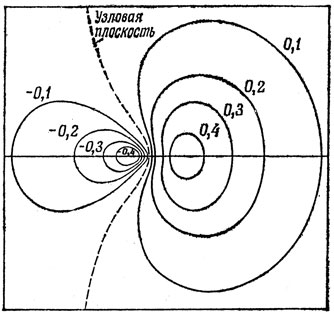
Рис. 5.10. Контуры для sp³-гибридной орбитали

В олефинах и ароматических углеводородах атом углерода соединяется с тремя другими атомами, лежащими в одной плоскости, образуя связи, расположенные под углом 120° друг к другу. Пусть атомы лежат в плоскости yz; тогда, очевидно, углеродная р_х-орбиталь не дает вклада в гибридные орбитали, направленные вдоль этих трех связей. Поэтому необходимые в этом случае три гибридные орбитали можно построить из s-, p_y- и p_z-AO, и они называются sp²-гибридными орбиталями. Если все три гибридные функции эквивалентны, то в каждой из них s-характер равен 1/3, а p-характер составляет 2/3.

Если оси координат выбрать так, как это показано на рис. 5.11, то гибридная орбиталь, направленная к атому А, не может содержать функцию p_y, потому что эта функция имеет узловую плоскость, проходящую через атом А. Отсюда следует, что

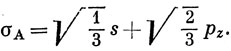
Чтобы получить вид других гибридных орбиталей, посмотрим, что произойдет, если изменить ориентацию каждой из функций, входящих в выражение (5.8), на угол 2π/3: σ_А → σ_В, s → s и р_z → р_z cos 2π/3 + p_y sin 2π/3. Подстановка этих новых функций в уравнение (5.8) дает

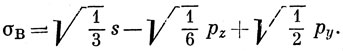
Аналогично, рассматривая вращение на угол -2π/3, получим

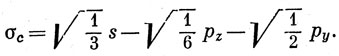
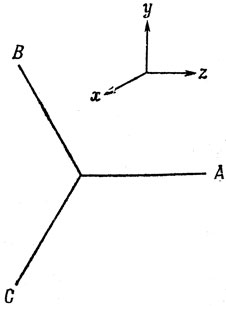
Рис. 5.11. Расположение связей в случае sp²-гибридизации

Гибридные орбитали, построенные таким образом, фактически полностью определяются симметрией задачи. Можно показать также, что они удовлетворяют требованию максимальности перекрывания орбиталей, включаемых в связи. Если перекрывание максимально, то, грубо говоря, и сила связи наибольшая; поэтому максимальность перекрывания можно использовать как общий критерий ля построения наилучших гибридных орбиталей. В случае метана, например, можно построить четыре гибридные орбитали, для которых максимальна сумма интегралов их перекрывания с четырьмя спаренными с ними водородными 1s-орбиталями. Это приведет к тому же набору орбиталей, который был получен на основе рассмотрения симметрии. Существует общий метод построения оптимальных орбиталей, соответствующих максимуму перекрывания в случае, когда нет никакой симметрии ^*).

^*) (См. работу [71] и приведенные в ней ссылки.)

По углам между связями в молекуле можно судить о виде гибридизации орбиталей, участвующих в образовании связей. Ограничиваясь s- и р-орбиталями, можно записать следующее:

Связи, углы между которыми заключены между 90 и 180°, соответствуют промежуточной гибридизации. Из s- и р-орбиталей невозможно построить ортогональные гибридные орбитали, углы между которыми были бы меньше 90°. Поэтому молекулам типа циклопропана приписывают существование изогнутых связей (рис. 5.12). Это описание согласуется с тем фактом, что такие связи значительно слабее обычной связи С - С.

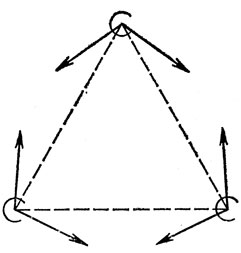
Рис. 5.12. Изогнутые связи в циклопропане. Стрелки указывают направления оптимально гибридизованных орбиталей

Если d-орбитали участвуют в гибридизации, то можно построить гибридные функции, соответствующие другим расположениям связей; например,

Другие примеры будут обсуждаться в этой главе позже.

Проведенное обсуждение гибридизации носило апостериорно-дедуктивный характер. Можно сказать, что гибридизация очень полезна при описании волновых функций электронов в связях и, как будет видно дальше, на особенно существенна в методе ВС, однако не позволяет, вообще говоря, объяснить форму молекул. Строго говоря, гибридизация представляет собой просто математический прием, используемый в теоретической химии, но оказывающийся весьма полезным при качественном описании химической связи, как будет показано на многочисленных примерах, рассмотренных в этой книге.

Форма молекулы определяется в основном вкладами в энергию двух величин: энергий связи, которые зависят от перекрывания, и энергии электростатического отталкивания между электронами различных пар. Эта последняя часто преобладает. Например, в молекуле Hg(CH₃)₂ электростатическое отталкивание между электронами связей Hg - С минимально, если молекула линейна. В молекуле BF₃ отталкивание трех электронных пар наименьшее, если атомы расположены в одной плоскости, а углы между связями равны 120°. В молекуле СН₄ отталкивание четырех электронных пар, образующих связи, минимально при тетраэдрическом расположении атомов.

Теперь приведем несколько примеров, которые иллюстрируют основные свойства ковалентной связи, обсуждавшиеся в настоящей главе.

1. Этан, этилен и ацетилен

Принято называть связь между атомами углерода в этане, этилене и ацетилене простой, двойной и тройной соответственно, так что во всех этих соединениях углерод четырехвалентен. Что это означает на языке квантовой механики? На рис. 5.13 показаны конфигурации этих трех молекул. Ацетилен - линейная молекула, этилен - плоская, а в этане две группы СН₃ обладают почти полной свободой вращения друг относительно друга вокруг связи С - С. Рассматривая углы между связями, можно сделать вывод, что в этане углерод находится в состоянии sp³-гибридизации, в этилене - sp², а в ацетилене - sp-гибридизации.

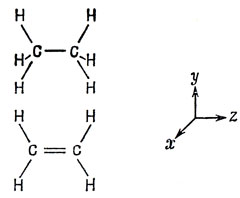
Рис. 5.13. Схемы связей в некоторых углеродных соединениях

В этане три sр³-гибридные орбитали каждого атома углерода участвуют в образовании связей с атомами водорода, а четвертая - в образовании связи С - С, которая аксиально симметрична и называется σ-связью. Схематически это показано на рис. 5.14.

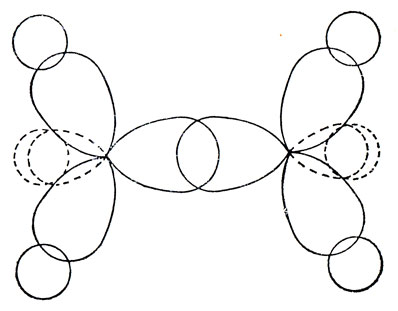
Рис. 5.14. Связь посредством sр³-гибридных орбиталей в этане

В этилене две sр²-гибридные орбитали каждого атома углерода участвуют в образовании связей С - Н, а третья - в образовании σ-связи между атомами углерода. Одна из 2р-АО углерода не используется при построении sр²-гибридных функций, а именно р_х-АО, для которой плоскость молекулы является узловой плоскостью. Две углеродные р_х-орбитали могут образовать двухэлектронную связь между атомами углерода. Электронная плотность этих двух электронов равна нулю в плоскости молекулы, и связь такого типа называют π-связью. σ- и π-Связи в этилене показаны на рис. 5.15.

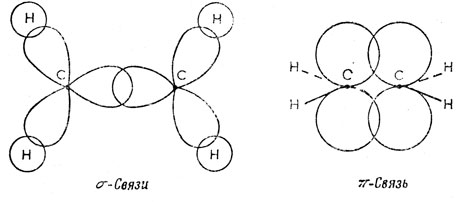
Рис. 5.15. σ- и π-Связи в этилене

В ацетилене углеродные sp-гибридные орбитали образуют связи С - Н и σ-связь между атомами углерода. Для каждого из атомов углерода существуют две р-орбитали, не участвующие в образовании σ-связей, так что они могут быть использованы при построении π-связей. Если оси координат выбраны так, как это показано на рис. 5.13, то можно сказать, что существуют р_х - р_х π-связь и p_y - p_yπ-связь. Но единственной величиной, которую можно измерить, является полная электронная плотность этих π-связей, осесимметричная относительно линии связи С - С и равная нулю на этой линии связи ^*). В гл. 10 более подробно анализируется смысл символов σ и π, использованных здесь.

^*) (Плотность р_x² + р_y² обладает аксиальной симметрией по отношению к линии связи С - С.)

Следует ожидать, что π-связь слабее σ-связи, потому что интеграл перекрывания между двумя рπ-АО значительно меньше, чем между двумя σ-гибридными АО. Появление π-связей уменьшает расстояние между атомами углерода с 1,54 А в этане до 1,35 А в этилене, а наличие еще одной π-связи в ацетилене приводит к дальнейшему уменьшению межатомного расстояния до 1,21 А. На основе анализа термохимических данных было обнаружено, что каждому из трех рассмотренных типов связи между атомами углерода можно приписать значение энергии связи, которое приблизительно постоянно во всех молекулах. Полинг [66] приводит для этих энергий следующие значения:

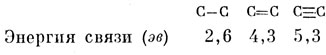
2. Бензол

Для бензола можно изобразить две классические валентные схемы, которые принято называть структурами Кекуле:

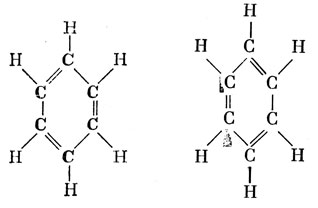
Углы между связями в бензоле равны 120°, поэтому естественно для описания связей в этой молекуле использовать sр²-гибридные функции, как и в случае этилена.

Из них можно построить систему простых связей С - Н и С - С, которая называется системой σ-связей. У каждого атома углерода остается одна р-орбиталь, пригодная для образования π-связи, как показано на рис. 5.16.

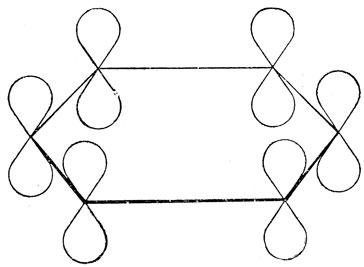
Рис. 5.16. π-Связывающие орбитали бензола

Существует много химических и физических данных, из которых следует, что молекула бензола имеет структуру правильного шестиугольника, а не является системой альтернирующих длинных и коротких связей, быстро меняющихся местами согласно следующей схеме:

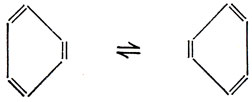
Однако, исходя из рπ-АО, невозможно построить двухэлектронные связи, образующие правильный шестиугольник. Каждая из орбиталей перекрывается в одинаковой степени как с орбиталью, расположенной слева от нее, так и с орбиталью справа. Приближенно можно изобразить распределение плотности π-электронов в виде двух колец, одно из которых расположено над плоскостью молекулы, а другое - под ней (см. рис. 5.17), и рассматривать, таким образом, π-связи как делокализованные связи, простирающиеся по всему кольцу. Длина связи С - С равна 1,40 А, т. е. имеет значение, промежуточное между длинами связей С - С в этане и этилене. Можно сказать, что на каждую связь между атомами углерода приходится половина π-связи.

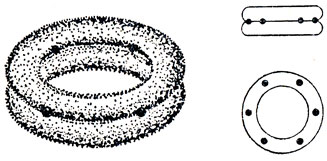
Рис. 5.17. Делокализованные π-связи в бензоле

Именно благодаря делокализации π-электронов молекула бензола чрезвычайно стабильна. Для бензола более характерны химические реакции замещения, а не реакции присоединения, идущие легко для олефинов. Подробное рассмотрение π-связи в бензоле и родственных ему соединениях проводится в гл. 15. Здесь же только отметим, что системы с делокализованными π-электронами имеют важное значение в химии. Такие системы присутствуют не только в соединениях бензола, но и во всех соединениях, которые содержат сопряженные ненасыщенные связи, как, например,

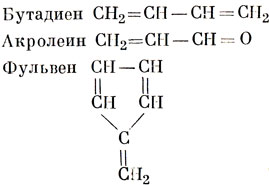
Эти молекулы содержат делокализованные π-электроны, хотя их можно представить только одной классической валентной схемой.

3. Аммиак и вода

Можно было бы ожидать, что такие простые молекулы, как молекулы аммиака и воды, не должны представлять большой трудности в теории валентности. К сожалению, это не так.

Атом азота в основном состоянии имеет электронную конфигурацию (1s)² (2s)² (2р)³. Все три р-электрона могут участвовать в образовании связей, и следует ожидать, что в молекуле NH₃ все три связи N - Н образуют между собой углы 90°. Кислород имеет в основном состоянии конфигурацию (1s)² (2s)² (2p)⁴; два р-электрона могут участвовать в образовании связей, так что угол между ними должен быть равен 90°. На самом же деле угол между связями в молекуле аммиака равен 107°, а в молекуле воды составляет 104°. Эти углы довольно близки к тетраэдрическому углу 109°; появляется соблазн утверждать, что структура этих молекул обусловлена в большей степени отталкиванием электронов различных пар, чем характером орбиталей,на которых находятся неспаренные электроны в основном состоянии атома.

В обеих молекулах имеется по четыре электронных пары (не считая 1s-электронов кислорода или азота). Электронное отталкивание стремится ориентировать связи так, чтобы они были направлены к вершинам тетраэдра, так что необходимо использовать sp³-гибридизацию для описания связей. Однако для возникновения такой гибридизации нужна дополнительная энергия (11 эв для атома азота), чтобы перевести (промотировать) 2s-электрон в 2p-оболочку, и это обстоятельство препятствует правильному тетраэдрическому расположению. Значительно большая энергия нужна для гибридизации в углероде, и, во всяком случае, она компенсируется образованием двух дополнительных связей. Для атомов же азота и кислорода промотирование не приводит к увеличению валентности, так что единственная возможность для компенсации энергии промотирования - это увеличение прочности связи.

Хотя рассмотрение углов между связями в молекулах NH₃ и Н₂O показывает, что электронное отталкивание является чрезвычайно существенным фактором в образовании структуры молекулы, для гидридов элементов следующих периодов углы между связями близки к 90° (94° в РН₃, 93° в H₂S). Если электронное отталкивание столь важно при рассмотрении элементов второго периода, то почему же это не так для элементов следующих периодов?

Для объяснения этого факта предложены два подхода. Полинг [66] принимает в исходном приближении угол 90° и то, что в молекуле Н₂O угол больше 90°, объясняет отталкиванием полярных связей О - Н (см. рис. 5.18). При другом подходе, предложенном Диккенсом и Линнетом [21], принимают в исходном приближении угол между связями равным 109°, как это следует из распределения электронов в конфигурации инертного газа (ионы О^2- и N^3- изоэлектронны неону). Искажение этого угла обусловлено тем, что протоны оттягивают связывающие пары электронов от центрального атома; происходит уменьшение энергии отталкивания этих пар по сравнению с парами, не участвующими в образовании связей, и, следовательно, уменьшение угла между связями. В обоих подходах различие между соединениями элементов второго и третьего периодов объясняется тем, что элементы третьего периода имеют меньшую электроотрицательность, так что их электроны более сильно притягиваются атомами водорода. Это приводит к уменьшению дипольного отталкивания в теории Полинга и отталкивания между электронными парами, рассматриваемого Диккенсом и Линнетом.

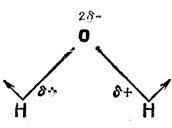
Рис. 5.18. Отталкивание полярных ОН-связей

Однако имеется другое и более существенное в обсуждаемых вопросах различие между элементами второго и третьего периодов. Для элементов второго периода интеграл перекрывания между 2s-орбиталью и водородной 1s-орбиталью (при равновесном расстоянии) значительно больше, чем интеграл перекрывания, содержащий 2р-орбиталь. Для элементов же третьего периода перекрывание больше для 3р-орбитали, чем для 3s-орбитали. Именно поэтому при включении в гибридную функцию s-орбиталей выигрыш в перекрывании для элементов второго периода значительнее, и в силу этого для них больше угол между связями (что обусловлено большей величиной s-характера). В табл. 5.2 приведены соответствующие численные данные.

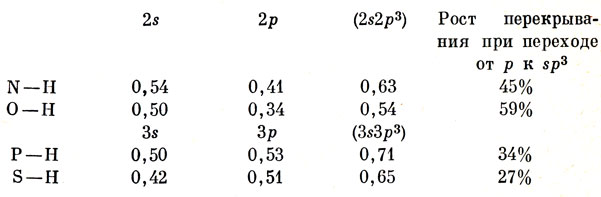
Таблица 5.2. Интегралы перекрывания между s-, s-, sр³-гибридами и водородными 1s-орбиталями (вычислены Маррелом и Рандичем при использовании самосогласованных орбиталей)

На первый взгляд может показаться, что серьезным недостатком квантовой механики является неспособность предложить одну ясную и последовательную теорию для объяснения величин углов между связями в молекулах, но на самом деле, как видно, эта задача является одной из наиболее сложных. Полная электронная энергия молекулы Н₂O примерно равна 2000 эв. Это значение энергии получается из решения уравнения Шредингера для основного состояния молекулы. Энергия диссоциации молекулы составляет 10 эв, а энергия, необходимая для изменения угла между связями от 104 до 90° - около 0,1 эв. Это означает, что если мы хотим путем расчета, исходя только из общих принципов квантовой механики, показать, что в молекуле Н₂O угол между связями равен 104°, а не 90°, то мы должны решить уравнение Шредингера для различных конфигураций ядер с точностью по крайней мере до 0,1 %. Наилучший расчет молекулы воды выполнен Бойсом и сотр. [5]. Их результаты приведены в табл. 5.3. Из этих данных ясно, что чрезвычайно трудно объяснить величину угла между связями в молекуле воды с помощью последовательного квантовомеханического расчета.

Таблица 5.3. Расчеты для молекулы воды

4. Высшие фториды фосфора, серы и хлора ^*)

^*) (Этот раздел можно при первом чтении опустить.)

Во втором периоде таблицы Менделеева элементы групп с 5-й по 7-ю имеют максимальные валентности - три, два и один соответственно, эти числа отвечают числу неспаренных электронов в L-оболочке. В третьем периоде, однако, элементы тех же групп могут иметь большую валентность. Чтобы обсудить этот факт, выберем в качестве примера молекулы PF₅ и ClF₃.

Фосфор имеет пять электронов на 3s- и 3р-орбиталях, а сера - шесть. Если бы все эти электроны были неспарены, они могли бы участвовать в образовании двухэлектронных связей и были бы возможны соединения типа PF₅ и SF₆. Почему же элементы третьего периода могут иметь столько неспаренных электронов, а элементы второго периода нет? Дело заключается в том, что элементы третьего периода имеют сравнительно глубоко лежащие вакантные орбитали такого же размера, как 3s- и 3р-орбитали, которые также необходимо учитывать: это 3d-орбитали. Следует подчеркнуть, что не сравнительно низкая энергия этих 3d-орбиталей (на самом деле, 4s- и 4р-орбитали дают более глубокие уровни энергии, чем 3d-орбитали) позволяет включать их при описании связи, а именно приблизительно такая же протяженность их, как 3s- и 3р-орбиталей. Это означает, что когда мы строим гибридную орбиталь с помощью 3s-, 3р- и 3d-орбиталей, то каждая из трех компонент вносит существенный вклад в перекрывание этой гибридной орбитали с орбиталями фтора. Если бы 3d-орбитали были более протяженными, чем 3s- или 3р-орбитали, то на расстоянии, при котором перекрывание велико для 3d-орбитали, оно было бы мало для 3s- и 3р-орбиталей, и наоборот, когда 3s- и 3р-орбитали имеют большое перекрывание с орбиталями фтора, 3d-орбиталь должна бы дать малое перекрывание. Энергия возбуждения 2р → 3d для кислорода ненамного больше, чем энергия возбуждения 3р → 3d для серы, но размеры 3d-орбитали значительно больше, чем размеры 2s- или 2р-орбиталей, так что любой 3d-характер в гибридной орбитали, содержащей также 2s- и 2р-функции, незначительно увеличивает ее способность к перекрыванию.

PF₅ имеет структуру тригональной бипирамиды, как показано на рис. 5.19. Такое расположение связей будет соответствовать наименьшей энергии отталкивания между пятью электронными парами.

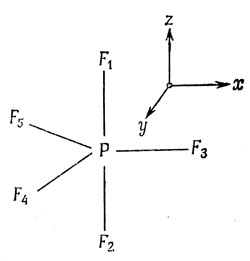
Рис. 5.19. Выбор координатных осей для PF₅

Рассмотрим более подробно вид гибридных функций для молекулы PF₅. Оси координат выберем так, как это показано на рис. 5.19, и атомы фтора пронумеруем в соответствии с этим рисунком. Пусть φ₁ ... φ₅ есть 2р-орбитали фтора, направленные к атому фосфора; эти орбитали наиболее важны для связи. Наилучшим способом получения гибридных орбиталей было бы построение их, основанное на условиях максимума интегралов перекрывания с орбиталями φ₁ ... φ₅. Чтобы сделать это, сначала нужно вычислить интегралы перекрывания между 3s-, 3р- и 3d-орбиталями фосфора и орбиталями фтора. Это не трудно, так как таблицы таких интегралов опубликованы, например, в работе [60]. Однако качественно форму гибридных орбиталей можно получить, просто считая, что эти интегралы перекрывания пропорциональны проекциям 3s-, 3р- и 3d-орбиталей на направления связей Р - F; такое приближение было впервые предложено Полингом [66]. Это допущение наряду с другими равносильно предположению, что радиальные части этих орбиталей одинаковы, по крайней мере в той области, которая вносит основной вклад в перекрывание. В таком приближении мы можем считать интегралы перекрывания просто пропорциональными значению соответствующей угловой функции на направлении связи (угловые функции приведены в табл. 3.1).

3s-Орбиталь перекрывается в одинаковой степени со всеми пятью орбиталями фтора, так что можно написать

где S - число, зависящее главным образом от радиальной части Зя-орбитали. Из соображений симметрии следует, что интегралы перекрывания 3р_z-орбитали с φ₁ и φ₂ одинаковы по величине и противоположны по знаку, но отличаются от соответствующих величин для орбиталей φ₃, φ₄ и φ₅, которые все лежат в узловой плоскости 3р_z-орбитали. Таким образом, учитывая вид функций, приведенных в табл. 3.1, получаем

Выпишем все эти интегралы перекрывания в виде таблицы; элемент таблицы, находящийся на пересечении строки, обозначенной d_z², и столбца, обозначенного φ₂, представляет собой интеграл перекрывания между функциями 3d_z² и φ₂. Таблицы, подобные табл. 5.4, называются в математике матрицами.

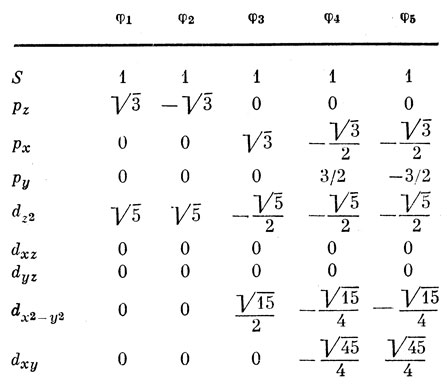
Таблица 5.4. Матрица перекрывания атомных орбиталей фосфора и фтора (в единицах s)

Видно, что две из d-орбиталей совершенно не перекрываются с орбиталями фтора. Они не будут вносить никакого вклада в прочность связей, описываемых гибридными орбиталями (в принятом здесь приближении), так что их можно не рассматривать. Остальные орбитали будут полезны при построении гибридных функций.

Легко видеть, что р_х- и р_y-орбитали напоминают соответственно d_x²-y²- и d_ху-орбитали. Пять оптимальных гибридных функций можно построить из одной s-, трех р- и одной d_z²-орбиталей; эти sр³d-гибридные орбитали уже упоминались ранее. Вместо р_х- и р_y-функций можно использовать d_x²-y² и d_xy, так что получим sрd³-гибридные орбитали. Оптимальные гибридные орбитали должны включать все эти функции. Используя стандартный метод [71], можно получить матрицу перекрывания оптимальных гибридных орбиталей с орбиталями φ₁ ... φ₅ (оптимальными являются, по определению, те гибридные орбитали, которые обеспечивают максимум суммы диагональных элементов этой матрицы); см. табл. 5.5. Из этой таблицы видно, что каждая гибридная функция локализована преимущественно в направлении одного из атомов фтора, так как недиагональные элементы матрицы очень малы. Следует ожидать, что экваториальные связи несколько сильнее, чем аксиальные, потому что гибридные функции χ₃, χ₄ и χ₅, соответствующие экваториальным связям, дают несколько большее перекрывание (2,96S), чем аксиальные гибридные функции χ₁ и χ₂ (2,93S). Однако экспериментальные данные противоречат этому результату, и, как показал Коттон [12], результат получается обратным, если не делается предположение, что интегралы перекрывания пропорциональны значениям угловых функций на линии связей, а производится точный расчет интегралов перекрывания. Однако наша цель была не в том, чтобы изложить детальную теорию связи в молекуле PF₅, а в том, чтобы показать, каким образом можно получить некоторые общие выводы относительно вида гибридных орбиталей.

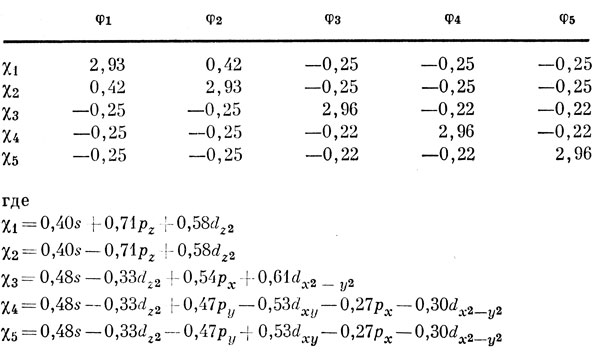
Таблица 5.5. Матрица перекрывания между оптимальными гибридными орбиталями и орбиталями атомов фтора (в единицах s)

Поскольку существуют молекулы PF₅ и SF₆, можно было бы ожидать и существование молекулы ClF₇. Однако атом хлора просто не настолько велик, чтобы удерживать вокруг себя семь атомов фтора на расстоянии, достаточном для возникновения сильной связи (соединение IF₇ существует, вероятно, в форме пятиугольной бипирамиды). Хорошо известно соединение ClF₃. Атом хлора имеет семь электронов в М-оболочке, которые вместе с тремя электронами атомов фтора, дают пять электронных пар, связанных с атомом хлора. Эти пять пар образуют связи, стремящиеся расположиться в виде тригональной бипирамиды, так что отталкивание между электронами различных пар минимально. Оказывается, что три атома фтора занимают оба аксиальных положения и одно из экваториальных, так что молекула имеет форму буквы Т (рис. 5.20).

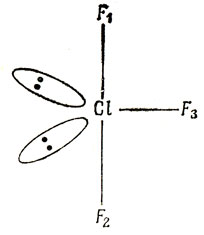
Рис. 5.20. Несвязывающие электроны в ClF₃

Связь в молекулах типа XeF₄ и XeF₆ не сильно отличается от связи в молекулах типа ClF₃ и IF₇, которые также имеют более восьми электронов в валентной оболочке. Соединения инертных газов - не единственные среди тех, для которых нарушено правило октетов. Общее правило, предсказания структуры молекул, подобных ClF₃, которая содержит несвязывающие и связывающие пары электронов, основано на допущении, что две несвязывающие электронные пары отталкиваются друг от друга сильнее, чем связывающая и несвязывающая пары, а последние - сильнее, чем две связывающие пары ^*).

^*) (Анализ структуры молекул, использующий это правило, проводится в работе [63].)