6.2. Вариационный метод и теория возмущений

В квантовой механике мы сталкиваемся с тем, что уравнение Шредингера невозможно решить точно для подавляющего большинства систем, за исключением простейших. Поэтому мы вынуждены удовлетвориться получением приближенных решений этого уравнения и попытаемся сделать их настолько близкими к точным решениям, насколько это возможно. Наиболее общий подход заключается в том, чтобы написать решение в виде разложения по известному набору функций, согласно выражению (6.39), и затем изменять коэффициенты c_i до тех пор, пока не получится наилучшая волновая функция. Существует два общих метода получения приближенных решений волнового уравнения - метод возмущений и вариационный метод.

В методе возмущений исходят из набора собственных функций гамильтониана H°, который приближенно совпадает с истинным гамильтонианом H системы. Собственные функции оператора H представляются в виде разложений по полной системе собственных функций оператора H и коэффициенты находят последовательными приближениями. Например, чтобы получить волновые функции и уровни энергии для атома водорода во внешнем электрическом поле (эффект Штарка), в качестве исходных берутся собственные функции атома водорода в отсутствие поля (они образуют полную систему только в том случае, если включаются как функции связанных состояний, так и функции, соответствующие несвязанным состояниям). Пусть

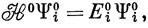
и требуется отыскать соответствующие собственную функцию и собственное значение оператора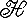

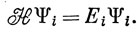
Положим

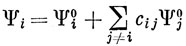
(эту функцию можно нормировать в дальнейшем) и, подставляя равенство (6.42) в выражение (6.41), получим

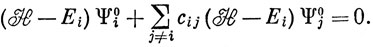
Полный гамильтониан 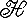представим в виде

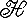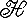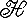= °+ ', (6.44)

где H'- возмущение.

Подставляя равенство (6.44) в выражение (6.43) и используя выражение (6.40), имеем

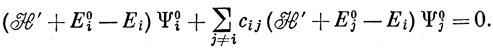
Умножая выражение (6.45) слева на Ψ_i°^*, интегрируя по всему пространству и пользуясь ортонормированностью функций Ψ_i°, получаем

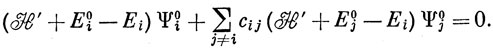
где

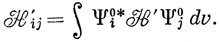
Аналогично, умножая выражение (6.45) слева на Ψ_k^0* (при k ≠ i), находим

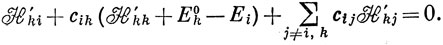
Энергия и коэффициенты представляются в виде разложений

где штрихом отмечены добавки первого порядка по H', двумя штрихами - второго порядка и т. д. Выделим теперь члены из уравнений (6.46) и (6.48), которые имеют одинаковый порядок по H'.

Для членов первого порядка малости из уравнения (6.46) имеем

Таким образом, поправка первого порядка к энергии вычисляется с помощью невозмущенных волновых функций и оператора возмущения.

Члены первого порядка малости в уравнении (6.48) имеют вид

следовательно, поправка первого порядка к коэффициентам равна

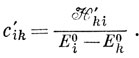
Члены второго порядка малости в выражении (6.46) дают

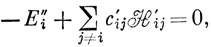
и, используя равенство (6.52), получаем поправку второго порядка к энергии, равную

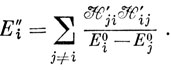
Если Ψ_i⁰ - действительные функции, то H_ji' H_ij' = (H_ij')², но, в любом случае, в силу эрмитовости оператора H', H_ji'H_ij' - действительная неотрицательная величина.

Из выражений (6.52) и (6.54) видно, что поправки первого порядка к коэффициентам и второго порядка к энергии содержат в знаменателе разность энергий, вычисленных с функциями Ψ°; состояния, наиболее близкие по энергии, вносят наибольший вклад в поправку. Поскольку H_ji'H_ij' всегда действительная и неотрицательная величина, состояния с энергией, большей Е_i⁰, уменьшают энергию i-го уровня невозмущенной системы, а с меньшей энергией увеличивают ее.

Соотношения (6.50), (6.52) и (6.54) являются наиболее важными в теории возмущений, так как редко приходится учитывать поправки более высоких порядков. Критерий применимости теории возмущений можно записать в виде

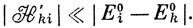
Ясно, что рассмотренная здесь теория непригодна, если существуют вырожденные состояния (например, Е_i⁰ - E_k⁰), потому что в этом случае соответствующие члены в с_ik' и Е_i″ могут обратиться в бесконечность. Однако в этом случае можно применять вариационный метод, который и рассматривается сейчас.

Наиболее важный критерий точности приближенной волновой функции дается вариационной теоремой. Она утверждает, что энергия, вычисленная с приближенной волновой функцией, всегда выше, чем наименьшее собственное значение гамильтониана, т. е. если Θ - приближенная волновая функция, не обязательно нормированная, то

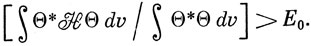
Для доказательства этой теоремы разложим Θ в ряд по собственным функциям оператора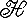

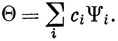
Подставим это разложение в выражение (6.56) и используем ортонормированность функций Ψ_i; тогда нужно доказать ^*)

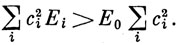
^*) (Мы полагаем здесь, что коэффициенты с действительны, в противном случае c_i² следует заменить на с_i^*c_i. В дальнейшем это допущение делается па протяжении всей главы.)

Это с необходимостью выполняется для наименьшего собственного значения Е₀ оператора 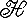так как

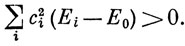
Таким образом, если выбрать волновую функцию, содержащую вариационные параметры, выразить соответствующую энергию через эти параметры и затем минимизировать энергию по отношению к значениям параметров, то можно получить наилучшее приближение к энергии основного состояния, возможное при данном выборе функции. Например, если волновая функция берется в виде

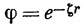
для 1s-орбитали атома Не, то, как будет показано в разд. 9.3, энергия основного состояния атома Не равна

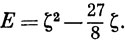
Дифференцируя это выражение по ζ и приравнивая результат к нулю, получим

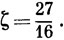
Подстановка этого значения ζ в выражение (6.60) дает наилучшую 1s-орбиталь атома Не, записанную в чисто экспоненциальном виде.

Наиболее обычный путь применения вариационного принципа заключается в следующем: волновая функция представляется как линейная комбинация функций заданного набора, а затем варьируются коэффициенты этой комбинации так, чтобы получить минимальную энергию.

Пусть волновая функция записана в виде линейной комбинации n функций

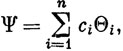
где коэффициенты с_i - вариационные параметры. Тогда

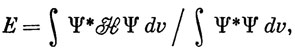
и, подставляя выражение (6.62) в уравнение (6.63), получим

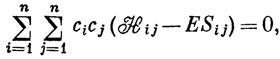
где

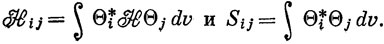
Дифференцируя уравнение (6.64) по c_k при постоянных значениях остальных коэффициентов (напоминаем, что H_ij и S_ij - постоянные), имеем

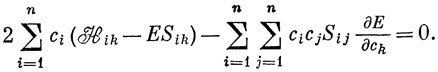
Для минимального значения энергии

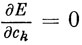
и, следовательно,

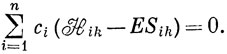
При варьировании каждого из коэффициентов c_k получается уравнение такого же вида, как и уравнение (6.67), т. е. всего n уравнений. Однако система из n линейных уравнений с n неизвестными (коэффициентами с_i) вида (6.67) совместна только в том случае, если определитель, составленный из ее коэффициентов, равен нулю, т. е. ^*)

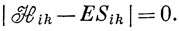
^*) (Например, уравнения

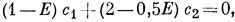
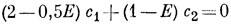
совместны только в том случае, если

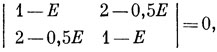
т. е. если (1 - Е)² - (2 - 0,5Е)² = 0 или Е = ±2. Легко видеть, что любое другое значение Е, будучи подставлено в уравнения (а) и (б), дает различные значения c₁/c₂.)

Определитель (6.68), который называют вековым определителем, представляет собой полином степени n относительно энергии Е. Все n корней (значений Е), получающиеся при решении уравнения, соответствуют точкам стационарности интеграла (6.63). Наименьший корень дает наилучшее для данной функции типа (6.62) значение энергии основного состояния. Коэффициенты в этой функции определяются подстановкой наименьшего корня в систему уравнений (6.67) и решением ее обычным путем. При этом решение получается с точностью до постоянного множителя, который определяется из условия нормировки функции. Пример такого вычисления приводится в гл. 12, поэтому подобный расчет здесь не рассматривается.

Можно также показать, что решения системы (6.67) дают не только наилучшую функцию основного состояния, но также и наилучшие функции возбужденных состояний, которые, вообще, возможно получить, аппроксимируя функцию конечной суммой (6.62). При этом необходимо учесть требование ортогональности функций возбужденного состояния к функциям всех состояний с более низкой энергией.

Если функции Θ_i, по которым проводится разложение,являются собственными функциями некоторого гамильтониана H⁰, то они образуют ортонормированный набор и можно написать, что S_ik = δ_ik, H_ik = H_ik' + δ_ikE_k⁰ (используя обозначения, введенные при рассмотрении теории возмущений). Тогда вековое уравнение (6.67) перепишется в виде

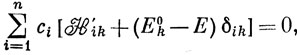
что аналогично выражению (6.46) теории возмущений. Выражения (6.50) и (6.54), дающие поправки к энергии в теории возмущений, можно тогда рассматривать как приближения к точным решениям векового уравнения

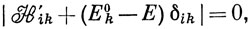
если суммирования проводить не до бесконечности, а только по всем состояниям, включенным в набор, по которому производится разложение.

Если теория возмущений неприменима в том виде, в каком мы рассмотрели ее, в силу существования вырожденных или почти вырожденных состояний у невозмущенной системы, то для вычисления энергий необходимо построить вековой определитель. Теория возмущений для вырожденного случая подробно обсуждается в более полных курсах квантовой механики (см., например, [24]).

Объем работы, возникающей при использовании метода разложения для получения приближенных волновых функций, определяется в основном тем, с какой точностью требуется получить волновые функции и соответствующие энергии; вряд ли надо говорить, что лучше всего взять такой набор исходных функций, для которого сходимость к точной собственной функции является наиболее быстрой.

Значительные упрощения можно сделать в подобных расчетах, если разложение производить по системе собственных функций оператора, который коммутирует с гамильтонианом. Так, например, если Θ₁ и Θ₂ - собственные функции оператора Β, соответствующие различным собственным значениям, и оператор Β коммутирует с оператором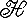

то

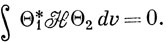
Для доказательства рассмотрим интеграл

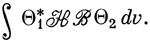
Если

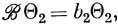
то этот интеграл равен

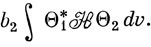
Однако если 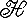и Β коммутируют и Β - эрмитовский оператор, то выражение (6.72) преобразуется в

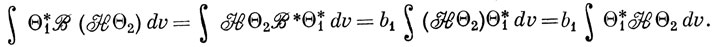
Выражения (6.73) и (6.74) должны совпадать, но если b₁ ≠ b₂, это возможно только в том случае, если интеграл (6.71) равен нулю.

Этот результат чрезвычайно важен, и его использование можно проиллюстрировать на следующем примере. Допустим, что необходимо получить атомные орбитали многоэлектронного атома. Соответствующее разложение для них будет

где функции Θ_i имеют в общем случае вид

Здесь n и ζ - постоянные, которые можно выбрать различными для разных функций Θ_i. Функции Y_lm(θ, φ) - сферические гармоники (3.6), являющиеся, как видно из гл. 9, собственными функциями операторов орбитального момента импульса; значки l и m характеризуют соответствующие собственные значения. Гамильтониан коммутирует с операторами момента импульса (спиновые слагаемые не включены в гамильтониан), поэтому интегралы от гамильтониана, вычисленные для функций с различными значениями момента импульса, обращаются в нуль. Таким образом, интегралы типа (6.71) равны нулю, если Θ₁ и Θ₂ имеют различные квантовые числа l и m. Отсюда следует, что вековой определитель можно разбить на блоки, стоящие на главной диагонали, такие, что каждый из них содержит функции, с одинаковыми квантовыми числами l и m, а недиагональные члены, связывающие блоки с разными l или m, равны нулю. Вековой определитель можно тогда записать в виде произведения определителей более низкого порядка, каждый из которых характеризуется числами l и m, а волновые функции, получающиеся при решении соответствующих уравнений, также характеризуются этими квантовыми числами. Таким образом, именно потому, что операторы момента импульса коммутируют с гамильтонианом, атомные орбитали можно записать в форме (4.3), где сферическая гармоника выделена в виде множителя.

Дальнейшие примеры применения этого правила можно найти в других разделах книги. В гл. 8, в частности, будет показано, как можно использовать симметрию функций для упрощения расчетов, в которых волновые функции ищутся в виде разложений по некоторой системе функций.