
Глава 9. Момент импульса и уровни энергии атома
9.1. Операторы момента импульса
Выясним теперь связь между квантовыми числами l и m атомных орбиталей и моментом импульса электрона и рассмотрим, как трактуется в квантовой механике спин электрона. Далее, на основе этого обсудим уровни энергии атома более подробно, чем это было сделано в гл. 3 и 4.
В классической механике момент импульса относительно точки О определяется векторным произведением L = r × р:
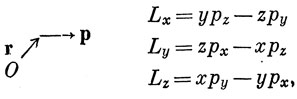
где р - импульс частицы. Чтобы получить наблюдаемые значения момента импульса в квантовой механике, нужно знать соответствующие операторы момента импульса. Построим их по правилу, изложенному в гл. 6 (постулат 2), т. е. заменяя р на
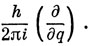
Тогда получим
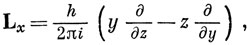
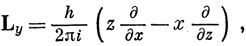
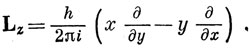
Если перемножить эти операторы, можно увидеть, что они не коммутируют:
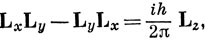
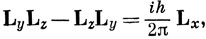
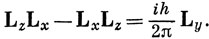
Будет представлять интерес также оператор квадрата момента импульса
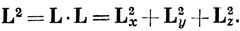
Пользуясь определением (9.2), можно доказать, что L2 коммутирует со всеми операторами проекции момента импульса, т. е.
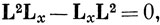
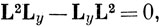
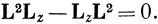
Поскольку операторы проекции орбитального момента импульса не коммутируют между собой, невозможно поставить такой эксперимент, в котором определяются одновременно сами величины Lx, Ly и Lz, а не средние значения их (см. стр. 97). Однако оператор L2 коммутирует со всеми операторами проекций момента импульса, и поэтому можно одновременно измерить квадрат полного момента импульса и значение какой-либо одной из его проекций. Это самое большее, что можно сделать. Обычно принято выбирать волновые функции атома таким образом, чтобы этой проекцией являлась Lz. Если поставить эксперимент для измерения значений L2 и Lz, например налагая магнитное поле в направлении оси z и наблюдая поглощение света атомом, то в этом эксперименте значения проекций Lx и Ly останутся неопределенными. Можно всегда вычислить средние значения операторов Lx и Ly, но вектор L может быть с одинаковой вероятностью направлен как вдоль положительного, так и вдоль отрицательного направления оси x (или оси y), и поэтому средние значения равны нулю.
Поскольку операторы L2 и Lz коммутируют, они имеют общую систему собственных функций Flm, которые определяются уравнениями:
L2 Flm = kl Flm,
Lz Flm = km Flm. (9.6)
Здесь kl и km - постоянные, называемые собственными значениями соответствующих операторов. Если эти соотношения выполняются, то
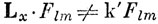
и
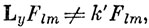
где k' - какая-либо постоянная. Если обратимся теперь к выражениям для операторов проекций момента импульса (9.2) и будем решать уравнения (9.6), то увидим, что функции Flm - сферические гармоники Ylm, определенные в гл. 3 и выражающие зависимость АО от углов. Кроме того, постоянные kl и km находятся из соотношений
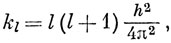
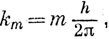
где l = 0, 1, 2, ..., а при данном значении l число m принимает 2l + 1 значений: l, l - 1, ... 0, ..., - (l - 1), - l. Поэтому можно отождествлять целые числа l и m с квантовыми числами, введенными в гл. 3, так что если АО записана в виде комплексной функции (3.9), то электрон на этой орбитали обладает определенными значениями L2 и Lz. Если же используются действительные функции (3.10), то L2 имеет определенное значение, a Lz нет, кроме случаев, когда m = 0.
Если L2 имеет определенное значение
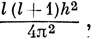
абсолютная величина вектора орбитального момента импульса равна
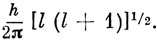
Однако направление этого вектора не фиксировано в пространстве, потому что это потребовало бы одновременного квантования всех трех компонент L.
Можно получить собственные значения оператора момента импульса, не используя определений (9.2) и не решая уравнений (9.6). Если взять в качестве общего определения операторов момента импульса в квантовой механике перестановочные соотношения (9.3) и (9.5), то, пользуясь только этими соотношениями, можно показать, что величины kl и km даются выражениями (9.7). В этом более общем случае, однако, число l может быть либо одним из целых чисел l = 0, 1, 2, ..., либо одним из получелых чисел
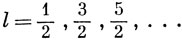
При данном значении l число m снова может пробегать все значения от l до - l, отличающиеся на единицу. Эти результаты справедливы для любых операторов, удовлетворяющих тем же перестановочным соотношениям, что и операторы L2 и Lx, Ly, Lz. Однако для операторов орбитального момента импульса допустимы только целые значения l. Эти утверждения доказаны, например, в книге [24].
В гл. 4 уже указывалось, что электрон обладает собственным (спиновым) моментом импульса. Если предположить, что операторы спинового момента импульса также подчиняются перестановочным соотношениям (9.3) и (9.5), то для одного электрона согласие с экспериментом наблюдается в том случае, когда l берется равным
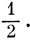
Если
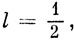
то
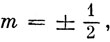
т. е. возможны два новых состояния электрона. Принято описывать их двумя собственными функциями α и β. Обозначая операторы спинового момента символом S и пользуясь соотношениями (9.6) и (9.7), получим
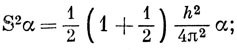
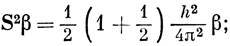
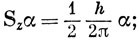
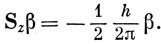
Эти спиновые функции предполагаются ортонормированными:
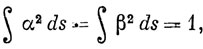
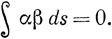
В классической теории магнитный момент находящегося на орбите электрона равен
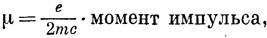
где
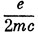
называют гиромагнитным отношением. Это соотношение справедливо и в квантовой механике для орбитального момента импульса, т. е. μz (орбитальный) =
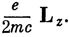
Однако подстановка электронного спинового момента импульса
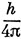
в это выражение дает
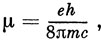
что составляет лишь половину значения, вытекающего из опытов Штерна - Герлаха (а также полученного Уленбеком и Гоудсмитом при исследовании тонкой структуры спектральных линий). Для спинового момента импульса поэтому приходится принять гиромагнитное отношение равным
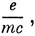
т. е. операторы спинового магнитного момента имеют вид
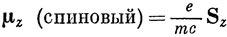
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'