9.2. Уровни энергии атома

Для электрона с номером i в атоме можно ввести операторы спинового и орбитального моментов:

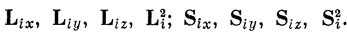
Однако для многоэлектронного атома наблюдаемой величиной является полный момент импульса всех электронов, так как электроны невозможно отличить один от другого. Операторы полного орбитального и полного спинового моментов определяются так:

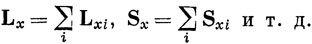
и

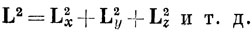
Кроме того, можно определить оператор полного (спинового и орбитального) момента импульса для всего атома:

Каждый из введенных здесь моментов должен удовлетворять квантовомеханическим соотношениям (9.6) и (9.8). Введем обозначения L, M_L, S, M_s, J и M_J для квантовых чисел, характеризующих собственные значения операторов L₂, L_z, S², S_z, J² и J_z соответственно ^*). Например, так как операторы J² и J_z коммутируют, существуют функции F_JM, удовлетворяющие уравнениям

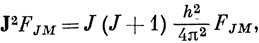
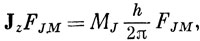
где J - либо целое, либо полуцелое число, а М_J = J, J - 1, ..., -J.

^*) (Квантовое число, имеющее смысл собственного значения оператора J_z, обычно обозначают М, однако мы используем для него обозначение M_J, чтобы подчеркнуть его связь с полным моментом импульса.)

Значение операторов момента импульса в атомной спектроскопии определяется тем, что они коммутируют друг с другом и с оператором Гамильтона. Если какой-либо оператор коммутирует с гамильтонианом, то волновые функции, описывающие систему (собственные функции гамильтониана), могут быть выбраны так, чтобы они были собственными функциями этого оператора. Например, если оператор L² коммутирует с H, то квантовое число L можно использовать для характеристики волновых функций так, чтобы каждая волновая функция соответствовала определенному значению L. Если же оператор L² не коммутирует с H, то волновые функции не характеризуются определенным значением L и могут быть измерены только средние значения орбитального момента. Даже если не известен точный вид волновой функции, можно получить полезные сведения относительно ее свойств, если известны значения соответствующих ей квантовых чисел, связанных с моментом импульса.

В табл. 9.1 приведены перестановочные соотношения между операторами момента импульса и гамильтонианом. Эта таблица построена в соответствии со следующими правилами:

Таблица 9.1. Перестановочные соотношения между операторами момента импульса и гамильтонианом, не содержащим членов, описывающих спин-орбитальное взаимодействие. 'Птичка' означает, что операторы, стоящие в соответствующих строке и столбце, коммутируют

1. Операторы спинового и орбитального моментов действуют на различные части волновой функции, поэтому все операторы L коммутируют со всеми операторами S.

2. Поскольку J_z = L_z + S_z, оператор J_z не коммутирует с операторами L_x, S_y и т. д.

3. Так как J₂ = (L + S)² = L² + S² + 2LS = L² + S² + 2(L_xS_x + L_yS_y + L_zS_z), оператор J² не коммутирует с операторами проекций орбитального и спинового моментов, но коммутирует с операторами L² и S².

4. Если гамильтониан не содержит членов, учитывающих взаимодействие между спиновым и орбитальным движением электронов (эти члены обсуждаются позднее), то гамильтониан коммутирует со всеми операторами полного спинового и полного орбитального моментов. Доказательство можно найти в книге [24].

Волновые функции можно выбрать таким образом, чтобы они были собственными функциями любых коммутирующих между собой операторов. Например, H, L², L_z, S², S_z и J_z - все коммутируют между собой, и поэтому волновые функции выбираются так, чтобы они являлись собственными функциями всех этих операторов; для характеристики волновых функций можно использовать соответствующие квантовые числа L, M_L, S, M_S и M_J. Но, с другой стороны, можно выбрать собственные функции операторов H, L², S², J² и J_z, тогда квантовыми числами будут L, S, J и M_J. Практически проще пользоваться первой из этих двух схем, как в большинстве случаев и поступают. Эту схему называют схемой L - S-связи, или рассел-саундерсовой схемой ^*).

^*) (К типу связи Рассела - Саундерса относятся обе рассмотренные здесь схемы, как LM_LSM_S, так и LSJM_J. Другой предельный случай - связь типа j - j - характеризуется сложением орбитального и спинового моментов каждого электрона в отдельности, дающим набор полных одноэлектронных моментов j₁j₂ ..., которые затем слагаются в полный момент системы J. Существуют также промежуточные случаи и так называемые смешанные типы связей, когда отдельные группы электронов в системе описываются различными типами связей. - Прим. ред.)

Возникает вопрос: как найти возможные значения квантовых чисел полного момента импульса, если известны квантовые числа этого момента для отдельных электронов? Общее правило заключается в следующем: если два оператора момента М₁² и М₂² коммутируют (в качестве М можно брать любой из операторов L, S или J) и если собственное значение М₁² равно

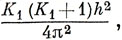
а сооственное значение М₂² составляет

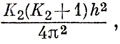
то собственные значения оператора М² (М = М₁ + М₂) равны

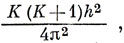
где K = K₁ + K₂, К₁ + К₂ - 1, ... до |K₁ - К₂|. Пользуясь правилом векторного сложения, проектируют меньший из векторов K на больший, как показано на рис. 9.1 для случая, когда К₁ = 3, К₂ = ³/₂.

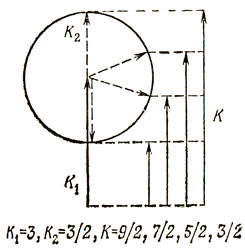
Рис. 9.1. Правило векторного сложения для момента импульса

Предположим, что имеются два электрона, один из которых находится на 2р-орбитали, а другой - на 3р-орбитали. Каковы возможные значения суммарного орбитального момента импульса? Для первого электрона l₁ = 1, для второго l₂ = 1, и возможные значения L таковы:

По аналогии с символикой, принятой для АО, состояния атома обозначают S, P, D, F ..., если полный момент L имеет значения 0, 1, 2, 3, ... соответственнно. В рассматриваемом примере двухэлектронной системы возможны, таким образом, D-, Р- и S-состояния.

Применим это правило к сложению спинов двух электронов. Поскольку s₁ = 1/2 , s₂ = 1/2 (спины первого и второго электронов), то возможными значениями полного спина S будут s₁ + s₂ = 1, s₁ + s₂ - 1 = 0 (= s₁ - s₂). Если S = 1, то M_S = 1, 0, -1. Такое состояние системы из двух электронов называют триплетным состоянием,, потому что возможны три проекции спина. Если S = 0, то M_S = 0, и это есть синглетное состояние. Мультиплетностъ состояния равна 2S + 1, и в обозначении состояния атома она отмечается цифрой слева вверху у символа, обозначающего орбитальный момент. Для электронной конфигурации 2р3р можно получить следующие состояния:

Их принято называть термами. Терм объединяет (2L + 1) (2S + 1) состояний, каждое из которых характеризуется своей парой значений квантовых чисел M_L и M_S.

Различным термам соответствуют разные энергии, потому что для каждого из этих термов энергия отталкивания между электронами на 2р- и 3p-орбиталях различна. Существует правило (его называют правилом Гунда) для определения низшего терма в случае основной (с наименьшей энергией) конфигурации; согласно этому правилу, основной терм имеет наибольшую мультиплетность, а среди термов с одинаковой мультиплетностью более низкая энергия соответствует терму с большим значением L.

Для конфигураций, соответствующих основному состоянию, исключения из этого правила не известны. Однако исключения часто имеют место для возбужденных конфигураций. В разд. 9.6 более подробно обсуждается вопрос об энергии, соответствующей рассел-саундерсовой связи.

Электроны заполненных оболочек (например, s², р⁶, d¹⁰) могут давать только термы ¹S. Таким образом, возможные для данной конфигурации термы определяются только электронами незаполненных оболочек. Если в оболочке может содержаться максимум n электронов, то термы, возникающие при наличии в ней k электронов, такие же, как возникающие при наличии k дырок (т. е. n - k электронов). Таким образом, конфигурация р⁴ приводит к тем же термам, что и р², а конфигурация d³ - к тем термам, что и d⁷ и т. д. (см. задачу 9.4).

Для каждого терма можно определить возможные значения J. Например, терму ³D соответствуют S = 1, L = 2. Возможные значения J в этом случае следующие: 2 + 1, 2 + 1 - 1, 2 - 1, т. е. 3, 2, 1. Если при заданных L и 5 возможны несколько значений J (это имеет место при условии, что L или 5 не равны нулю), каждому терму соответствует несколько уровней, для которых значение J указывается внизу справа у символа терма: ³D₃, ³D₂, ³D₁. Каждый уровень включает 2J + 1 состояний с различными значениями M_J, вырожденных в отсутствие внешнего поля.

Теперь подведем итоги сказанному выше. Для атома с конфигурацией, содержащей незаполненные оболочки, возможны несколько термов, которые отличаются между собой в соответствии с тем, что моменты импульсов отдельных электронов могут складываться по-разному. Различным термам соответствуют разные энергии. Если, например, возбуждать атом Mg из основного состояния ¹S с конфигурацией (1s)² (2s)² (2р)⁶ (3s)² с переходом в первую возбужденную конфигурацию (1s)² (2s)² (2p)⁶ (3s) (3р), то в спектре должны наблюдаться не одна, а две области поглощения, так как для возбужденной конфигурации возможны термы ¹Р и ³Р. Переходу ¹Р ← ¹S соответствует энергия 35050 см^-1, а переходу ³Р ← ¹S - энергия 21900 см^-1.

Если изучается переход ³Р ← ¹S, то при достаточно высокой степени разрешения наблюдается триплет с компонентами 21850, 21870 и 21911 см^-1. Эти три компоненты связаны с переходами на три различных уровня, соответствующие терму ³Р : ³Р₀ ← ¹S, ³P₁ ← ¹S и ³Р₂ ← ¹S соответственно. Расщепление терма ³Р вызвано взаимодействием между спиновым магнитным моментом электронов и магнитным полем, возникающим при движении электронов вокруг ядра. Это спин-орбитальное взаимодействие учитывается путем включения в гамильтониан суммы членов, пропорциональных L_iS_i для каждого электрона (i - номер электрона):

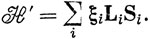
Известно, что для одного электрона, находящегося в центральном поле с потенциалом V(r),

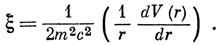
Предполагают, что и в многоэлектронном атоме величины ξ_i могут быть представлены этой же формулой.

Если в гамильтониан включено слагаемое H', то он уже не коммутирует с L², L_z, S² и S_z, и квантовые числа L, M_L, S, M_S перестают быть "хорошими" квантовыми числами. С гамильтонианом коммутирует теперь лишь оператор полного момента, и, строго говоря, имеют смысл лишь квантовые числа J и M_J. Однако расчеты показывают, что энергия спин-орбитального взаимодействия, вычисленная с учетом уравнения (9.17), пропорциональна Z^4*). Для легких атомов расщепление конфигурации на отдельные термы вследствие электронного отталкивания обычно значительно больше, чем дополнительное расщепление термов на уровни, вызванное спин-орбитальным взаимодействием. Поэтому можно утверждать, что, даже если учитывается спин-орбитальное взаимодействие, L и S приближенно являются достаточно "хорошими" квантовыми числами (хотя этого сказать о M_L и M_S нельзя). Это иллюстрируется результатами, приведенными для атома Mg.

^*) (Потенциал пропорционален Z, а водородоподобные функции содержат множитель Z^3/2 в нормировочной постоянной (см. табл. 3.2). Поэтому интеграл вида (6.2), где в качестве Β взят оператор H', пропорционален Z⁴.)

Допустим, что в качестве исходных берется совокупность термов, соответствующих данной конфигурации и характеризующихся квантовыми числами L и S. Считая спин-орбитальное взаимодействие малым возмущением, можно найти в первом порядке теории возмущений [см. формулу (6.50)], что терм с данными L и S расщепляется таким образом, что каждому значению J соответствует отдельный уровень (всего 2L + 1, если L > S, и 2S + 1 при S > L). Относительное расстояние между уровнями можно оценить, если воспользоваться правилом, согласно которому действие возмущения ∑ L_iS_i пропорционально действию возмущения ^*)

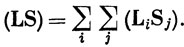
^*) (Доказательство этого утверждения содержится в книге [31] (гл. 5.1).)

Поскольку

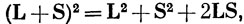
то

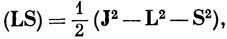
и потому для уровня, характеризующегося определенными значениями J, L и S, в первом порядке теории возмущений энергия спин-орбитального взаимодействия пропорциональна выражению

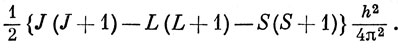
Из этой формулы можно получить правило интервалов Ланде, согласно которому расстояние между двумя уровнями с разными J пропорционально большему из двух значений J (см. задачу 9.6).

Атом Fe в основном состоянии имеет конфигурацию (4s)² (3d)⁶, и среди различных возможных термов наиболее низкая энергия соответствует терму ⁵D. Тогда вследствие спин-орбитального взаимодействия этот терм расщепляется, как показано в табл. 9.2. В последнем столбце таблицы все числа были бы одинаковы, если бы правило Ланде было точным. Малость отклонения их от постоянного значения оправдывает возможность учета спин-орбитального взаимодействия в первом порядке теории возмущений.

Таблица 9.2. Расщепление терма ⁵D атома Fe

Если терм возникает из конфигурации с менее чем наполовину заполненной оболочкой (например, р²), то при спин-орбитальном расщеплении уровень с меньшим значением J имеет меньшую энергию (второе правило Гунда). Эту картину расщепления называют нормальным мультиплетом. Если же конфигурация состоит из оболочки, заполненной более чем наполовину, то наименьшая энергия соответствует уровню с наибольшим J, и в этом случае мультиплет называют обращенным (см. табл. 9.2), а энергия убывает с ростом J. Для оболочек, заполненных наполовину, в первом порядке теории возмущений спин-орбитального расщепления термов вообще не получается; экспериментально наблюдается очень слабое расщепление, обусловленное эффектами второго порядка.

Для тяжелых атомов энергии спин-орбитального взаимодействия довольно велики, но, если электроны находятся на орбиталях примерно одинаковой протяженности, схема Рассел - Саундерса все же является довольно хорошим исходным приближением. Например, в атоме Ва (6s6p) энергии таковы: ³Р₀ = 12266, ³Р₁ = 12636, ³Р₂ = 13515, ¹Р₁ = 18060 см^-1. Однако, если электронное взаимодействие значительно меньше спин-орбитального, что имеет место для электронов, находящихся на орбиталях с сильно отличающимися протяженностями, то имеет место случай j - j-связи. Каждый электрон обладает определенными l и s, которые, складываясь, дают два или одно значение j (если l = 0, возможно лишь одно значение j). Для того чтобы получить результирующее значение J, полные моменты j отдельных электронов складываются в соответствии с законом сложения моментов. Например (сравните с энергиями для атомов Mg и Ва), для атома Si(3s)²3p6s энергии термов ³Р₀, ³P₁, ³P₂ и ¹P₁ равны 59221, 59273, 59506, 59636 см^-1 соответственно. Для 3p-электрона возможные значения j равны ³/₂ и ¹/₂, а для 6s-электрона - только ¹/₂. Сложение моментов j = 3/2 и j = 1/2 дает J = 2, 1, а сложение j = 1/2 и j = 1/2 дает J = 1, 0. На рис. 9.2 показан переход от чистой рассел-саундерсовой схемы связи к чистой j - j-связи для конфигурации sp. Движению слева направо соответствует рост отношения энергии спин-орбитального взаимодействия к энергии взаимодействия между электронами.

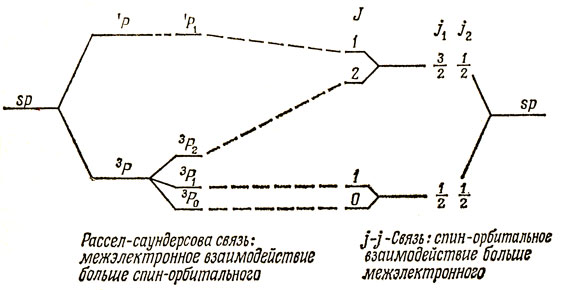
Рис. 9.2. Переход от рассел-саундерсовой связи к j - j-связи