9.3. Влияние принципа Паули

Правило векторного сложения, используемое при вычислении возможных значений полного момента импульса, не содержит никаких ограничений, возникающих при учете принципа Паули. Как уже говорилось, в частности, полный спин системы из двух электронов может быть равен 1 или 0, но если оба электрона занимают одну и ту же орбиталь, то принцип Паули запрещает состояние со спином S = 1, так как на одной орбитали могут быть два электрона только с противоположными спинами. Рассмотрим термы, возникающие из конфигурации р². Еще раньше было сказано, что из конфигурации рр (например, 2р3р) возникают шесть термов ³D, ¹D, ³Р, ¹Р, ³S, ¹S. Покажем, что три из этих термов несовместимы с принципом Паули. В табл. 9.3 перечислены всевозможные способы распределения двух электронов в р-подоболочке. Стрелка направлена вверх, если спиновое состояние электрона описывается функцией α, и - вниз, когда оно выражается функцией β. Здесь выбрана комплексная форма р-орбиталей, так чтобы им соответствовали определенные значения m.

Таблица 9.3. Возможные способы распределения двух электронов в р-подоболочке

Обратимся сначала к состоянию с наибольшим значением M_L, т. е. к состоянию (1), для которого M_L = 2 (как видно из табл. 9.3, состояния с большим значением M_L невозможны). Поскольку при этом M_S = 0, оно относится к терму ¹D, которому соответствуют всего пять состояний с M_L = 2, 1, 0, -1, -2. Чтобы выделить их, нужно отыскать по таблице состояния с этими значениями M_L и M_S = 0. Все пять компонент терма ¹D имеют L = 2, S = 0. Из таблицы видно, что к терму ¹D относятся состояния (1), (15), одно из состояний (3) и (4), одно из состояний (12) и (13) и одно из состояний (7), (8) и (9).

Из оставшихся состояний выберем снова состояние с наибольшим значением M_L, а если таких состояний несколько, то возьмем состояние также и с наибольшим M_S. Этому соответствует состояние (2). Поскольку для него M_L = 1 и M_S = 1 и среди оставшихся нет состояний с более высокими M_L и M_S, оно относится к терму ³Р. Для терма ³P L = 1, S = 1, и потому он имеет девять компонент с M_L = 1, 0, -1 и M_S = 1, 0, -1. Остальные восемь компонент можно выбрать в соответствии с табл. 9.3.

Таким образом, из 15 возможных состояний 14 уже рассмотрены. Следовательно, остается только одно из состояний (7), (8) или (9), для которых M_L = 0, M_S = 0. Поэтому оставшийся терм должен быть ¹S, ибо он имеет только одну компоненту.

Принцип Паули, таким образом, допускает только термы ¹D, ³P и ¹S для конфигураций р², что составляет лишь половину всех термов, возможных для конфигурации pp. Данные спектроскопии подтверждают, что действительно возможны лишь термы ¹D, ³P и ¹S, а также дают другие результаты, свидетельствующие в пользу принципа Паули.

Для конфигурации р² возможны три функции с M_L = 0, M_S = 0. Одна из них соответствует терму ¹D, другая - терму ³Р, а третья - терму ¹S. Чтобы найти явный вид волновых функций для каждого из термов, необходимы дополнительные уравнения.

Пользуясь перестановочными соотношениями для операторов момента импульса, можно показать, что для собственной функции операторов L₂ и L_z, такой, что

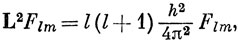
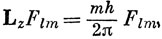
справедливы следующие соотношения (см. [24]):

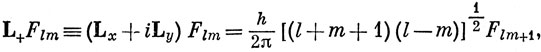
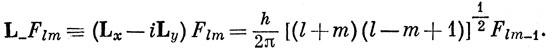
Оператор L₊, действуя на функцию F_lm, переводит ее в собственную функцию с тем же значением l и большим на единицу значением m; оператор L_- понижает на единицу значение m, оставляя l неизменным. Эти операторы называют операторами сдвига. Они позволяют по известной собственной функции операторов L² и L_z с заданными l и m построить собственные функции, соответствующие тому же значению l и замене m на m + 1 или m - 1. Соотношения, подобные уравнению (9.21), справедливы также для операторов S и J. Соотношения (9.21) связывают также между собой фазы волновых функций F_lm-1, F_lm, F_lm+1. Для собственных функций орбитального момента импульса эти выражения дают правильный знак только в том случае, если взять F_lm = Y_lm (m ≤ 0), F_lm = (-1)^m Y_lm (m > 0)i где Y_lm - сферические гармоники, определенные по уравнению (3.6). В качестве примера рассмотрим спиновые состояния двух электронов, находящихся на разных орбиталях. Обозначим электроны числами 1 и 2 и выпишем все четыре возможные спиновые функции двух электронов:

      α(1)α(2)   α(1)β(2)   β(1)а(2)   β(1)β(2) 
MS =     1           0         0          -1

Действуя оператором S_-(1) на функцию α(1), получим [полагая в выражении (9.21)

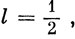
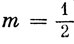
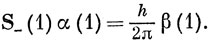
Следовательно,

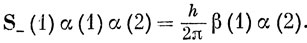
Аналогично оператор S_-(2) переводит функцию α(1) α(2) в α(1) β(2). Функция α(1) α(2) должна быть F₁₁-компонентой триплетного состояния (для нее S = 1, M_S = 1). Если требуется построить F₁₀-компоненту триплетного состояния, для которой М_S = 0, достаточно подействовать на F₁₁ оператором S_- = S_-(1) + S_-(2). Тогда, согласно выражению (9.21), получаем

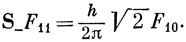
Однако из соотношения (9.22) следует, что

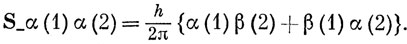
Следовательно,

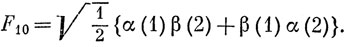
Действуя на F₁₀ оператором S_-, находим

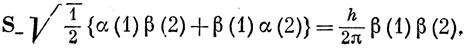
т. е. компоненту триплета F_1-1, для которой M_S = -1, как и следовало ожидать на основе определения оператора S_-.

Для того чтобы построить волновую функцию синглетного состояния, надо взять такую линейную комбинацию функций, соответствующих M_S = 0, которая ортогональна функции (9.23) триплетного состояния. Пусть

Тогда, согласно соотношениям (9.9), получаем

если а = -b. Таким образом, нормированная функция синглетного состояния имеет вид

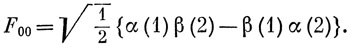
Если нужно найти собственные функции операторов L² и S² для конфигурации р², поступим следующим образом. Функция (1) (табл. 9.3) является компонентой терма ¹D с M_L = +2. Соответствующую функцию можно написать (используя обозначения разд. 7.1) в виде |ψ₁αψ₁β|, где ψ₁ - p-орбиталь с m = 1. Если на эту функцию действовать оператором L_-, можно получить функции с M_L = 1, 0, -1, -2. Функция (2) относится к терму ³Р с M_L = 1, M_S = 1, и ее также не трудно написать. Действуя на нее оператором S_-, находим функции с M_L = 1, M_S = 0, -1. Действуя же на полученные функции оператором L_-, получим остальные шесть компонент терма ³Р. Наконец, чтобы построить волновую функцию терма ¹S, надо воспользоваться условием ортогональности ее уже построенным компонентам термов ¹D и ³Р.