9.4. Атомные спектры

В этой книге мы очень коротко рассмотрим вопросы спектроскопии, ограничиваясь лишь теми вопросами, которые имеют непосредственное отношение к электронной структуре атомов и молекул. Уровни энергии электронов в атомах - это не единственное, что можно получить, изучая атомные спектры. Изменения в спектрах, создаваемые лигандами в комплексе металла, позволяют судить о силе связи между лигандами и металлом, а также о геометрии расположения лигандов.

Монохроматический свет может поглощаться атомом при условии сохранения полной энергии. Таким образом, если атом находится в состоянии с энергией Е₀, то должно существовать и состояние с энергией Е₁, такое, что [см. соотношение (1.2)]

Однако при поглощении света должны соблюдаться также условия, называемые правилами отбора. В случае атома эти правила требуют, чтобы квантовые числа полного момента импульса при переходах изменялись следующим образом:

причем переход из состояния с J = 0 в состояние с J' = 0 запрещен. В схеме Рассела - Саундерса, где L и S - достаточно "хорошие" квантовые числа, имеют место правила отбора ΔS = 0, ΔL = 0, ±1. Если, кроме того, электронный переход сводится к возбуждению электрона с одной орбитали на другую (обычно такое приближение вполне удовлетворительно), то для такого одноэлектронного перехода должно соблюдаться правило Δl = ±1.

Существует еще одна характеристика, которую можно использовать для строгой классификации атомных состояний - это четность состояния. Поскольку атом обладает центром симметрии, волновые функции должны быть или неизменны или менять знак при инверсии в центре симметрии. Состояния, функции которых не изменяются при инверсии, называют четными; состояния, функции которых меняют знак в результате инверсии, называют нечетными и отмечают значком (о) справа вверху у символа терма. Чтобы найти четность состояния, надо перемножить четности всех занятых электронами орбиталей (произведение двух орбиталей с одинаковой четностью дает функцию четного состояния, а с разной - нечетного) или, что проще, вычислить сумму всех орбитальных моментов l отдельных электронов. Например, основное состояние атома углерода ³Р возникает из четной конфигурации 2s²2p². Конфигурация 2s2p³, соответствующая возбужденному состоянию, приводит к возникновению нечетного терма ³Р⁰. Согласно правилу Лапорта, при поглощении света разрешены переходы лишь между состояниями с разной четностью.

Уровни энергии атома в отсутствие внешнего поля 2J + 1-кратно вырождены. Если бы это было не так, то направление вдоль оси z существенно отличалось бы, например, от направлений вдоль осей х или y ^*). Если же атом помещают во внешнее поле, то (2J + 1)-кратное вырождение снимается.

^*) (Эквивалентность различных направлений при отсутствии внешнего поля связана со свойством изотропии пространства. - Прим. перев.)

Внешнее магнитное поле расщепляет уровень на 2J + 1 компоненту, каждая из которых характеризуется определенным значением M_J, если магнитное поле направлено вдоль оси z. Если это расщепление мало по сравнению со спин-орбитальным, то имеет место эффект Зеемана, при котором каждый уровень расщепляется на 2J + 1 равноотстоящие компоненты. Расстояние между компонентами равно

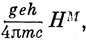
где Н^M - напряженность магнитного поля и

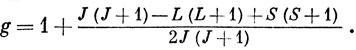
Если расщепление, создаваемое магнитным полем, сравнимо по величине со спин-орбитальным, то получаем так называемый эффект Пашена - Бака, для которого расположение энергетических уровней более сложно.

При действии на атом внешнего электрического поля наблюдается эффект Штарка. В однородном поле, направленном вдоль оси z, каждый уровень расщепляется таким образом, что компоненты с различными

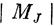
имеют различные энергии. Взаимодействие такого поля с атомом (или молекулой) выражается через электрический дипольный момент. В случае атома дипольный момент сам возникает благодаря полю, причем наведенный дипольный момент связан с напряженностью поля через поляризуемость атома α (см. разд. 18.1):

Из этого выражения следует, что энергии взаимодействия электрического поля с атомом соответствует в гамильтониане слагаемое вида ^*)

^*) (Формулы (9.28 и (9.29) содержат макроскопический коэффициент а, явный вид которого определяется из квантовомеханических расчетов; эти формулы имеют классический характер и не представляют собою операторов соответствующих величин. К тому же при получении выражения (9.29) необходимо учесть работу образования самого диполя, что вносит в окончательное выражение коэффициент

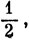
т. е.

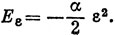
- Прим. ред.)

Отсюда сразу видно, что при изменении направления поля на противоположное эта энергия не изменяется. Изменение направления поля эквивалентно переходу из состояния с заданным М_J в состояние с -M_J, а следовательно, эти состояния и при наличии поля имеют одинаковые энергии. Для атома водорода эта простая картина эффекта Штарка несколько усложняется. В этом случае орбитали с одним и тем же значением n, но разными l относятся к вырожденному состоянию, и поэтому величина штарковского расщепления уровня зависит от напряженности поля линейно, а не квадратично. Поскольку оператор H^Е не зависит от спиновых переменных, то добавка его в гамильтониан при отсутствии спин-орбитального взаимодействия (схема Рассела - Саундерса) приведет только к снятию вырождения для состояний с разными

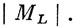
Таким образом, вид штарковского расщепления энергетических уровней зависит от относительной величины спин-орбитального взаимодействия и взаимодействия с электрическим полем, подобно тому как в случае эффекта Зеемана - Пашена - Бака он зависит от относительной величины спин-орбитального взаимодействия и взаимодействия с магнитным полем. Эффект Штарка представляет собой простейший случай действия электрического поля на атом. В гл. 13 рассматривается действие неоднородных полей, создаваемых лигандами, входящими в комплекс металла.