9.5. Атом гелия

Атом гелия - простейший пример многоэлектронного атома, для которого невозможно получить точное решение уравнения Шредингера. На примере атома гелия можно испытать методы, применяемые для получения приближенных решений этого уравнения. Будет видно также, что в этом случае удается получить результаты, точность которых совпадает по крайней мере с точностью эксперимента.

Сначала рассмотрим основное состояние атома. В рамках одноэлектронного приближения можно считать, что оба электрона занимают 1s-орбиталь и имеют противоположные спины. Волновую функцию запишем в виде [см. выражение (7.6)]

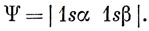
Согласно выражению (6.13), гамильтониан имеет вид

где электроны обозначены цифрами 1 и 2, а координаты их показаны на рис. 9.3.

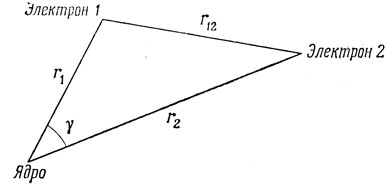
Рис. 9.3. Система координат для атома Не

Выясним, в поле какого потенциала находится электрон 1. Для этого воспользуемся результатом классической электростатики, согласно которому потенциал, создаваемый сферически распределенным зарядом вне сферы, такой же, как если бы весь заряд был сосредоточен в центре, а внутри сферы (в шаровой полости с тем же центром) потенциал равен некоторой постоянной ^*).

^*) (Авторы ошибочно утверждают, что эта постоянная равна полному заряду, и в соответствующей формуле С - 2/r₁ для потенциала считают С = 1. На самом деле С = 4π ∫_R0^R r ρ(r) dr, где R₀ - радиус полости; R - радиус электронного облака; ρ(r) - плотность заряда. - Прим. перев.)

Если электрон 1 находится далеко от ядра, то электрон 2 вероятнее всего можно обнаружить вблизи ядра, и поэтому электрон 1 находится в поле потенциала - 2-1/r₁. Электрон, движущийся в поле такого потенциала, описывается 1s-волновой функцией атома водорода (см. табл. 3.3), которая в атомных единицах имеет вид

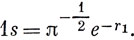
Если электрон 1 попадает в область, очень близкую к ядру, то потенциал поля равен С - 2/r₁; в нем превалирует член -2/r₁, и 1s-волновая функция при таком потенциале равна

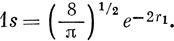
Ясно, что усредненный потенциал, действующий на электрон 1, будет заключен между крайними двумя значениями, соответствующими полному экранированию ядра электроном 2 (на больших расстояниях) и отсутствию такого экранирования (при малых расстояниях). Соответствующая этому усредненному потенциалу волновая функция, по-видимому, может быть записана в виде

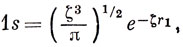
где ζ - эффективный заряд ядра, заключенный между 1 и 2.

Оптимальное значение ζ можно определить вариационным методом, минимизируя энергию. Вычислим интеграл

с 1s-орбиталями в виде (9.34) ^*). Стоящий под интегралом справа от оператора H слэтеровский определитель запишем в явном виде [см. выражение (7.4)]:

^*) (dτ = dυds - элемент объема, включающий как спиновые, так и пространственные переменные.)

Поскольку гамильтониан симметричен относительно перестановки электронов, оба слагаемых дают один и тот же вклад в энергию; поэтому возьмем лишь одно из них и результат умножим на 2. Однако эта двойка сокращается с произведением нормировочных постоянных обоих слэтеровских определителей, так что, расписывая подробно также и определитель, стоящий слева от гамильтониана, получаем

Изложенный здесь прием упрощения интегралов, содержащих слэтеровские определители, является общим: достаточно взять лишь произведение диагональных элементов определителя, стоящего справа от оператора, и отбросить нормировочные постоянные у обоих слэтеровских определителей.

Проинтегрируем теперь по спиновым переменным. Тогда в силу ортогональности функций α и β ненулевым оказывается лишь интеграл, содержащий слева от оператора H функцию 1sα(1) 1sβ(2). Подставляя явный вид оператора H, находим

Заметив, что 1s-орбиталь является собственной функцией оператора (- 1/2 ∇² - ζ/r) с собственным значением -ζ²/2 [см. соотношение 3.19)], получим

В соответствие с тем, что оператор в фигурных скобках состоит из трех слагаемых, интеграл разбивается на три интеграла. Интеграл, содержащий 1/r₁, упрощаем, интегрируя по координатам электрона 2. Аналогично преобразуем интеграл, содержащий 1/r₂; очевидно, что оба полученных результата совпадают. Тогда

Среднее значение 1/r, вычисленное с водородоподобными 1s-функциями (с эффективным зарядом ζ), равно ζ (см. задачу 3.4). Таким образом, остается вычислить лишь двухэлектронный интеграл, представляющий собой энергию взаимного отталкивания электронов. Это осложняется множителем 1/r₁₂ в подынтегральном выражении. Однако можно воспользоваться формулой (см. рис. 9.3).

и разложить 1/r₁₂ в ряд (см. [24]):

где Y_lm - сферические гармоники, определенные по уравнению (3.6), а r<, r> - меньшее или большее из чисел r₁ и r₂. Хотя 1/r₁₂ разлагается в бесконечный ряд, после интегрирования по углам, в силу ортогональности сферических гармоник с разными l остаются слагаемые лишь с теми значениями l, которые входят в электронные плотности, содержащиеся под интегралом. В рассматриваемом случае электронные плотности 1s² сферически симметричны (угловая часть содержит только гармонику Y₀₀), и из всей бесконечной суммы сохранится лишь одно слагаемое (с l = 0):

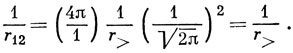
Разобьем интеграл по r₁ и r₂ на два интеграла:

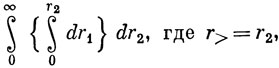
и

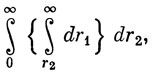
где r_> = r₁,

и, интегрируя, можно показать, что двухэлектронный интеграл равен

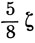
(см. задачу 9.12).

В результате для энергии получаем

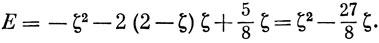
Применим теперь вариационный принцип. Дифференцирование по ζ дает

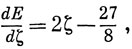
так что минимум энергии отвечает ζ = 1,6875. Этому значению ζ соответствует Е = -2,8476 ат. ед. (-77,483 эв) По данным спектроскопии энергия, необходимая для вырывания обоих электронов из атома Не, равна -79,000 эв и вычисленное нами значение энергии отличается от экспериментального на 1,5 эв, что составляет 1,9%.

Энергия, получающаяся при использовании 1s-орбитали, с учетом экранирования ядра

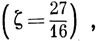
на 3 эв ниже энергии, соответствующей 1s-орбитали без учета экранирования (ζ = 2). Это довольно значительное понижение. Однако и водородоподобная функция, учитывающая экранирование, не является той наилучшей 1s-орбиталью, которую можно было бы получить, используя метод ССП, предложенный Хартри и Фоком. Наилучшее значение энергии, получающееся при использовании функции типа (9.30) без наложения каких-либо ограничений на аналитический вид 1s-орбитали, равно -77,866 эв, т. е. дальнейшее понижение энергии составляет только 0,383 эв. Однако все же остается довольно значительное расхождение между вычисленным и экспериментальным значениями энергии.

Это различие объясняется несколькими причинами. Во-первых, предполагалось, что масса ядра бесконечно велика по сравнению с массой электрона. Поэтому при переходе от атомных единиц к электронвольтам надо использовать не массу электрона, а приведенную массу электрона и ядра

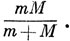
Однако это меняет результат всего лишь на 0,017% (0,013 эв). Во-вторых, в гамильтониане не были учтены релятивистские эффекты, проявляющиеся, например, в спин-орбитальном взаимодействии. Для тяжелых атомов они могут быть существенны, но для атома Не они вносят поправку в энергию лишь порядка 0,004 эв. Основной причиной расхождения является то обстоятельство, что волновая функция (9.30), не будучи точным решением уравнения Шредингера, совершенно не учитывает корреляции электронов. Энергия корреляции оказывается равной примерно 1,1 эв ^*).

^*) (Энергию корреляции обычно определяют как разность между энергией, вычисленной по методу ССП Хартри - Фока, и точным значением энергии, полученным в нерелятивистском приближении.)

Корреляция между двумя частицами определяется следующим образом. Пусть Р(r₁, r₂) - вероятность нахождения первой частицы в точке r₁ и второй в точке r₂; пусть, далее, Р(r₁) - вероятность обнаружения частицы 1 в точке r₁, усредненная по всем положениям частицы 2, а Р(r₂) - вероятность нахождения частицы 2 в точке r₂, усредненная по всем положениям частицы 1. Тогда при отсутствии корреляции для системы из двух частиц справедливо соотношение

Иначе говоря, положение любой из частиц зависит только от усредненного положения другой.

Решение многоэлектронного уравнения Шредингера должно учитывать корреляцию между электронами. Среди различных типов волновых функций, обладающих этим свойством, наиболее естественными являются те, которые явно содержат расстояние между электронами. Функция такого типа впервые была предложена Хиллераасом для атома гелия в 1929 году. Он предложил взять в качестве волновой функции произведение е^{-ζ(r₁+r₂)} (т. е. функции, не учитывающей корреляцию электронов) на полином по степеням r₁, r₂ и r₁₂. Простейшая среди функций такого вида

дает для энергии значение, отличающееся от экспериментального лишь на 0,34 эв. При использовании полинома, содержащего четырнадцать членов, различие уменьшается до 0,002 эв. В последнее время применяют полиномы с еще большим числом членов, и вычисленные значения энергии практически совпадают с экспериментальными.

Расчеты, проведенные Хиллераасом и другими для атома гелия, принципиально важны: они показывают, что уравнение Шредингера правильно описывает двухэлектронные атомы. Оно, по-видимому, справедливо и для многоэлектронных атомов и молекул, хотя в этих случаях его нельзя решить точно. К сожалению, функция типа Хиллерааса для систем, содержащих более двух электронов, приводит к огромным математическим трудностям. В этих случаях для учета электронной корреляции обычно применяют метод наложения конфигураций, который обсуждается в гл. 12.

Теперь остановимся кратко на возбужденных состояниях атома гелия, чтобы пояснить понятие обменной энергии. В одноэлектронном приближении мы полагаем, что первому возбужденному состоянию соответствует конфигурация (1s)(2s), при которой возможны термы ¹S и ³S. Выпишем полностью соответствующие этим термам волновые функции

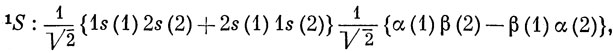
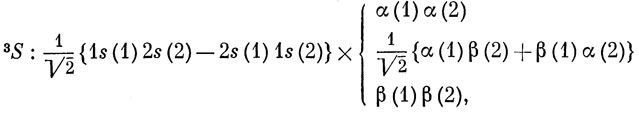
или, используя сокращенные обозначения определителей,

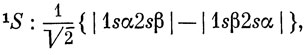
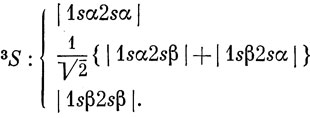
Для триплетного состояния имеются три компоненты (соответствующие M_s = 1, 0, -1). Спиновые волновые функции для синглетного и триплетного состояний были получены в разд. 9.4 [см. выражения (9.23) и (9.24)]. Все функции (9.47) удовлетворяют требованию антисимметрии (см. разд. 7.1). Синглетная функция имеет антисимметричную спиновую часть, и потому ее пространственная часть должна быть симметричной относительно перестановки электронов. Для триплетной функции спиновая часть симметрична, а пространственная антисимметрична относительно перестановки электронов. Обе функции построены с учетом неразличимости электронов, т. е. вероятность нахождения электрона 1 на 1s-орбитали такая же, как и для электрона 2.

Вычислим теперь энергию терма ³S. Для этого можно взять любую из трех функций [см. выражение (9.47)], например |1sα2sα|, так как в отсутствие внешнего поля все они должны давать одну и ту же энергию. Действуя таким же образом, как и при расчете основного состояния, приходим к следующему выражению для энергии [см. выражение (9.36)]:

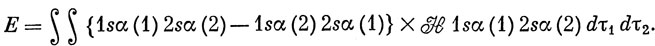
В отличие от основного состояния, после интегрирования по спинам остаются оба слагаемых в функции, стоящей слева от оператора, поскольку теперь оба электрона имеют одинаковые спиновые функции. Теперь вместо выражения (9.37) получаем

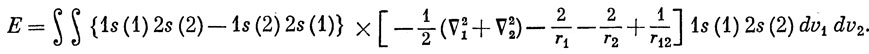
Как и в расчете основного состояния, разобьем гамильтониан на одноэлектронные и двухэлектронные операторы и воспользуемся взаимной ортогональностью 1s- и 2s-орбиталей:

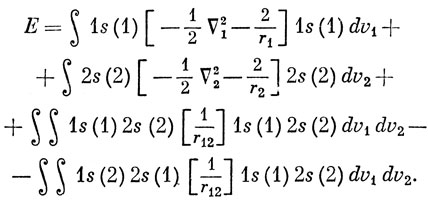
Первые два слагаемых в уравнении (9.50) представляют собой энергии 1s- и 2s-орбиталей в поле ядра атома гелия, а третье - энергию отталкивания электронных зарядов с плотностями 1s² и 2s². Последнее слагаемое не имеет аналога в выражении (9.39); оно соответствует взаимодействию двух электронных зарядов с плотностями 1s(1) 2s(1) и 1s(2) 2s(2). Это последнее слагаемое называют обменной энергией. Оно понижает энергию и происходит оттого, что в волновой функции ³S-состояния учтена тождественность электронов. С другой стороны, в выражение для энергии основного состояния не входит обменный член, так как электроны в основном состоянии имеют противоположные спины. Для основного состояния энергия получается такой же, если вместо антисимметризованного произведения (определителя) использовать обычное произведение 1sα(1) 1sβ(2).

Если, действуя аналогично, вычислить энергию возбужденного состояния ¹S, то оказывается, что отличие ее от уравнения (9.50) - лишь в знаке перед обменным интегралом. Величину синглет-триплетного расщепления можно получить из спектроскопических данных; она составляет 6400 см^-1 (0,79 эв).

Если предполагать, что 1s- и 2s-орбитали одинаковы как в синглетном, так и в триплетном состояниях (это вполне разумное предположение), то это синглет-триплетное расщепление равно удвоенному значению обменного интеграла. Обменные интегралы всегда значительно меньше, чем соответствующие кулоновские (например, в атоме гелия кулоновский интеграл, вычисленный с 1s- и 2s-орбиталями, равен примерно 7 эв, что почти в двадцать раз больше величины обменного интеграла). Это связано с тем, что электронные плотности, содержащиеся в обменном интеграле (например, 1s2s), не есть действительные плотности, которые везде неотрицательны, а являются так называемыми переходными плотностями, которые в различных точках могут быть как положительными, так и отрицательными, причем ∫ 1s2s dυ = 0 в силу условия ортогональности.

Обсудим теперь вопрос о корреляции электронов в синглетном и триплетном состояниях, возникающей в силу принципа Паули. Согласно толкованию волновой функции, Ψ² имеет физический смысл плотности вероятности. Чтобы найти плотность вероятности, зависящую лишь от пространственных координат электронов, надо проинтегрировать Ψ² по спиновым переменным. В результате получим функцию Р(r₁, r₂). Для нахождения функции Р(r₁) нужно произвести усреднение, т. е. проинтегрировать еще по координатам электрона 2; проделав все эти процедуры, получим (см. задачу 9.13)

где знак плюс соответствует синглетному, а знак минус - триплетному состоянию. Для обычного произведения 1s (1) 2s (2), не удовлетворяющего принципу Паули, получается, что Р(r₁, r₂) = Р(r₁) Р(r₂).

Если разность Р(r₁, r₂) - Р(r₁) Р(r₂) положительна, то вероятность обнаружения электрона 1 в точке r₁, а электрона 2 в точке r₂ больше, чем это могло быть при отсутствии корреляции [т. е. в расчете, где вероятность дается произведением Р(r₁) Р(r₂)]. Говорят, что в этом случае корреляция положительна. Как для синглетного, так и для триплетного состояния первое слагаемое в уравнении (9.51) положительно, если один электрон находится в области, где функция (1s² - 2s²) положительна, а другой - в области, где эта функция отрицательна. Эти области показаны на рис. 9.4. Второй член в уравнении (9.51) по-разному влияет на корреляцию для синглетного и триплетного состояний: для синглетного состояния корреляция, обусловленная этим членом, положительна, если оба электрона находятся в областях, где знаки функций (1s2s) одинаковы; для триплетного же состояния корреляция положительна при условии, что оба электрона находятся в областях, в которых функции (1s2s) имеют разные знаки.

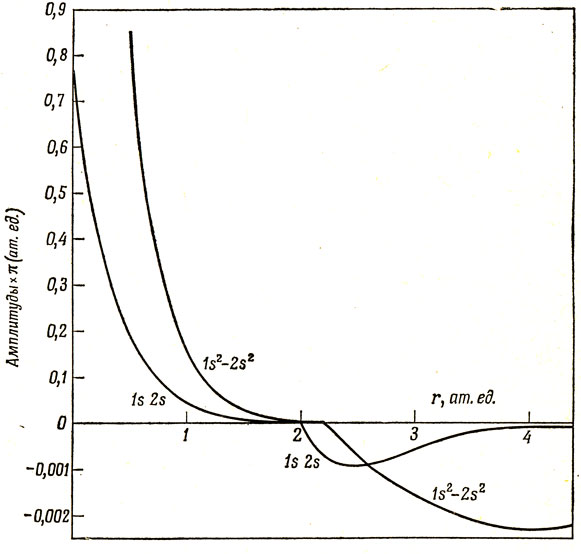
Рис. 9.4. Электронные плотности, определяющие корреляцию электронов в синглетном и триплетном состояниях

Грубо говоря, для синглетного состояния характерно стремление электронов быть ближе друг к другу, а для триплетного - дальше, чем при отсутствии учета корреляции. Эта тенденция проявляется в обменной энергии. Поэтому Линнет предлагает называть обменную энергию спин-корреляционной энергией.