
Глава 10. Метод молекулярных орбиталей и его применение в теории электронной структуры двухатомных молекул
10.1. Молекулярный ион водорода
Метод молекулярных орбиталей в теории электронной структуры молекул есть распространенный на молекулы метод атомных орбиталей *). Предполагается, что электроны в молекуле находятся на орбиталях, охватывающих все ядра в молекуле. Для построения волновой функции основного состояния молекулы распределяют все ее электроны по МО с наименьшей энергией, учитывая ограничение, налагаемое принципом Паули, согласно которому на одной орбитали не может находиться больше двух электронов. Этот способ совершенно аналогичен принципу построения, использованному для объяснения атомной структуры (см. гл. 4).
*) (Метод МО впервые применялся Гундом, Малликеном и Леннард-Джонсом (1927-1929 гг.).)
Чаще всего в методе МО применяют приближение ЛКАО для построения МО. Вблизи ядра электрон находится в поле потенциала, создаваемого в основном этим ядром: поле, обусловленное другими ядрами молекулы, в этой области сравнительно мало. Поэтому вблизи ядра МО должна быть близка к АО соответствующего атома. Учитывая это, предполагают, что разумное приближение к МО во всех точках пространства можно получить, беря линейную комбинацию атомных орбиталей, относящихся ко всем атомам в молекуле. Пусть φν - некоторая АО. Тогда МО представляют в виде
ψ = ∑ν cν φν, (10.1)
где коэффициенты cν подлежат определению. Если в это разложение включить достаточно большое число АО, то, вычисляя коэффициенты разложения на основе вариационного принципа, можно получить довольно хорошее приближение к истинной МО. Однако, как будет видно позднее, даже если включать небольшое число АО и, следовательно, пользоваться для МО весьма грубым приближением, удается получить ряд очень полезных качественных результатов.
В конце настоящей главы кратко рассматриваются некоторые другие виды МО, записанные в эллиптических координатах и пригодные для двухатомных молекул. В гл. 15 обсуждаются МО, построенные для модели свободных электронов и используемые для описания сопряженных систем. Однако в общем случае используются только МО, построенные в приближении ЛКАО.
Рассмотрим сначала простейшую молекулу - ион H2+. Молекулярный ион водорода играет такую же роль в теории молекул, как атом водорода - в теории атома, так как для иона H2+ в приближении Борна - Оппенгеймера электронное волновое уравнение может быть решено точно. Однако мы не будем сейчас останавливаться на точном решении, а построим МО для иона H2+ в приближении ЛКАО, которые послужат нам основой для рассмотрения двухатомных гомоядерных молекул.
Наименьшему значению энергии в атоме водорода соответствует 1s-орбиталь. Поэтому можно ожидать, что соответствующая наименьшей энергии молекулярная орбиталь H2+ вблизи ядер совпадает с 1s-AO и в приближении ЛКАО она может быть представлена в виде
ψ = са1sа + сb1sb, (10.2)
где ядра обозначены буквами а и b.
Соответствующая функции (10.2) электронная плотность вероятности равна
ψ2 = ca2 (1sa)2 + cb2 (1sb)2 + 2cacb (1sa1sb). (10.3)
Поскольку атомы в H2+ неразличимы, плотность вероятности нахождения электрона около каждого из ядер должна быть одной и той же; это выполняется только в том случае, если
ca2 = cb2. (10.4)
Существуют лишь две орбитали, удовлетворяющие этому условию:
са = сb ψg = Ng (1sa + 1sb), cа = - cb ψu = Nu (1sa - 1sb), (10.5)
где Ng, Nu - нормировочные постоянные. На рис. 10.1 эти орбитали представлены схематически. Функции (10.5) получены из соображений симметрии молекулы; к этому же результату можно было бы прийти, пользуясь более формальными методами теории групп. Символы g и и приняты в теории групп и означают, что орбиталь симметрична (g) или антисимметрична (и) по отношению к инверсии в центре симметрии.
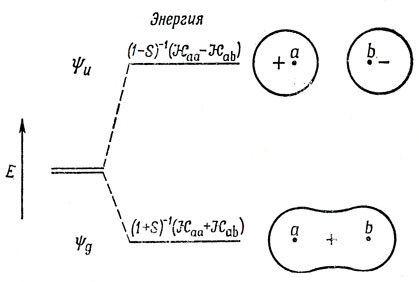
Рис. 10.1. Молекулярные орбитали H2+
Для построенных нами двух орбиталей плотности вероятности равны
ψg2 = Ng2 (1sa2 + 1sb2 + 21sa1sb),
ψu2 = Nu2 (1sa2 + 1sb2 + 21sa1sb). (10.6)
Условие нормировки этих орбиталей дает
∫ ψg2 dυ = Ng2 ∫ (1sa2 + 1sb2 + 21sa1sb) dυ = 1,
∫ ψu2 dυ = Nu2 ∫ (1sa2 + 1sb2 + 21sa1sb) dυ = 1. (10.7)
Введем общепринятое обозначение для интеграла перекрывания
S = ∫ 1sa1sb dυ. (10.8)
Предполагая АО нормированными, получим
Ng2 (2 + 2S) = 1,
Nu2 (2 - 2S) = 1. (10.9)
В гл. 5 обсуждалась качественно роль интеграла перекрывания и отмечалось, что, грубо говоря, он характеризует силу ковалентной связи. Используя явный вид водородной 1s-AO (табл. 3.3)
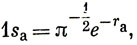
получаем для интеграла перекрывания
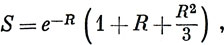
где R - выраженное в атомных единицах межъядерное расстояние. Следует отметить, что в выражение (10.11) входит множитель e-R. Произведение (1sа1sb) называют плотностью перекрывания. Она имеет наибольшее значение там, где функции 1sa и 1sb перекрываются сильнее всего, т. е. в области между ядрами. Из соотношений (10.6) видно, что плотность перекрывания входит со знаком плюс в ψg2 и со знаком минус в ψu2. Поэтому в области между ядрами плотность ψg2 больше, чем плотность электронного облака, распределенного поровну между обоими ядрами (т. е. 1sa + 1sb), а плотность ψu2 меньше этой величины.
Из простых электростатических соображений ясно, что электрон на орбитали ψg обладает меньшей энергией, чем на орбитали ψu, так как в области между ядрами, где суммарное поле обоих ядер велико, плотность ψg2 больше плотности ψu2. Чтобы получить точные энергии этих орбиталей, нужно вычислить для каждой из них интеграл
E = ∫ ψHψ dυ. (10.12)
Подставляя выражения (10.5) и (10.9) в уравнение (10.12), имеем
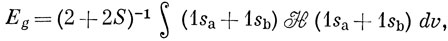
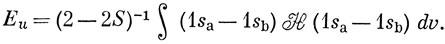
Введем обозначения
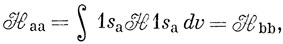
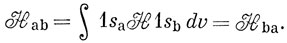
Тогда
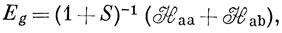
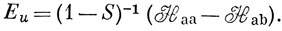
Электронный гамильтониан для иона H2+ (в атомных единицах) имеет следующий вид:
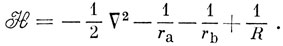
Можно считать, что Hаа представляет собой энергию атома водорода (а), возмущенного полем протона (b), и эта величина близка к энергии свободного водородного атома (за исключением области малых значений R). Интеграл вида Hаb обычно называют резонансным интегралом. Он представляет собой энергию электронного заряда, распределенного с плотностью перекрывания в поле притяжения обоих ядер *). Hab - отрицательная величина, и поэтому энергия Eg ниже, а энергия Еu выше, чем энергия атома водорода в поле протона. ψg называют связывающей молекулярной орбиталью, a ψu - разрыхляющей.
*) (Наличие в гамильтониане оператора кинетической энергии и энергии отталкивания ядер не укладывается в данное здесь толкование резонансного интеграла. - Прим. ред.)
Можно получить несколько более наглядные выражения для энергии, воспользовавшись тем, что 1s-орбиталь удовлетворяет уравнению Шредингера для атома водорода:
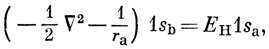
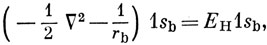
где ЕH - энергия водородной 1s-AO. Тогда выражение (10.16) можно представить в виде
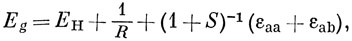
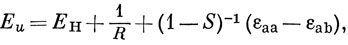
где
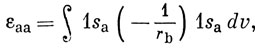
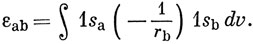
Если вычислить интеграл (10.20), используя явный вид (10.10) 1s-орбитали, получим
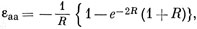
εаb = - е-R(1 + R). (10.21)
Видно, что эти интегралы зависят от межъядерного расстояния R следующим образом: при больших значениях R, еаа изменяется как
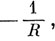
а еаb пропорционально е-R (т. е. изменяется так же, как интеграл перекрывания). Энергия отталкивания ядер, равная
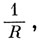
компенсирует почти полностью еаа; поэтому можно сказать, что именно из-за интеграла еаb происходит понижение энергии в состоянии ψg и повышение ее в состоянии ψu по сравнению с энергией системы, состоящей из протона и атома водорода (эти рассуждения нельзя считать правильными при малых значениях R). Кривые потенциальной энергии для состояний ψg и ψu иона H2+ изображены на рис. 10.2.
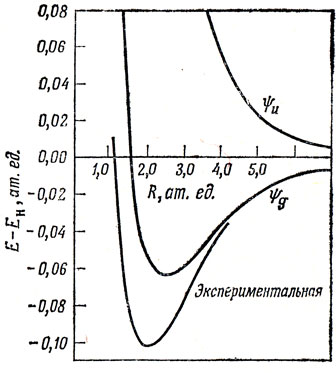
Рис. 10.2. Кривые потенциальной энергии для H2+
Вычисленная таким образом энергия связи H2+ составляет около 60% от экспериментального значения. В конце настоящей главы обсуждаются некоторые более точные расчеты, выполненные по методу МО; здесь же качественно рассматриваются электронные структуры молекулы Н2, а также двухатомных молекул с одинаковыми ядрами, образованные элементами второго периода (от Li2 до F2).
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'