10.2. Молекулярные орбитали гомоядерных двухатомных молекул

Указывалось, как из двух перекрывающихся друг с другом 1s-AO можно построить две МО. Очевидно, что аналогичная ситуация возникнет и в том случае, если перекрываются две 2s-орбитали: связывающей будет орбиталь (2s_a + 2s_b), разрыхляющей - орбиталь (2s_a - 2s_b). Общая форма этих орбиталей такая же, как и для их 1s-аналогов, за исключением того, что 2s-AO имеют узел вблизи ядра.

При перекрывании 2р-АО можно построить шесть МО. Взяв 2p-орбитали, направленные вдоль линии, соединяющей ядра (это направление примем за ось z), навстречу друг другу, получаем связывающую МО (2p_za + 2р_zb) и разрыхляющую МО (2p_za - 2p_zb) (см. рис. 10.3). Кроме того, имеются 2р-орбитали, направленные перпендикулярно к оси молекулы, например вдоль направления оси х. Из них также можно построить связывающую орбиталь (2р_ха + 2р_хb) и разрыхляющую орбиталь (2р_xa - 2p_хb), как это показано на рис. 10.3. Поскольку оси x и y совершенно эквивалентны, молекулярные орбитали (2р_yа + 2р_уb) и (2р_уа - 2р_уb) в силу симметрии соответствуют той же энергии, что и построенные из 2р_х-атомных функций.

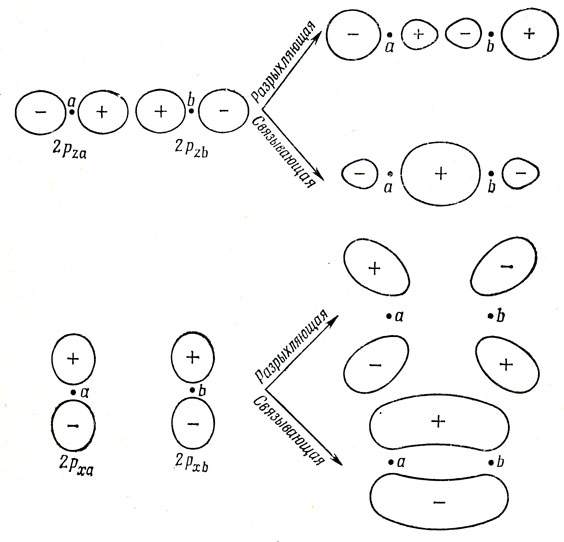
Рис. 10.3. Молекулярные орбитали гомоядерных двухатомных молекул, построенные из 2р-атомных орбиталей

О характере МО можно судить по распределению соответствующей электронной плотности: если в области между ядрами плотность увеличивается, орбиталь - связывающая, если же уменьшается, орбиталь - разрыхляющая.

Молекулярные орбитали гомоядерных двухатомных молекул можно характеризовать свойствами симметрии и значением проекции момента импульса на ось молекулы (фактически классифицировать по НП групп симметрии С_∞υ или D_∞h) так же, как это делается для АО. Значки l и m для АО связаны с орбитальным моментом, причем для каждого значения l возможны 2l + 1 значений m, а соответствующие (2l + 1) АО относятся к вырожденному состоянию. Однако двухатомная молекула обладает более низкой симметрией, чем атом. Воспользуемся аналогией между симметрией двухатомной молекулы и симметрией атома, помещенного в аксиальное электрическое поле, когда для атома наблюдается эффект Штарка (см. стр. 170). При наличии внешнего поля (2l + 1)-кратное вырождение снимается, и АО характеризуются только значением квантового числа m, которое определяет величину составляющей момента импульса электрона вдоль направления электрического поля. Молекулярные орбитали двухатомных молекул характеризуют аналогичным квантовым числом λ, которое определяет проекцию орбитального момента электрона на ось молекулы. Важно уяснить, что квантовое число λ подобно квантовому числу m, а не l.

Орбитали двухатомных молекул можно записать в виде

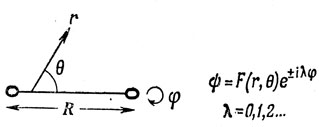
Это выражение следует сопоставлять с уравнением (3.5), записанным для атома, где благодаря более высокой симметрии функция F(r, θ) в свою очередь разбивается на множители, один из которых зависит только от r, а другой - только от θ. Проекция момента импульса на ось молекулы равна

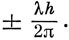
За исключением случая, когда λ = 0, орбитали (10.22) соответствуют двукратно вырожденным состояниям, отличающимся знаком проекции момента на ось молекулы (напомним, что в случае эффекта Штарка орбитали с + m и -m также имеют одинаковую энергию).

Орбитали обозначаются в соответствии со значением λ следующим образом:

              λ = 0, 1, 2, 3, ... 
Тип орбитали      σ, π, δ, φ, ...

Значок, характеризующий значение проекции момента импульса, употребляется для характеристики орбиталей в двухатомных молекулах, как с одинаковыми, так и с разными ядрами. Однако гомоядерные двухатомные молекулы имеют более высокую симметрию (D_∞h), чем гетероядерные молекулы (С_∞υ); поэтому орбитали гомоядерных молекул можно классифицировать дополнительно по их поведению при инверсии в центре симметрии. В табл. 10.1 приведены характеристики МО, полученных в соответствии с их свойствами, показанными на рис. 10.1 и 10.3.

Таблица 10.1. Характеристики МО, построенных из 1s-, 2s- и 2р-АО для гомоядерной двухатомной молекулы

Далее, вводят значок, аналогичный главному квантовому числу АО и нумерующий орбитали в порядке увеличения соответствующей им энергии. Например, орбиталь (1s_a + 1s_b) обозначают 1σ_g, (1s_a - 1s_b) - 1σ_u, (2s_a + 2s_b) - 2σ_g, (2p_za + 2p_zb) - 3σ_g и т. д. Орбитали гетероядерных двухатомных молекул, не обладающих центром инверсии, обозначаются просто 1σ, 2σ, 3σ и т. д. В другом способе обозначения МО, принятом в данной книге, используется символика АО, в которые переходит МО при диссоциации молекулы: σ_g1s, σ_u1s, σ_g2s, σ_u2s и т. д.

Энергия МО определяется двумя величинами: типом АО, из которых она построена, и перекрыванием между этими АО. Например, σ_g1s- и σ_u1s-орбитали имеют гораздо более низкую энергию, чем орбиталь σ_g2s; энергия 1s-AO значительно ниже энергии 2s-AO. Аналогично энергия σ_g2s-орбитали ниже энергии σ_g2р-орбитали, так как, за исключением атома водорода, энергия 2s-AO значительно ниже энергии 2р-АО. Кроме того, при не слишком малых расстояниях между ядрами две 2s-орбитали и две 2p_z-орбитали перекрываются значительно сильнее, чем две 2р_х- или две 2р_у-орбитали. Отсюда следует, что различие в энергии между связывающей и разрыхляющей π-орбиталями меньше, чем между связывающей и разрыхляющей σ-орбиталями. На основе приведенных здесь соображений можно ожидать, что МО располагаются по энергии следующим образом:

Однако 2s- и 2р-АО не столь сильно отличаются по энергии, чтобы их можно было рассматривать как невзаимодействующие. Действительно, когда для объяснения направленной валентности было введено понятие гибридизации (гл. 5), то основанием для этого послужило приближенное равенство энергий 2s- и 2р-АО.

Если 2s- и 2р-АО довольно близки по энергии, то σ-МО, полученные из АО L-оболочки (n = 2), должны быть представлены как комбинация 2s- и 2р_z-орбиталей:

Пользуясь теорией возмущений [см. выражение (6.54)], можно заключить, что взаимодействие 2s- и 2р_z-орбиталей (оно имеет место, так как орбитали 2s_a и 2р_zb перекрываются) понижает энергию первых двух σ-орбиталей этой группы (σ_g2s и σ_u2s) и повышает энергию двух других орбиталей σ_g2p и σ_u2p. При увеличении различия в энергиях 2s- и 2р-АО роль этого взаимодействия уменьшается: для элементов второго периода оно уменьшается при переходе от молекулы Li₂ к молекуле F₂; для более легких молекул этого ряда 2s - 2р-взаимодействие "поднимает" σ_g2р-орбиталь (мы используем это обозначение, хотя оно содержит и некоторую примесь 2s-функций) над π_u2р-орбиталью и приводит к следующему расположению:

Такое расположение МО по энергии наблюдается для всех гомоядерных двухатомных молекул, образованных элементами второго периода, кроме O₂ и F₂; в этих же молекулах орбитали π_u2р и σ_g2p заполнены, и поэтому расположение их по энергии оказывается существенным лишь при рассмотрении возбужденных состояний. Изучение электронного спектра молекулы 02 показывает, что первая возбужденная электронная конфигурация образуется при переходе π_u2р → π_g2p, а не при переходе σ_g2p → π_g2p, т. е. орбиталь σ_g2p имеет более низкую энергию, чем орбиталь π_u2р. Однако если не рассматривать возбужденные состояния, то порядок расположения орбиталей по энергиям [выражение (10.25)] позволяет объяснить свойства симметрии основного состояния всех гомоядерных двухатомных молекул, образованных элементами второго периода, и их положительных ионов столь же успешно, как это удается сделать при выявлении свойств симметрии основных состояний элементов на основе расположения по энергиям АО (гл. 4 и 9). В табл. 10.2 приведены электронные конфигурации, соответствующие основному состоянию гомоядерных двухатомных молекул от Н₂ до F₂ и некоторых положительных молекулярных ионов.

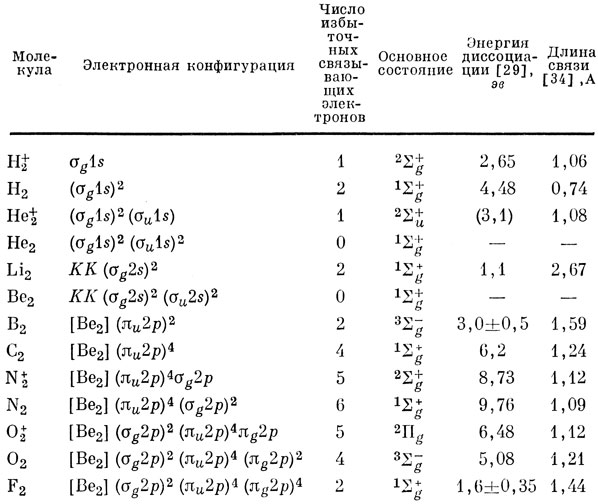
Таблица 10.2. Основные состояния гомоядерных двухатомных молекул (до F₂ включительно)

Бэллик и Рамсей [2] показали, что ¹∑_g⁺-состояние молекулы С₂ лежит ниже состояния (π_u2р)³ (σ_g2p)¹³П_u. которое раньше считали основным, примерно на 0,1 эв.

Символ KK означает, что при равновесном расстоянии между ядрами 1s-орбитали слабо перекрываются, так что их можно рассматривать как несвязывающие (не участвующие в образовании связи).

Значение энергии диссоциации иона Не₂⁺ взято из книги [34], но оно не очень надежно.

Прочность связи зависит, грубо говоря, от того, насколько число электронов на связывающих орбиталях превышает число электронов на разрыхляющих. Так, энергия диссоциации молекулы Н₂ примерно вдвое больше энергии диссоциации иона Н₂⁺, а последняя почти совпадает с энергией диссоциации Не₂⁺. Молекула Не₂ имеет два связывающих и два разрыхляющих электрона и поэтому в основном состоянии не стабильна; существуют, правда, некоторые возбужденные состояния, энергия диссоциации которых на атомы (один в основном, другой в возбужденном состоянии) положительна. Если количество связывающих и разрыхляющих электронов одинаково, то эффект разрыхления всегда превышает эффект связывания, поэтому, например, молекула Ве₂ также не стабильна.

Наиболее прочна связь в молекуле N₂, где число связывающих электронов на шесть больше, чем число разрыхляющих (в структурной формуле это отражается тремя валентными штрихами N ≡ N). Если один электрон вырывается из молекулы N₂, связь становится слабее, а длина связи увеличивается. В молекуле O₂ имеются четыре избыточных связывающих электрона, причем наиболее слабо связан электрон, находящийся на разрыхляющей орбитали π_g2p. Поэтому в молекулярном ионе O₂⁺ связь короче (и прочнее), чем в молекуле O₂.

Состояние атома в целом характеризуют квантовыми числами полного спинового и полного орбитального моментов. Аналогичным образом определяют и состояния двухатомных молекул, задавая значение полного спинового момента и проекции полного орбитального момента на ось молекулы. Как и для атомных состояний, мультиплетность (2S + 1) обозначают числом слева вверху у символа, характеризующего терм. Проекцию полного орбитального момента на ось молекулы обозначают большими греческими буквами в соответствии со следующим правилом:

  ∑ λ = 0, 1, 2, 3, ... 
Символ  ∑, Π, Δ, Φ, ...

Электронную конфигурацию, при которой каждая из орбиталей полностью занята или совсем свободна и нет вырожденных орбиталей, заполненных лишь частично, называют состоянием с заполненными оболочками; такие состояния относятся к типу ¹∑. При этом число электронов со спиновой функцией а равно числу электронов со спиновой функцией β; кроме того, одинаково также число электронов, имеющих проекцию момента импульса

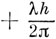
и

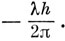
Таким образом, основные состояния молекул Н₂, Li₂, C₂, N₂ и F₂ являются ¹∑-состояниями.

Симметрия состояния молекулы по отношению к инверсии (это свойство относится лишь к гомоядерным двухатомным молекулам) получается путем перемножения четностей функций отдельных электронов в соответствии с правилом g × g = u × u = g; g × u = u. Состояния, нечетные относительно инверсии (u-состояния), наблюдаются только для молекул с нечетным числом электронов на u-орбиталях (например, Не₂⁺).

Существует еще одна операция симметрии для двухатомных молекул, которая не рассматривалась: любая плоскость, содержащая ось молекулы, является плоскостью симметрии, и волновые функции могут быть симметричны или антисимметричны по отношению к отражению в этой плоскости. Все σ-орбитали симметричны относительно этого отражения, и для характеристики их поведения при этой операции симметрии не используют какого-либо специального значка, так как он не дал бы ничего нового. Двукратно вырожденные орбитали π, δ, ... и т. д. всегда можно выбрать таким образом, чтобы одна из каждой пары была симметрична, а другая - антисимметрична относительно отражения в заданной плоскости симметрии; поэтому для этих орбиталей также нет смысла вводить специальное обозначение, определяющее их поведение при отражении в плоскости, проходящей через ось молекулы. То же самое можно сказать и по поводу двукратно вырожденных Π-, Δ-, Φ, ... -состояний молекулы в целом: всегда можно одну компоненту выбрать симметричной, а другую - антисимметричной. Только для ∑-состояний приходится указывать поведение функции при отражении в плоскости. Символ ∑ как раз и указывает, что число электронов с проекцией момента импульса

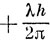
и

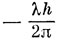
одинаково. Однако возможно ∑-состояние с незаполненной оболочкой, которое может быть симметричным или антисимметричным относительно отражения в плоскости симметрии. Поясним это на следующем примере.

Пусть два электрона занимают две вырожденные π-орбитали, а суммарная проекция их орбитального момента равна нулю. Тогда возможны два распределения электронов по орбиталям соответственно с волновыми функциями [см. выражение (10.22)]:

где e^+iφ (1) означает, что электрон с номером 1 находится на орбитали, соответствующей проекции момента + h/2π, R (1, 2) - не зависящая от углов φ часть волновой функции. Чтобы учесть неразличимость электронов, необходимо взять волновые функции в виде

Пусть R - операция отражения в проходящей через ось молекулы плоскости, от которой отсчитывается угол φ. Тогда при операции R следует заменить φ на -φ, так что

Функция Ψ₊ не изменяется при операции R, и соответствующее состояние обозначают ∑⁺. Функция Ψ_- изменяет знак, и, следовательно, описывает ∑^--состояние. Для электронных конфигураций с заполненными оболочками возможны лишь ∑⁺-состояния; конфигурация, содержащая незаполненные оболочки, например (π_u2р)², может давать как ∑⁺-, так и ∑^--состояния.

Две из молекул, приведенных в табл. 10.2, имеют заполненные наполовину π-оболочки. Для таких электронных конфигураций возможны несколько состояний в зависимости от взаимного расположения спиновых и орбитальных моментов двух электронов. Это аналогично случаю атома с незаполненными оболочками, и мы получим возможные состояния молекул с незаполненными оболочками тем же способом, как это было сделано для p²-конфигурации атома. Можно разместить электроны по π-орбиталям с учетом принципа Паули следующим образом (ср. с табл. 9.3):

Распределение электронов с ∑λ = 2 должно быть отнесено к Δ-состоянию, и, так как полный спин равен нулю, получим ¹Δ-состояние. Учитывая распределение с ∑λ = - 2, можно видеть, что ¹Δ-состояние вырождено двукратно (а не пятикратно, как ¹D-состояние атома). Четыре распределения отвечают ∑λ = 0, и они должны быть отнесены к ∑-состояниям. Очевидно, что три из них соответствуют триплету, так как ∑ m_s = 1, а четвертое является синглетным ¹∑-состоянием. Триплетная спиновая функция двух электронов симметрична относительно их перестановки [см. выражение (9.23)]; следовательно, для выполнения принципа Паули пространственная часть ее (для ³∑-состояния) должна быть антисимметрична относительно перестановки электронов (так как полная функция должна быть антисимметрична). Отсюда следует, что пространственная часть функций ³∑-состояния должна быть функцией Ψ_- [см. выражение (10.26)], т. е. описывать состояние ³∑^-.

Синглетная спиновая функция антисимметрична относительно перестановки электронов; соответствующая пространственная функция симметрична, и поэтому получаем ¹∑⁺-состояние.

Таким образом, конфигурация π² гомоядерных двухатомных молекул приводит к состояниям ¹Δ_g, ³∑_g^-, ¹∑_g⁺. В согласии с правилом Гунда состояние с наиболее низкой энергией является триплетным, а энергия состояния ¹Δ_g ниже энергии состояния ¹∑_g⁺.

По данным спектроскопии основным состоянием молекул O₂ и В₂ является ³∑_g^--состояние. Триплетность также означает, что эти молекулы должны быть парамагнитными. Простое объяснение природы основного состояния этих молекул является одним из блестящих успехов метода МО. Значительно труднее объяснить структуру этих молекул, пользуясь методом ВС (см. гл. 11).