10.4. Гетероядерные двухатомные молекулы

Для гетероядерных двухатомных молекул коэффи циенты ЛКАО в приближении МОЛКАО нельзя найти на основании симметрии. Их определяют методом, основанным на вариационном принципе. Поскольку вопрос об определении орбитальных энергий молекулы и соответствующих коэффициентов ЛКАО чрезвычайно важен, ниже выводятся необходимые для этого уравнения при использовании, однако, более простого, но менее строгого метода, чем предложенный в гл. 6.

Предположим, что МО, представленные в приближении ЛКАО в виде

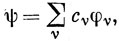
являются собственными функциями некоторого гамильтониана Н, т. е.

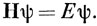
Здесь не рассматривается явный вид оператора Н, следует отметить только, что он является одноэлектронным оператором (так как ψ - одноэлектронная функция), который, строго говоря, определяется однозначно лишь для молекулы с одним электроном (например, H₂⁺): в этом случае Н есть фактический электронный гамильтониан молекулы. Отложим обсуждение этого вопроса до конца настоящей главы, ограничиваясь здесь утверждением, что Н содержит оператор кинетической энергии электрона и усредненный эффективный потенциал, действующий на выделенный электрон и создаваемый всеми ядрами и остальными электронами молекулы.

Подставляя выражение (10.27) в уравнение (10.28), получаем

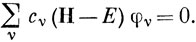
Чтобы определить коэффициенты c_ν, умножим выражение (10.29) слева на одну из АО, например φ_μ (или комплексно сопряженную с ней, если рассматриваются комплексные функции), и проинтегрируем по всему трехмерному пространству. Это дает

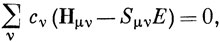
где

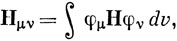
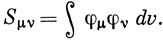
Уравнение типа (10.30) выводится для каждой из АО, включаемых в линейную комбинацию (10.27). Если число таких орбиталей равно n, то получаем систему n уравнений относительно n коэффициентов c_ν. Определитель системы этих уравнений называют вековым (секулярным); эта система уравнений имеет ненулевое решение только в том случае, если вековой определитель порядка n равен нулю, т. е. [см. уравнение (6.68)]

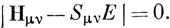
Раскрывая определитель, получаем уравнение степени n относительно Е, которое имеет n корней. Решения этого уравнения есть энергии МО, которые могут быть образованы линейными комбинациями n АО.

Пусть Е_r - одно из решений уравнения (10.33). Чтобы найти коэффициенты в МО ψ_r, имеющей это значение энергии, подставляем Е_r вместо Е в систему (10.30) и, решая ее обычным методом, находим отношение коэффициентов. Абсолютные величины коэффициентов определяются из условия нормировки.

Уравнения (10.30) имеют в точности такой же вид, как и уравнения (6.67), полученные в результате применения вариационного принципа к линейной комбинации атомных функций с неизвестными коэффициентами. Отсюда следует, что МО, найденные путем решения системы (10.30), являются наилучшими в смысле вариационного принципа, даже если в сумме (10.27) мы взяли бы малое число слагаемых - слишком малое для того, чтобы считать r собственной функцией оператора Н.

В качестве примера расчета по методу МО, в котором используются полученные выше уравнения, рассмотрим молекулу LiH (гидрид лития). Произведем только грубую оценку встречающихся в расчете интегралов, однако это все же позволит нам выделить качественные особенности МО гетероядерных двухатомных молекул. Основному состоянию атома лития соответствует конфигурация (1s)² 2s; атом водорода содержит один электрон, находящийся на 1s-орбитали. Предположим, что связь возникает благодаря делокализации 2s-электрона лития и 1s-электрона водорода в молекуле LiH. В простейшем варианте метода МО эта делокализация вводится построением МО как линейных комбинаций функций 2s_Li и 1s_H. Для того чтобы сделать функцию более гибкой, включим в нее также 2рσ-орбиталь атома лития ^*). Будем предполагать, что 1s-орбиталь лития не участвует в образовании связи, так как она не перекрывается с водородной 1s-орбиталью сколько-нибудь значительно. Это предположение означает, по существу, что задача о молекуле LiH рассматривается как двухэлектронная.

^*) (Используем обозначение 2рσ для р-орбитали, ориентированной вдоль линии связи; это общепринятое обозначение позволяет устранить необходимость указывать выбор координатных осей.)

Возьмем σ-МО в виде

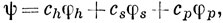
где φ_h - водородная 1s-орбиталь; φ_s - 2s- и φ_р - 2рσ-орбитали лития. Каро и Олсен [43, 44] вычислили все необходимые интегралы с этими атомными функциями. Воспользуемся их результатами. При равновесном значении длины связи 3 ат. ед. (1,6 А) интегралы перекрывания равны ^*)

^*) (Изменим знак использованной Каро и Олсеном 2s-функции для того, чтобы все интегралы перекрывания были положительны.)

Рассмотрим теперь интегралы, содержащие гамильтониан. Предположим сначала, что рассматривается молекула LiH⁺. Можно было бы утверждать в этом случае, что внешний электрон движется в поле, потенциал которого создается зарядом протона, равным +1, зарядом ядра атома лития, равным +3, и двумя 1s-электронами лития. Пусть V (1s²) - потенциал поля, создаваемого 1s-электроном. Тогда для молекулы LiH⁺ одноэлектронный гамильтониан Н можно записать в виде

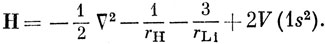
Если теперь перейти к молекуле LiH, то нужно включить еще потенциал, создаваемый вторым внешним электроном. Однако, пока не найдена соответствующая МО, этот потенциал не известен. Поэтому необходимо провести последовательный циклический расчет, приняв сначала МО в некотором, весьма грубом приближении и вычисляя с ее помощью потенциал, создаваемый электроном на этой орбитали. Далее этот потенциал добавляют в гамильтониан (10.35) и находят соответствующие этому гамильтониану МО. Эти МО используют далее для получения более точного потенциала, и эту процедуру повторяют до тех пор, пока не будет достигнуто самосогласование: при таком расчете с потенциалом получатся орбитали, практически совпадающие с теми, с помощью которых был построен сам потенциал. Такого рода расчеты аналогичны расчетам атома по методу ССП, описанному в гл. 4.

Теперь выполним для молекулы LiH то, что можно было бы назвать первым циклом в расчете по методу ССП. Допустим, что низшая МО (отличная от орбитали 1s_Li), на которую будут помещены два внешних электрона, распределена поровну между атомами, и электронную плотность на этой орбитали представим в виде

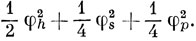
Несомненно, что такая орбиталь не может быть близка к искомой, так как водород имеет большую электроотрицательность, чем литий. Но мы располагаем, по крайней мере, некоторым приближением для начала вычислений.

Тогда гамильтониан равен

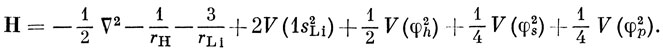
Рассмотрим, например, интеграл H_ss. Он разбивается на несколько слагаемых. Одно из них, равное

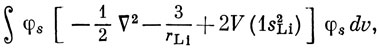
можно считать совпадающим с энергией 2s-орбитали атома лития. По данным спектроскопии, эта энергия составляет - 0,198 ат. ед. Оставшиеся члены содержат интегралы типа

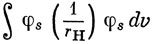
и ^*)

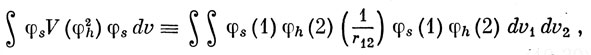
которые можно взять из работы Каро и Олсена. Следуя таким путем, находим значения интегралов, содержащих гамильтониан:

^*) (Потенциал, создаваемый электроном, находящимся на орбитали φ_h, равен

)

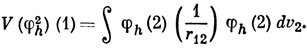
Уравнения для орбитальных коэффициентов молекулы имеют вид

и после умножения на -1 приходим к следующему вековому определителю:

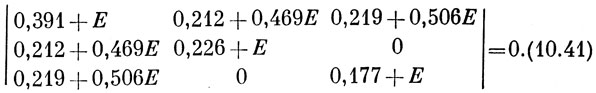
Раскрывая определитель (10.41), получим уравнение

которое имеет три корня: Е₁ = - 0,396; Е₂ = - 0,206; Е₃ = + 0,074.

Наименьший корень соответствует энергии низшей МО. Подставляя его в систему (10.40) и полагая для определенности c_h = 1, получим, что c_s = 0,153, с_р = 0,087. Ненормированная низшая МО, таким образом, имеет вид

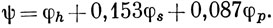
Нормировочный множитель равен

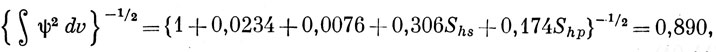
и окончательно

Итак, в результате расчета получилось, что около 80% электронной плотности приходится на 1s-орбиталь, что довольно сильно отличается от величины 50%, принятой в исходной функции при построении гамильтониана (10.36). Чтобы улучшить результаты расчета, орбиталь (10.45) надо использовать для получения более точного потенциала в гамильтониане (10.36). Каро и Олсен в результате самосогласованного расчета получили следующие отношения коэффициентов:

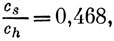
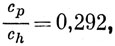
которые соответствуют орбитали

Взятое со знаком минус значение энергии, полученное при решении векового уравнения, можно приравнивать потенциалу ионизации электрона этой МО в предположении, что волновые функции остальных электронов при ионизации молекулы не изменяются (см. разд. 10.6). В нашем расчете потенциал ионизации молекулы LiH получается равным 10,8 эв. Самосогласованные вычисления Каро и Олсена дают 8,3 эв, что довольно хорошо согласуется с экспериментальным значением 8 эв.

Коэффициенты ЛКAO в методе МО непосредственно определяют меру ионности связи. Например, расчет молекулы LiH убедительно показывает, что избыток электронного заряда имеется на атоме водорода. Этот результат согласуется с химическими свойствами молекулы.

Если волновая функция молекулы представлена в виде произведения МО, антисимметризованного в соответствии с принципом Паули (7.5), то электронная плотность в молекуле вычисляется следующим образом:

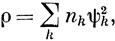
где n_k - число электронов, занимающих МО ψ_k (оно может быть равным 0, 1 или 2).

Для молекулы LiH при вычислении с МО [выражение (10.46)] получаем

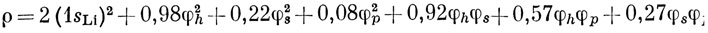
В выражении (10.48) содержатся плотности, соответствующие АО, например φ_h², и плотности перекрывания, например φ_hφ_р. Чтобы выяснить, как распределяется электронный заряд между двумя атомами, будем предполагать, что плотность перекрывания φ_aφ_b равна полусумме плотностей, соответствующих орбиталям φ_a и φ_b, умноженной на интеграл перекрывания, для того чтобы сохранялся суммарный электронный заряд ^*):

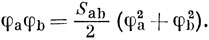
^*) (Суммарный заряд сохраняется, если обе части этого равенства проинтегрировать по всему пространству.)

Такая процедура позволяет получить величины, которые Малликен назвал полными атомными заселенностями; сумма их равна полному числу электронов в молекуле. Для молекулы LiH получаем следующие значения заселенностей:

Отсюда следует, что связь в молекуле LiH имеет ионный характер, который можно выразить формулой Li^+0,34 H^-0,34.

Дипольный момент системы точечных зарядов q_μ определяется в классической физике как

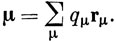
Если заряд распределен непрерывно с плотностью ρ, то

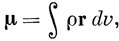
Молекулу можно характеризовать точечными зарядами Z_μe ядер и непрерывно распределенным электронным зарядом с плотностью, равной произведению квадрата модуля волновой функции на заряд электрона. Дипольный момент молекулы равен

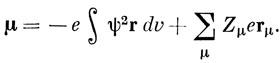
Для нейтральной молекулы дипольный момент, вычисленный по уравнению (10.51), не зависит от выбора начала координат векторов r; для заряженной молекулы это не так, и в этом случае начало координат обычно помещают в центр заряда.

В результате расчета молекулы LiH значение дипольного момента получается равным приблизительно 62). Следует отметить, что вычисление дипольного момента просто по заселенностям дает довольно плохие результаты, в особенности для небольших молекул; например, для молекулы LiH получается всего лишь 2,6 D. Одна из причин этого заключается в том, что плотности перекрывания φ_sφ_p вносят существенный вклад в дипольный момент, но не в заселенности, так как S_sp = 0.

На рис. 10.6 представлена корреляционная диаграмма для гетероядерной двухатомной молекулы, в которой электроотрицательность атома А больше, чем у атома В. Наиболее существенное отличие от корреляционной диаграммы (рис. 10.5) состоит в том, что для гетероядерных молекул в силу отсутствия классификации по g - u-состояниям вторая МО, которая в гомоядерной двухатомной молекуле является σ_u1s-орбиталью, коррелирует с 2s-орбиталью объединенного атома. В гетероядерных Молекулах отнесение орбитали к связывающему или разрыхляющему типу не обязательно такое же, как на корреляционной диаграмме гомоядерных молекул. Например, как уже было сказано, для молекулы LiH 2σ-орбиталь является связывающей, в то время как σ_u1s-орбиталь - всегда разрыхляющая.

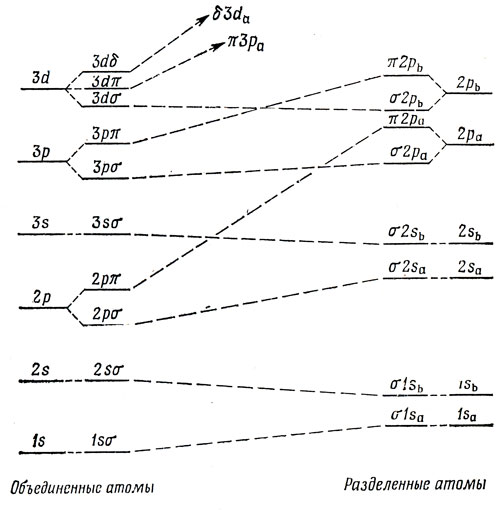
Рис. 10.6. Корреляционная диаграмма для орбиталей гетероядерной двухатомной молекулы

В некоторых случаях состояния гетероядерных двухатомных молекул можно рассматривать как возмущенные состояния изоэлектронных гомоядерных двухатомных молекул. Например, молекулы СО и N₂ в химическом отношении сильно различаются, но имеют довольно сходные схемы электронных состояний, как видно из табл. 10.3. Однако МО, полученные для молекулы СО по методу ССП, довольно сильно отличаются от орбиталей молекулы N₂. Это видно на примере связывающих π-орбиталей (см. [72]):

N2   ψ (πu2ρ) = 0,62 (2рπа + 2рπb), 
СО     ψ (1π) = 0,47 (2рπС) + 0,77 (2рπO).

Таблица 10.3. Сравнение некоторых электронных состояний молекул N₂ и СО (см. [61])