10.5. Правило непересечения

Корреляционная диаграмма (рис. 10.5) имеет одну особенность, которая требует пояснений. Откуда, например, следует, что σ_g2s-орбиталь коррелирует именно с 2s-орбиталью объединенного атома, а σ_g2р-орбиталь - с 3s-орбиталью? При построении корреляционной диаграммы учитывалась весьма общая теорема, касающаяся кривых электронной потенциальной энергии двухатомных молекул и известная как правило непересечения. Согласно этой теореме, потенциальные кривые двухатомной молекулы не могут пересекаться, если соответствующие электронные состояния обладают одинаковой симметрией.

Доказывается эта теорема следующим образом. Допустим, что при данном расстоянии между ядрами известны волновые функции всех электронных состояний молекулы, кроме двух, которые обозначаются Ψ₁ и Ψ₂. Пусть далее имеется полная система ортонормированных функций Θ, по которой можно разложить молекулярные волновые функции, и пусть функции Θ₁, Θ₂ из этой системы ортогональны ко всем известным волновым функциям Ψ и между собой. В таком случае функции Ψ₁ и Ψ₂ должны быть линейными комбинациями функций Θ₁ и Θ₂:

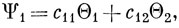
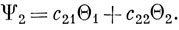
Чтобы найти энергии состояний Ψ₁ и Ψ₂, решаем вековое уравнение (6.68):

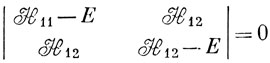
(здесь учтено, что S₁₁ = S₂₂ = 1, S₁₂ = 0).

Решения этого квадратного уравнения таковы:

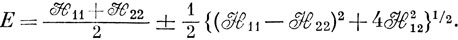
Корни векового уравнения равны между собой только в том случае, если одновременно H₁₁ - H₂₂ = 0 и H₁₂ = 0. Однако H₁₁ - H₂₂ и H₁₂ - независимые функции межъядерного расстояния, и маловероятно, чтобы при каком-либо расстоянии между ядрами они одновременно обращались в нуль. Поэтому, вообще говоря, два электронных состояния ни при каком межъядерном расстоянии не могут обладать одинаковыми энергиями, т. е. пересечение кривых потенциальной энергии не может иметь места. Однако, если H₁₂ = 0 при всех значениях межъядерного расстояния, как это наблюдается, когда функции Ψ₁ и Ψ₂ соответствуют состояниям с различной симметрией или разными спинами, может существовать такая точка, где H₁₁ - H₂₂ = 0. Поэтому кривые потенциальной энергии, соответствующие состояниям с различной симметрией или разными спинами, могут пересекаться.

Правило непересечения применимо как к электронным состояниям в целом (см. рис. 5.2 и 5.6), так и к молекулярным орбиталям. Применение этого правила к МО позволило построить однозначно корреляционные диаграммы, рассмотренные в этой главе.

Для многоатомных молекул правило непересечения значительно сложнее. Например, если положение ядер в молекуле определяется двумя координатами X и Y, то вместо кривых потенциальной энергии получаются потенциальные поверхности Е (X, Y), и если два состояния обладают одинаковой симметрией, то эти поверхности могут совпадать только в точке, но не на линии (см. [35]).