10.6. Более точные расчеты

Рассмотрим вкратце попытки, которые были сделаны для получения более точных волновых функций в рамках метода МО.

Простейшая функция, построенная для H₂⁺ в приближении МОЛКАО, дает энергию диссоциации 1,77 эв при равновесном расстоянии между протонами, равном 1,32 А. Оптимальный из расчетов приводит к энергии диссоциации 2,78 эв при равновесном расстоянии 1,06 А. Каковы основные пути улучшения расчетов?

Корреляционная диаграмма молекулярного иона H₂⁺ показывает, что сближение ядер приводит к уменьшению размеров σ_g1s-орбитали, так как показатель экспоненты для 1s-орбитали иона Не+ в два раза превосходит соответствующую величину для 1s-орбитали атома водорода. Поэтому лучшее приближение к σ_g1s-орбитали должно получаться, если брать ее в виде линейной комбинации 1s-орбиталей с варьируемым эффективным зарядом ядра:

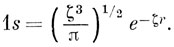
Коулсон [14], используя вариационный принцип для расчета с такой функцией, получил, что при равновесном расстоянии 1,06 А оптимальное значение ζ = 1,24, а соответствующая энергия диссоциации составляет 2,25 эв.

Другой эффект, который также следует принять во внимание, - это искажение каждым из протонов формы орбитали, отнесенной к другому протону. Это можно довольно хорошо учесть, включая 2pσ-орбитали в волновую функцию. Дикинсон [22] произвел расчет основного состояния иона H₂⁺ с функцией вида ^*)

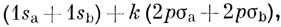
где функции 1s и 2рσ содержат вариационные параметры (эффективный ядерный заряд). Минимизируя энергию по отношению к значениям двух эффективных зарядов и коэффициента k, он нашел, что при равновесном расстоянии между ядрами ζ(1s) = 1,247, ζ(2р) ~ 1,868, k = 0,145. В этом расчете энергия диссоциации получилась равной 2,73 эв, что очень близко к значению, найденному в результате точного решения уравнения Шредингера для H₂⁺.

^*) (Принято говорить, что функция (10.53) учитывает поляризацию АО протоном. - Прим. перев.)

Можно получить точное решение электронного уравнения для молекулярного иона H₂⁺, не прибегая к методу МОЛКАО. Для этого переходят к эллиптическим координатам, в которых переменные уравнения разделяются. Эллиптические координаты вводятся следующим образом:

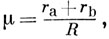
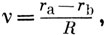
где r_а и r_b - расстояния от электрона до ядер а и b соответственно; φ - угол поворота вокруг оси молекулы. Решение волнового уравнения может быть получено в виде

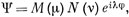
где М и N - функции, являющиеся решениями двух различных, но связанных между собой уравнений ^*).

^*) (Подробное рассмотрение решений этих уравнений содержится в работе [3].)

Вопрос о применении эллиптических координат для рассмотрения многоэлектронных двухатомных молекул был исследован в работе [32]. Основной недостаток такого подхода заключается в том, что его нельзя распространить на многоатомные молекулы в отличие от более грубого, но более гибкого приближения ЛКАО.

Если принять для молекулы H₂ волновую функцию, помещая два электрона с противоположными спинами на орбиталь

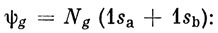
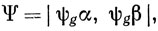
то вычисленная полная электронная энергия составляет 93% от экспериментального значения. Этот результат можно рассматривать как весьма удовлетворительный. Однако следует иметь в виду, что энергия диссоциации молекулы (а именно она представляет интерес в химии) значительно меньше полной электронной энергии. Вычисленная с такой простейшей волновой функцией энергия диссоциации молекулы Н₂ (2,65 эв) составляет лишь 55% от экспериментального значения (4,74 эв). Равновесное межъядерное расстояние также получается довольно плохим (0,85 А вместо экспериментального значения 0,74 А), и, следовательно, простая функция ЛКАО не очень хороша.

Если в качестве МО использовать функции, полученные по методу ССП, то вычисленное значение равновесного межъядерного расстояния (0,73 А) весьма близко к экспериментальному. Но энергия диссоциации (3,64 эв) все же далека еще от наблюдаемой на опыте [46]. Это означает, что для получения более точного значения энергии диссоциации необходимо выйти за рамки однодетерминантной формы волновой функции - шаг, который, как можно было убедиться, необходим также и в теории атома гелия. К этому вопросу мы еще вернемся в гл. 12.