10.7. Уравнения метода ССП и энергии МО

Понятие орбитали, несомненно, является самым полезным понятием в теории валентности. Все же трудно дать ему строгое математическое обоснование. Точнее говоря, орбиталь (как атомная, так и молекулярная) есть просто полезная одноэлектронная функция, удобная для построения многоэлектронных волновых функций. Она является собственной функцией одноэлектронного оператора, который можно определить в явном виде через координаты электронов и ядер системы. Однако если не используется приближение, в котором проводится усреднение энергии взаимодействия между электронами [см. выражение (4.2)], то этот одноэлектронный оператор не связан с полным гамильтонианом системы. Подобно этому энергию МО как собственное значение одноэлектронного оператора можно сопоставлять с экспериментальными значениями энергетических уровней системы лишь приближенно.

Как будет видно из гл. 12, отсутствие строгого определения МО имеет некоторые практические преимущества. Здесь же мы рассмотрим математическое обоснование понятия орбитали в методе ССП, так как среди различных типов орбиталей самосогласованная орбиталь определена наиболее точно и ее энергия наиболее тесно связана с экспериментальной энергией.

Пусть волновая функция системы, состоящей из n электронов, записана в виде простого произведения n спин-орбита лей [см. выражение (7.1)]:

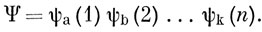
Вычислим с этой волновой функцией энергию

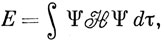
где H - полный электронный гамильтониан (в формуле 7.10 он обозначен H_е). Запишем H в виде

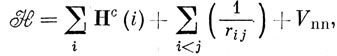
где Н^с (i) - так называемый гамильтониан остова, который состоит из оператора кинетической энергии и энергии притяжения i-го электрона к ядрам; V_nn - энергия отталкивания ядер.

Подставляя выражения (10.56) и (10.58) в выражение (10.57), легко видеть, что

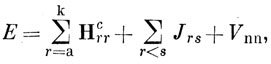
где

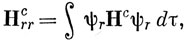
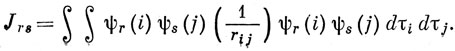
Выражение (10.59) состоит из двух частей: одна из них, в которую входит Н^с, представляет собой сумму энергий, которые имел бы каждый электрон в отсутствие остальных электронов; вторая часть есть полная энергия отталкивания всех электронов.

Волновая функция (10.56) не удовлетворяет требованию антисимметрии, но это легко исправить, используя вместо простого произведения слэтеровский определитель (7.6)

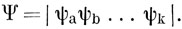
Считая спин-орбитали взаимно ортогональными и подставляя выражение (10.62) в выражение (10.57) (см. задачу 10.7), получим

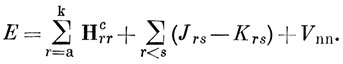
Последнее выражение отличается от выражения (10.59) появлением новых интегралов:

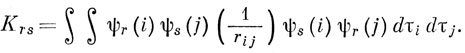
Интегралы, подобные J_rs и K_rs, встречались при вычислении энергии возбужденного состояния ³S атома гелия, с тем различием, что они содержат спин-орбитали, а не пространственные орбитали. J_rs называют кулоновским, a K_rs - обменным интегралом. Если ψ_r и ψ_s - спин-орбитали с различными спиновыми функциями (одна из них содержит спиновую функцию α, а другая - β), то, интегрируя по спиновым координатам, получаем, что значения K_rs равны нулю.

Применим теперь к функциям (10.56) или (10.62) вариационный принцип и выясним, при каких условиях энергии (10.58) и (10.63) минимальны. Эти условия достаточны для того, чтобы определить орбитали ψ, которые и называются самосогласованными орбиталями. Орбитали, найденные путем использования вариационного принципа для функции (10.56), называют орбиталями Хартри, а орбитали, полученные с учетом условия антисимметрии [см. выражение (10.62)], известны как орбитали Хартри - Фока, по имени создателей теории атомных орбиталей.

Для конфигурации, имеющей незамкнутую оболочку, однодетерминантная волновая функция не обязательно является хорошей волновой функцией. Например, для двух электронов, находящихся на различных орбиталях, возможны синглетное и триплетное состояния, причем синглетному состоянию соответствует волновая функция, являющаяся комбинацией двух определителей [см. выражение (9.47)]. В принципе самосогласованные орбитали можно построить для волновых функций любого другого типа, но математический расчет прост только для орбиталей Хартри и Хартри - Фока.

Выясним теперь, каким уравнениям удовлетворяют орбитали Хартри - Фока, так как они наиболее часто используются в современных расчетах. В дальнейшем в этой книге под самосогласованными орбиталями будут подразумеваться орбитали Хартри - Фока, если не делается специальной оговорки.

Предположим, что функция (10.62) не приводит к наименьшему значению энергии состояния. Тогда существует какая-то другая функция, например

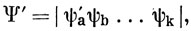
которой соответствует более низкая энергия. Допустим далее, что ψ_a' мало отличается от ψ_а и что она может быть записана в виде

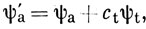
где ψ_t - спин-орбиталь, ортогональная ко всем функциям набора ψ_a ... ψ_k. Если c_t мало, то ψ_a' еще можно считать нормированной, так как нормировочная постоянная содержит только с_t². Используя соотношение (10.66), можно, очевидно, записать выражение (10.65) в виде

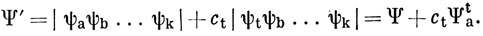
Другими словами, Ψ' получается путем добавки к Ψ малой примеси состояния Ψ_a^t, которое возникает при возбуждении электрона с орбитали ψ_а на орбиталь ψ_t.

Для того чтобы среди функций данного вида функция 4я была наилучшей (в энергетическом смысле), необходимо, чтобы c_t равнялось нулю. Отсюда следует [см. выражение (6.42)], что интеграл, вычисленный с гамильтониано и функциями Ψ и Ψ_а^t и обозначаемый F_at, должен равняться нулю:

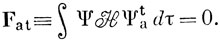
Если этот интеграл выразить через интегралы от спин-орбиталей (см. задачу 10.8), то получается

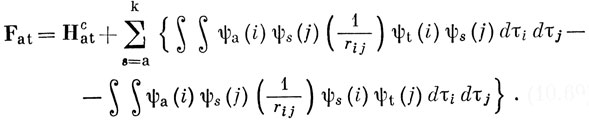
Чтобы выражение (10.69) обращалось в нуль для любых спин-орбиталей, необходимо, чтобы ψ были собственными функциями оператора F (см. задачу 6.1). Этот оператор несколько необычен, так как он зависит от своих собственных функций. Можно написать

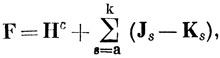
где J_s и K_s - кулоновский и обменный операторы, определяемые своими матричными элементами следующим образом:

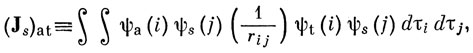
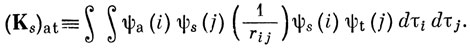
Заметим, что (J_s)_rr и (K_s)_rr есть интегралы J_rs и K_rs, определенные по выражениям (10.61) и (10.64), и что (J_a)_at = (K_a)_at.

Отметим, между прочим, что оператор, определяющий орбитали Хартри в методе ССП, не содержит обменного оператора K_s, а сумма по s не содержит слагаемого с s - а. Кроме того, уравнения характеризуют лишь пространственную часть спин-орбитали; спиновая же ее часть (α или β) определяется первоначальным выбором волновой функции.

Поэтому в методе ССП потенциал, определяющий МО, содержит потенциал остова, кулоновский потенциал всех электронов и обменный потенциал для каждого электрона. Поскольку кулоновский и обменный потенциалы сами зависят от орбиталей, для отыскания самосогласованных орбиталей приходится, как указывалось выше, применять метод итераций. Самосогласование считается достигнутым, если с найденными орбиталями получается тот потенциал, с помощью которого они были определены.

Собственные значения оператора F можно назвать орбитальными энергиями. Из выражения (10.69) следует, что

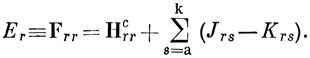
Сумма энергий всех занятых спин-орбиталей равна

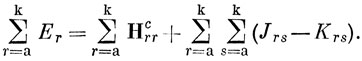
Поскольку J_rr = К_rr, получаем

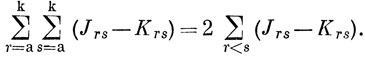
Учитывая уравнение (10.74) и сравнивая уравнение (10.73) с выражением (10.63), имеем

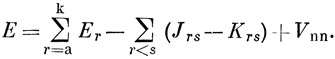
Таким образом, для самосогласованных орбиталей полная электронная энергия не является просто суммой орбитальных энергий и энергии отталкивания ядер.

Допустим теперь, что электрон удален со спин-орбитали ψ_a, причем волновые функции других электронов остались неизменными. Тогда энергия положительного иона, волновая функция которого имеет вид

равна, согласно выражению (10.63),

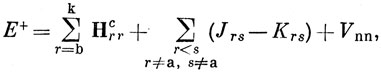
а из выражения (10.72) очевидно, что

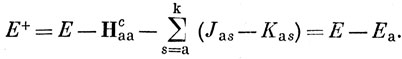
Отсюда следует, что - Е_а можно приравнивать к потенциалу ионизации (Е⁺ - Е), который представляет собой энергию, необходимую для ионизации молекулы, если процесс ионизации рассматривать как отрыв электронов с орбитали без изменения волновых функций остальных электронов. Этот результат известен под названием теоремы Купмена.

Важным частным случаем являются орбитали, полученные по методу ССП для конфигурации с заполненной оболочкой, когда каждая орбиталь занята двумя электронами со спиновыми функциями α и β. В этом случае вместо выражений (10.63), (10.69) и (10.72) имеем

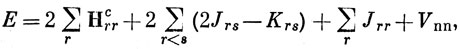
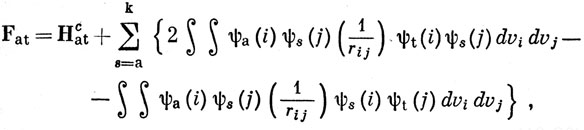
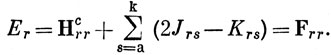
Суммирование здесь проводится по всем занятым орбиталям, а не спин-орбиталям.

Если для построения самосогласованных орбиталей используется приближение ЛКАО

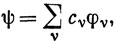
то, подставляя выражение (10.82) в уравнение (10.80) и выделяя коэффициенты при c_aμc_tν, получим

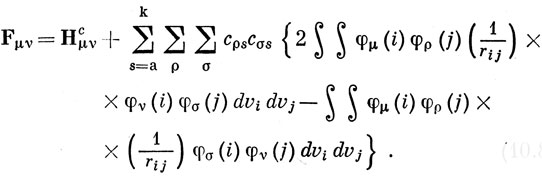
Самосогласованные орбитали для системы с заполненном оболочкой определяются тогда путем решения уравнений

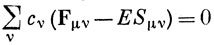
при условии, что определитель системы равен нулю:

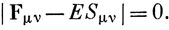
Эти уравнения известны как уравнения Рутана. Для решения уравнений (10.84) также приходится применять метод итераций, так как эти уравнения являются кубическими относительно коэффициентов c_ν [величины F_μν квадратично зависят от них, см. уравнение (10.83)].

Мы вернемся к уравнениям Рутана в гл. 15 ^*).

^*) (В работе [75] в связи с применением к молекуле N₂ метода ССП в приближении МОЛКАО имеется полезный обзор расчетов двухатомных молекул по методу Рутана.)